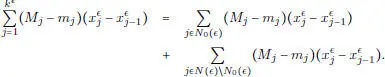
Pero, para cada j  N \ N 0(
N \ N 0(  ), se tiene M j–m j < 1/ p ; para j
), se tiene M j–m j < 1/ p ; para j  N 0(
N 0(  ),
), 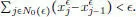 En consecuencia, se obtiene:
En consecuencia, se obtiene:
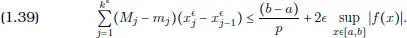
La desigualdad (1.39) y (1.24) nos permiten concluir, ya que  y p pueden ser escogidos arbitrariamente.
y p pueden ser escogidos arbitrariamente.
Por último, para probar que D f es de extensión nula si y sólo si cada E p lo es, se deja al lector el ejercicio de verificar las dos aserciones siguientes:
 Todo subconjunto de un conjunto de extensión nula es de extensión nula;
Todo subconjunto de un conjunto de extensión nula es de extensión nula;
 Toda reunión numerable de conjuntos de extensión nula es de extensión nula.
Toda reunión numerable de conjuntos de extensión nula es de extensión nula.

4. La integral de funciones con valores complejos
La integral de Riemann admite una extensión inmediata al caso de funciones complejas. Si f es una función definida en un intervalo [ a , b ] de 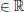 , con valores complejos, le asociamos dos funciones reales: su parte real
, con valores complejos, le asociamos dos funciones reales: su parte real 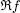 y su parte imaginaria
y su parte imaginaria 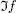 , que permiten representarla
, que permiten representarla
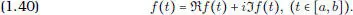
DEFINICIÓN 1.4. Una función f : [ a , b ] →  es integrable en el sentido de Riemann si
es integrable en el sentido de Riemann si 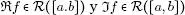 . Su integral es entonces
. Su integral es entonces
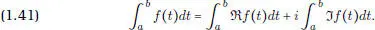
Llamamos 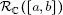 el conjunto de tales funciones f .
el conjunto de tales funciones f .
PROPOSICIÓN 1.1. Si f es una Junción en 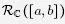 , su integral satisface la desigualdad
, su integral satisface la desigualdad
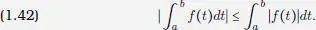
Demostración. Sean 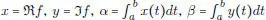 . Entonces:
. Entonces:
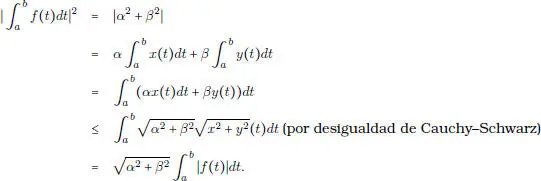

En un ejercicio al fin del capítulo estudiaremos en qué caso se tiene la igualdad en (1.42).
5. Comentarios
Observemos que los tres procedimientos del “arte de medir” analizados en este capítulo: cálculo de sumas de series, cálculo de superficies, integración en el sentido de Riemann, descansan en propiedades básicas relativamente simples.
En primer lugar, hemos visto que los conjuntos que pueden ser medidos, satisfacen ciertas propiedades con respecto a las operaciones usuales sobre conjuntos. Lo mínimo necesario corresponde a la estabilidad para reuniones e intersecciones finitas (por ejemplo, la reunión finita de conjuntos con superficie posee superficie).
En segundo lugar, la aplicación que mide los conjuntos debe ser creciente, en el sentido de la inclusión de conjuntos: si un conjunto con superficie contiene a otro, la superficie del primero es mayor que la del segundo.
En tercer lugar, es necesario establecer una regla para medir una reunión finita de conjuntos (ver (S2)).
Finalmente, es necesario un “buen comportamiento” con respecto a límites crecientes y decrecientes de conjuntos. Estas últimas son propiedades llamadas de continuidad inferior y superior cuyo sentido riguroso se estudiará más tarde, (ver (S4) y el ejercicio 1.3).
Estas ideas básicas nos acompañarán a lo largo de este volumen: constituyen los pilares de la teoría de capacidades y de la medida. Respecto a la primera, la teoría de capacidades, que no constituye requisito para los cursos básicos de Análisis e Integración, hemos reservado un capítulo anexo al final del libro para quienes deseen tener una introducción al tema.
Para el lector interesado en seguir el desarrollo histórico de la teoría de la integración, se recomienda la lectura del excelente libro de Pesin [ 39], que pasa en revista los pasos dados en su formalización.
6. Ejercicios propuestos
1. Sea f una función continua definida sobre el intervalo compacto real [ a , b ] y con valores en 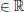 .
.
a) Se supone f positiva y 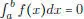 . Probar que f es nula.
. Probar que f es nula.
b) Se supone que para todo n  , la integral
, la integral 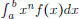 es nula. Probar que f es nula.
es nula. Probar que f es nula.
Читать дальше

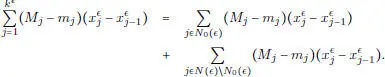
 N \ N 0(
N \ N 0( 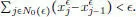 En consecuencia, se obtiene:
En consecuencia, se obtiene: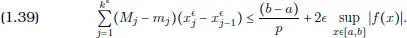
 Todo subconjunto de un conjunto de extensión nula es de extensión nula;
Todo subconjunto de un conjunto de extensión nula es de extensión nula;
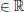 , con valores complejos, le asociamos dos funciones reales: su parte real
, con valores complejos, le asociamos dos funciones reales: su parte real 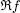 y su parte imaginaria
y su parte imaginaria 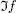 , que permiten representarla
, que permiten representarla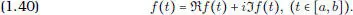
 es integrable en el sentido de Riemann si
es integrable en el sentido de Riemann si 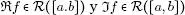 . Su integral es entonces
. Su integral es entonces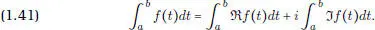
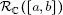 el conjunto de tales funciones f .
el conjunto de tales funciones f .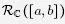 , su integral satisface la desigualdad
, su integral satisface la desigualdad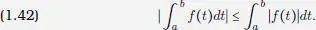
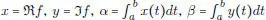 . Entonces:
. Entonces: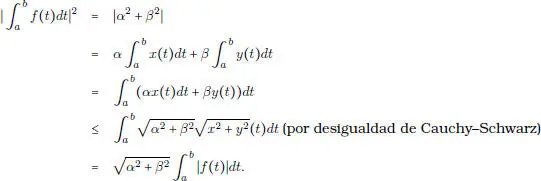
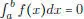 . Probar que f es nula.
. Probar que f es nula. , la integral
, la integral 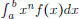 es nula. Probar que f es nula.
es nula. Probar que f es nula.










