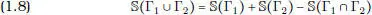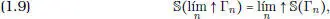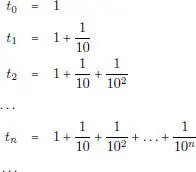
y aprovechando nuestros conocimientos sobre series podemos enfrentar el argumento falaz de Zenón.
La teoría de series comenzó a desarrollarse a fines del siglo XVII y principios del XVIII, sin contar con un adecuado concepto de límite. Esto fue causa de muchas paradojas. Por ejemplo, aquellas sobre la suma de la serie

Esta “suma infinita” se puede escribir
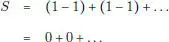
de modo que S = 0. Pero, agrupando los términos de otro modo, se tiene
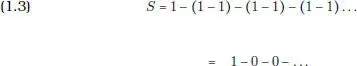
luego S = 1, o incluso, según (1.3), S = 1 – S , ¡y en consecuencia S = 1/2!
Sin embargo, la teoría de series permitía abordar de manera “primaria” la Mecánica de Newton que entonces daba sus primeros pasos. Veamos cómo.
Nos interesa estudiar el movimiento de un punto material de masa m sobre la recta real  . Llamemos X tla posición del móvil en el instante t . Suponemos que el tiempo se mide sobre los enteros positivos. Supongamos que el móvil parte desde un punto inicial x
. Llamemos X tla posición del móvil en el instante t . Suponemos que el tiempo se mide sobre los enteros positivos. Supongamos que el móvil parte desde un punto inicial x  , en presencia de una fuerza constante F en el sentido positivo del eje de coordenadas espaciales. Para simplificar aún más, despreciamos primero toda fuerza de roce. Según la segunda Ley de Newton, la fuerza es proporcional a la aceleración A tque alcanzará el punto material en su movimiento. En este caso entonces,
, en presencia de una fuerza constante F en el sentido positivo del eje de coordenadas espaciales. Para simplificar aún más, despreciamos primero toda fuerza de roce. Según la segunda Ley de Newton, la fuerza es proporcional a la aceleración A tque alcanzará el punto material en su movimiento. En este caso entonces, 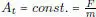 . Llamemos V tla velocidad del móvil, e introduzcamos el símbolo Δ para indicar diferencias, vale decir Δ X t = X t – X t–1. Se tiene entonces que
. Llamemos V tla velocidad del móvil, e introduzcamos el símbolo Δ para indicar diferencias, vale decir Δ X t = X t – X t–1. Se tiene entonces que 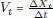 y
y 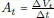 , donde Δ t es, por supuesto, igual a 1. Ahora bien, ya que la aceleración es constante, se tiene que X t satisface la ecuación
, donde Δ t es, por supuesto, igual a 1. Ahora bien, ya que la aceleración es constante, se tiene que X t satisface la ecuación

En este caso, es muy sencillo calcular la expresión que tiene la solución de (1.4). En efecto, basta aplicar la fórmula (1.1):
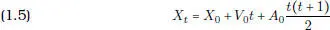
El lector reconocerá la versión en tiempo discreto de la clásica fórmula

que se obtiene en Mecánica Clásica resolviendo una ecuación diferencial . En efecto, toda esta coincidencia es absolutamente natural, tanto (1.5) como (1.6) expresan la acción de medir: en el primer caso, se mide mediante una suma; en el segundo, mediante una integral.
2. Superficies en el plano
El cálculo de superficies en el plano es quizás una de las formas más intuitivas del arte de medir. Aprovecharemos esa intuición para construir un modelo matemático de la noción de superficie.
2.1. Noción de superficie.Nuestro propósito es definir una noción de superficie (o área) de una parte del plano. Con este fin se provee al plano de ejes de coordenadas ortogonales y se atribuye la superficie 1 al cuadrado de lado unitario. Las hipótesis siguientes traducen nuestras intuiciones básicas sobre superficies:
(S1) Hipótesis 1: La superficie 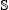 (Γ) de una parte Γ del plano es, si ella existe, un número positivo.
(Γ) de una parte Γ del plano es, si ella existe, un número positivo.
(S2) Hipótesis 2: Si Γ y Γ′ son partes del plano que poseen superficie, entonces también es así para Γ ∩ Γ′ y
Γ ∪ Γ′. Si además Γ y Γ′ son disjuntos, se tiene

Si Γ contiene a Γ′, entonces su diferencia Γ\Γ′ tiene una superficie que vale 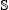 (Γ) –
(Γ) – 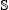 (Γ′).
(Γ′).
(S3) Hipótesis 3: Si r tiene una superficie nula, entonces todo subconjunto de r posee también una superficie (que además es nula a causa de lo que se vio en (S2)).
EJERCICIO 1.1. Probar que si Γ y Γ 2son dos conjuntos que poseen una superficie, entonces por (S2) siempre se tiene
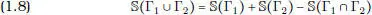
Ahora bien, recordemos la forma en que los griegos aproximaban la superficie de un círculo: se daban una sucesión de polígonos regulares inscritos en él, calculaban las respectivas superficies y luego “pasaban al límite”. Expresemos esta idea en una nueva hipótesis, introduciendo sobre los conjuntos el orden parcial asociado a la inclusión.
(S4) Hipótesis 4: Si (Γ n) nes una sucesión creciente de conjuntos que tienen superficie, entonces su reunión ∪ nΓ n(que también escribimos lím ↑ Γ n) tiene una superficie si y sólo si la sucesión ( 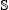 (Γ n)) nes acotada y en tal caso se tiene
(Γ n)) nes acotada y en tal caso se tiene
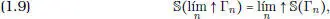
EJERCICIO 1.2. Probar que (S4) es equivalente a la propiedad siguiente (S4’) Si (Γ n) nes una sucesión de conjuntos que poseen superficie, disjuntos dos a dos, entonces su reunión Γ (que escribimos Γ = ∑ nΓ n), tiene superficie si y sólo si la serie ∑ n 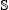 (Γ n) converge; y se tiene:
(Γ n) converge; y se tiene:
Читать дальше

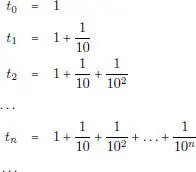

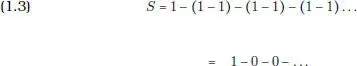
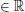 . Llamemos X tla posición del móvil en el instante t . Suponemos que el tiempo se mide sobre los enteros positivos. Supongamos que el móvil parte desde un punto inicial x
. Llamemos X tla posición del móvil en el instante t . Suponemos que el tiempo se mide sobre los enteros positivos. Supongamos que el móvil parte desde un punto inicial x  , en presencia de una fuerza constante F en el sentido positivo del eje de coordenadas espaciales. Para simplificar aún más, despreciamos primero toda fuerza de roce. Según la segunda Ley de Newton, la fuerza es proporcional a la aceleración A tque alcanzará el punto material en su movimiento. En este caso entonces,
, en presencia de una fuerza constante F en el sentido positivo del eje de coordenadas espaciales. Para simplificar aún más, despreciamos primero toda fuerza de roce. Según la segunda Ley de Newton, la fuerza es proporcional a la aceleración A tque alcanzará el punto material en su movimiento. En este caso entonces, 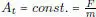 . Llamemos V tla velocidad del móvil, e introduzcamos el símbolo Δ para indicar diferencias, vale decir Δ X t = X t – X t–1. Se tiene entonces que
. Llamemos V tla velocidad del móvil, e introduzcamos el símbolo Δ para indicar diferencias, vale decir Δ X t = X t – X t–1. Se tiene entonces que 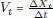 y
y 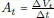 , donde Δ t es, por supuesto, igual a 1. Ahora bien, ya que la aceleración es constante, se tiene que X t satisface la ecuación
, donde Δ t es, por supuesto, igual a 1. Ahora bien, ya que la aceleración es constante, se tiene que X t satisface la ecuación
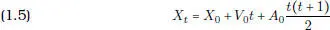

 (Γ) de una parte Γ del plano es, si ella existe, un número positivo.
(Γ) de una parte Γ del plano es, si ella existe, un número positivo.