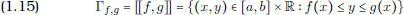EJERCICIO 1.3. Sea (Γ n) nuna sucesión decreciente de conjuntos que poseen superficie y sea Γ = ∩ nΓ n(que también escribimos lím n↓ Γ n). Probar que (Γ 0\Γ n) ncrece hacia Γ 0\Γ. Deducir que r tiene superficie y verificar que

EJERCICIO 1.4. Consideremos ahora un conjunto Γ para el cual existen dos sucesiones de conjuntos que poseen superficie, 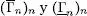 tales que
tales que
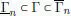
para todo n  . Si la sucesión
. Si la sucesión 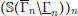 tiende a cero, entonces Γ tiene superficie y se cumple
tiende a cero, entonces Γ tiene superficie y se cumple
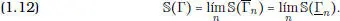
(Se recomienda considerar las sucesiones monótonas 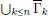 (decreciente) y
(decreciente) y 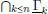 (creciente) de límites
(creciente) de límites  y
y  , respectivamente, que tienen la misma superficie. Luego, observar que Γ\
, respectivamente, que tienen la misma superficie. Luego, observar que Γ\  está contenido en el conjunto de superficie nula
está contenido en el conjunto de superficie nula  \
\  ).
).
En el ejercicio siguiente pasamos en revista lo aprendido en los cursos de Geometría elemental.
EJERCICIO 1.5.
1. Probar que la superficie de un rectángulo es el producto de sus lados.
2. Probar que un segmento de recta tiene superficie nula. Asimismo, demostrar que una recta tiene superficie nula.
3. Probar que una banda de plano limitada por dos rectas paralelas no tiene superficie.
4. Probar que un conjunto numerable de puntos del plano tiene superficie nula.
5. calcular la superficie de un triángulo rectángulo usando el ejercicio 1.4 y la pregunta 1 aquí arriba.
6. Calcular la superficie de un paralelógramo en el plano, ubicado de modo que uno de sus vértices se encuentre en el origen de coordenadas, pero sin lados paralelos a los ejes.
7. Obtener la superficie de un círculo como límite de las superficies de polígonos regulares inscritos y exinscritos de n lados.
3. La integral de Riemann
Demos una rápida mirada a la forma en que se define la integral de Riemann en los cursos elementales de cálculo, buscando extraer de esa construcción los elementos comunes con el cálculo de superficies en el plano y con el arte de sumar.
DEFINICIÓN 1.1. Designamos por ɛ ( I ) el conjunto de las funciones escalonadas definidas sobre un intervalo I = [ a , b ] ( a < b ) de la recta real. Una función f es escalonada si existe una partición a = x 0< x 1< ... < x n= b tal que f restringida a cada subintervalo [ x k , x k+1[, k = 0,..., n – 2; [ x n–1, x n] sea constante.
Consideremos una función f  ɛ ( I ) y la figura Γ delimitada por los segmentos de rectas
ɛ ( I ) y la figura Γ delimitada por los segmentos de rectas  , k = l,..., n – 1. Γes una unión de rectángulos no traslapados. Podemos entonces definir su área como la suma de las áreas de tales rectángulos elementales, de modo que:
, k = l,..., n – 1. Γes una unión de rectángulos no traslapados. Podemos entonces definir su área como la suma de las áreas de tales rectángulos elementales, de modo que:
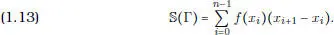
Llamemos a esta cantidad, integral de la función escalonada f sobre el intervalo I = [ a , b ]. La denotamos 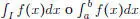 .
.
EJERCICIO 1.6. Probar que para todo par de funciones f , g  ɛ ( I ) se tiene que αf + βg
ɛ ( I ) se tiene que αf + βg  ɛ ( I ) para todo par de reales α, β y que se cumple
ɛ ( I ) para todo par de reales α, β y que se cumple
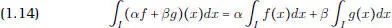
Resumimos lo anterior diciendo que ɛ ( I ) es un espacio vectorial real y que la aplicación f ↦ ∫ If ( x ) dx es una forma lineal sobre este espacio.
OBSERVACIÓN 1.1. Sean f y g dos funciones reales definidas sobre un intervalo [ a , b ] de  y tales que en todo punto x
y tales que en todo punto x  [ a , b ] se tenga f ( x ) ≤ g ( x ). Definimos:
[ a , b ] se tenga f ( x ) ≤ g ( x ). Definimos:
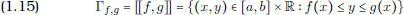
La notación [[ f , g ]] sugiere una analogía con los intervalos de 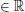 . En particular se puede notar que si una sucesión de funciones positivas ( f n ) ndefinidas en [ a , b ] es tal que en cada punto x del dominio f n ( x ) crece o decrece hacia f ( x ), entonces [[0, f n ]] tiene como límite [[0, f ]]. Dicho de otro modo,
. En particular se puede notar que si una sucesión de funciones positivas ( f n ) ndefinidas en [ a , b ] es tal que en cada punto x del dominio f n ( x ) crece o decrece hacia f ( x ), entonces [[0, f n ]] tiene como límite [[0, f ]]. Dicho de otro modo,
Читать дальше



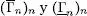 tales que
tales que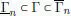
 . Si la sucesión
. Si la sucesión 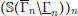 tiende a cero, entonces Γ tiene superficie y se cumple
tiende a cero, entonces Γ tiene superficie y se cumple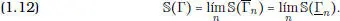
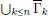 (decreciente) y
(decreciente) y 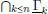 (creciente) de límites
(creciente) de límites  y
y  , respectivamente, que tienen la misma superficie. Luego, observar que Γ\
, respectivamente, que tienen la misma superficie. Luego, observar que Γ\  ɛ ( I ) y la figura Γ delimitada por los segmentos de rectas
ɛ ( I ) y la figura Γ delimitada por los segmentos de rectas  , k = l,..., n – 1. Γes una unión de rectángulos no traslapados. Podemos entonces definir su área como la suma de las áreas de tales rectángulos elementales, de modo que:
, k = l,..., n – 1. Γes una unión de rectángulos no traslapados. Podemos entonces definir su área como la suma de las áreas de tales rectángulos elementales, de modo que: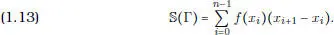
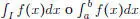 .
.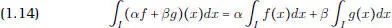
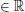 y tales que en todo punto x
y tales que en todo punto x