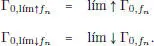
Notar que si f es una función escalonada positiva, entonces

Si f es una función real de signo cualquiera, introduzcamos las siguientes funciones asociadas:
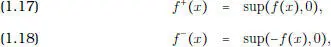
para todo x en el respectivo dominio de definición. Se puede observar que
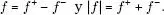
Para una función escalonada f cualquiera se verifica entonces:
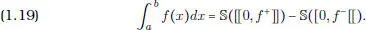
Y si g es otra función escalonada tal que f ≤ g , entonces:
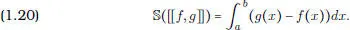
DEFINICIÓN 1.2. Sea f una función de [ a , b ] en 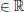 . Decimos que ella es integrable en el sentido de Riemann si existe
. Decimos que ella es integrable en el sentido de Riemann si existe
 una sucesión decreciente
una sucesión decreciente 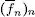 de funciones escalonadas en [ a , b ] minoradas por f ,
de funciones escalonadas en [ a , b ] minoradas por f ,
 una sucesión creciente
una sucesión creciente 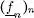 de funciones escalonadas mayoradas por f , tales que
de funciones escalonadas mayoradas por f , tales que
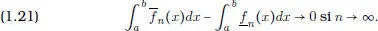
En tal caso, el límite común de las sucesiones 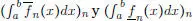 se escribe
se escribe 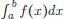 , recibiendo el nombre de integral de f sobre [ a , b ].
, recibiendo el nombre de integral de f sobre [ a , b ].
Notar que si f es positiva y si escribimos 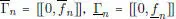 , entonces la condición (1.21) equivale a la planteada en el ejercicio 1.4.
, entonces la condición (1.21) equivale a la planteada en el ejercicio 1.4.
Puesto que las funciones escalonadas son acotadas sobre todo intervalo acotado [ a , b ], las funciones integrables en ese intervalo también lo son. Una elección posible de las sucesiones 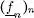 y
y 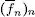 es la propuesta por Darboux que explicamos a continuación. Sea ( π ( n )) nuna sucesión de particiones de [ a , b ], π ( n ) :
es la propuesta por Darboux que explicamos a continuación. Sea ( π ( n )) nuna sucesión de particiones de [ a , b ], π ( n ) : 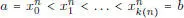 , llamamos
, llamamos 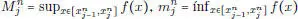 para cada j = 1,..., k ( n ). Definimos entonces, para cada n
para cada j = 1,..., k ( n ). Definimos entonces, para cada n  ,
,
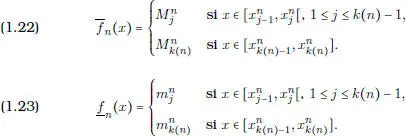
De este modo se tiene
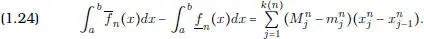
De (1.22), (1.23), (1.24), resulta una forma equivalente de definir la integrabilidad en el sentido de Riemann: una función f acotada es integrable si y sólo si las sumas del miembro derecho de (1.24) convergen a 0 si n → ∞.
EJERCICIO 1.7. Probar que toda función real continua es integrable sobre todo intervalo acotado contenido en su dominio de definición.
EJERCICIO 1.8. Sea f una función real integrable en el sentido de Riemann sobre [ a , b ] y sea g otra función real, que es igual a f salvo en un número finito de puntos. Probar que g es también integrable en el sentido de Riemann y que su integral coincide con la de f .
Deducir en particular que toda función continua, salvo en un número finito de puntos sobre [ a , b ], es integrable.
EJERCICIO 1.9. Probar que la función f definida sobre [0,1], que vale 1 sobre los puntos racionales y 0 en todos los otros, no es integrable en el sentido de Riemann. Sin embargo, el conjunto [[0, f ]] tiene superficie nula.
En el teorema siguiente resumimos las propiedades esenciales de la Integral de Riemann estudiadas en los cursos elementales de Cálculo.
TEOREMA 1.1. Dado un intervalo I = [ a , b ] de la recta real, designemos por R ( I ) el conjunto de las funciones reales que son integrables en el sentido de Riemann sobre I .
1. R ( I ) es un espacio vectorial real y la aplicación f ↦ ∫ I f ( x ) dx es una forma lineal definida sobre este espacio.
2. La forma lineal anterior es también creciente sobre R ( I ), vale decir: f ≤ g implica ∫ I f ( x ) dx ≤ ∫ I g ( x ) dx .
3. R ( I ) es también estable para el producto de funciones y para las operaciones ( f , g ) ↦ sup( f , g ), ( f , g ) ↦ ínf( f , g ).
4. f  R ( I ) si y sólo si f +
R ( I ) si y sólo si f +  R ( I ) y f –
R ( I ) y f –  R ( I ). En tal caso se tiene:
R ( I ). En tal caso se tiene:
Читать дальше

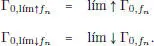

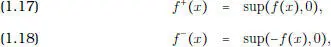
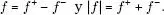
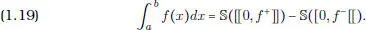
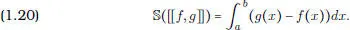
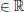 . Decimos que ella es integrable en el sentido de Riemann si existe
. Decimos que ella es integrable en el sentido de Riemann si existe una sucesión decreciente
una sucesión decreciente 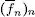 de funciones escalonadas en [ a , b ] minoradas por f ,
de funciones escalonadas en [ a , b ] minoradas por f ,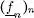 de funciones escalonadas mayoradas por f , tales que
de funciones escalonadas mayoradas por f , tales que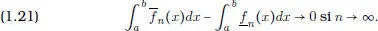
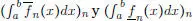 se escribe
se escribe 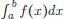 , recibiendo el nombre de integral de f sobre [ a , b ].
, recibiendo el nombre de integral de f sobre [ a , b ].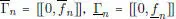 , entonces la condición (1.21) equivale a la planteada en el ejercicio 1.4.
, entonces la condición (1.21) equivale a la planteada en el ejercicio 1.4.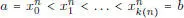 , llamamos
, llamamos 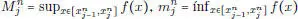 para cada j = 1,..., k ( n ). Definimos entonces, para cada n
para cada j = 1,..., k ( n ). Definimos entonces, para cada n  ,
,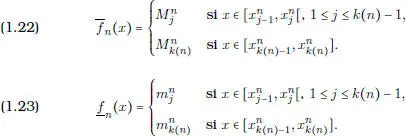
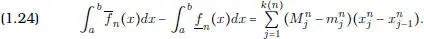
 R ( I ) si y sólo si f +
R ( I ) si y sólo si f + 










