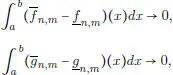
si m → ∞. Además se pueden escoger estas funciones escalonadas de modo que 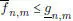 , si es necesario reemplazando
, si es necesario reemplazando 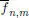 por ínf
por ínf 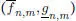 y
y 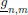 por sup
por sup 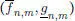 . Entonces,
. Entonces,
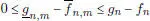
para todo n  . Tomando enseguida las sucesiones diagonales
. Tomando enseguida las sucesiones diagonales 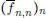 y
y 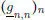 se tiene que ellas son aproximantes de f en el sentido de la definición de la integral de Riemann y
se tiene que ellas son aproximantes de f en el sentido de la definición de la integral de Riemann y 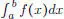 es igual al límite común de las integrales de tales funciones escalonadas. Pero además por construcción de las sucesiones de funciones escalonadas, los límites de sus integrales deben coincidir con los de la ecuación (1.34).
es igual al límite común de las integrales de tales funciones escalonadas. Pero además por construcción de las sucesiones de funciones escalonadas, los límites de sus integrales deben coincidir con los de la ecuación (1.34).
Una vez demostrada esta propiedad, el teorema de cambio de variables resulta por una aplicación directa de ella y del cambio de variables para funciones escalonadas.
Asimismo, la prueba de la última parte del teorema se obtiene por aplicación de (1.34): la superficie de la figura comprendida entre dos funciones escalonadas se expresa claramente como la integral de su diferencia; en el caso general, la aproximación por funciones escalonadas provee el resultado usando (1.34).

Nos preguntamos ahora qué tan extensa puede ser la clase de las funciones integrables en el sentido de Riemann. Sabemos que contiene a las funciones continuas salvo en un número finito de puntos, pero, ¿qué tanto más podemos relajar la condición de continuidad? Este problema fue planteado y resuelto por Du Bois-Reymond en 1882.
DEFINICIÓN 1.3. Un subconjunto N de la recta real se dice de extensión nula (más tarde diremos de medida nula ) si para cada  > 0 existe una colección finita de intervalos
> 0 existe una colección finita de intervalos 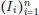 cuyo largo total (calculado como la suma de las longitudes respectivas) sea menor que e y su reunión cubre a N .
cuyo largo total (calculado como la suma de las longitudes respectivas) sea menor que e y su reunión cubre a N .
TEOREMA 1.2. Sea f una función con valores reales definida en un intervalo [ a , b ] de  y acotada. Ella es integrable en el sentido de Riemann sobre [ a , b ] si y sólo si su conjunto de discontinuidades D fes de extensión nula.
y acotada. Ella es integrable en el sentido de Riemann sobre [ a , b ] si y sólo si su conjunto de discontinuidades D fes de extensión nula.
Demostración. Designemos por ω ( f , E ) la oscilación de f sobre un subconjunto E de [ a , b ] dada por la expresión
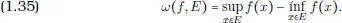
Observar que ω ( f , E ) ≤ ω ( f , E′ ) si E ⊂ E′ . Así, la oscilación de f en un punto x  [ a , b ] es
[ a , b ] es
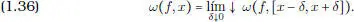
Claramente f es continua en x si y sólo si ω ( f , x ) = 0. Entonces D f se escribe en la forma
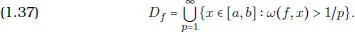
Comenzaremos por probar que f es integrable sobre [ a , b ] si y sólo si para cada p ≥ 1 el conjunto E p= { x  [ a , b ] : ω ( f , x ) > 1/ p } es de extensión nula.
[ a , b ] : ω ( f , x ) > 1/ p } es de extensión nula.
Supongamos f  R ([ a , b ]). Sea ( π ( n )) nuna sucesión de particiones de [ a , b ], π ( n ) :
R ([ a , b ]). Sea ( π ( n )) nuna sucesión de particiones de [ a , b ], π ( n ) : 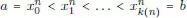 . Examinemos (1.24). Dado p > 1, E pqueda contenido en los intervalos de la partición π ( n ) en los cuales la oscilación
. Examinemos (1.24). Dado p > 1, E pqueda contenido en los intervalos de la partición π ( n ) en los cuales la oscilación  es mayor que 1/ p . Llamemos l n ( p ) la suma de las longitudes de dichos intervalos. Se tiene entonces
es mayor que 1/ p . Llamemos l n ( p ) la suma de las longitudes de dichos intervalos. Se tiene entonces
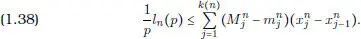
y la integrabilidad de f determina la convergencia a 0 de las sumas de (1.38) si n → ∞, de donde, para cada p fijo, l n( p ) → 0. Esta última propiedad nos dice que E p es de extensión nula para cada p ≥ 1.
Recíprocamente, supongamos E p de extensión nula para cada p > 1. Entonces, dado  > 0 existe una colección finita de intervalos
> 0 existe una colección finita de intervalos  que cubren E p y cuya suma de longitudes es menor que
que cubren E p y cuya suma de longitudes es menor que  . Dada una partición cualquiera π de [ a , b ], designemos por I 1,..., I klos subintervalos disjuntos de [ a , b ] que ella determina. Refinemos π de la siguiente manera: llamemos π la partición definida por las extremidades de los intervalos que resultan al considerarlos de la forma I y las intersecciones de aquellos con los de la forma J . De esa manera, la partición π contiene intervalos
. Dada una partición cualquiera π de [ a , b ], designemos por I 1,..., I klos subintervalos disjuntos de [ a , b ] que ella determina. Refinemos π de la siguiente manera: llamemos π la partición definida por las extremidades de los intervalos que resultan al considerarlos de la forma I y las intersecciones de aquellos con los de la forma J . De esa manera, la partición π contiene intervalos 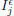 de extremidades
de extremidades 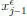 y
y 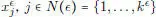 , entre los cuales hay algunos contenidos en los de la forma J . Sea N 0(
, entre los cuales hay algunos contenidos en los de la forma J . Sea N 0(  ) el subconjunto de índices j
) el subconjunto de índices j  N (
N (  ) para los cuales existe algún m de modo que
) para los cuales existe algún m de modo que 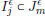 . Así tenemos:
. Así tenemos:
Читать дальше

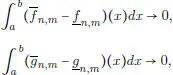
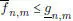 , si es necesario reemplazando
, si es necesario reemplazando 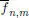 por ínf
por ínf 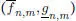 y
y 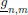 por sup
por sup 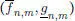 . Entonces,
. Entonces,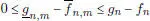
 . Tomando enseguida las sucesiones diagonales
. Tomando enseguida las sucesiones diagonales 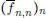 y
y 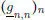 se tiene que ellas son aproximantes de f en el sentido de la definición de la integral de Riemann y
se tiene que ellas son aproximantes de f en el sentido de la definición de la integral de Riemann y 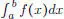 es igual al límite común de las integrales de tales funciones escalonadas. Pero además por construcción de las sucesiones de funciones escalonadas, los límites de sus integrales deben coincidir con los de la ecuación (1.34).
es igual al límite común de las integrales de tales funciones escalonadas. Pero además por construcción de las sucesiones de funciones escalonadas, los límites de sus integrales deben coincidir con los de la ecuación (1.34).
 > 0 existe una colección finita de intervalos
> 0 existe una colección finita de intervalos 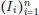 cuyo largo total (calculado como la suma de las longitudes respectivas) sea menor que e y su reunión cubre a N .
cuyo largo total (calculado como la suma de las longitudes respectivas) sea menor que e y su reunión cubre a N . y acotada. Ella es integrable en el sentido de Riemann sobre [ a , b ] si y sólo si su conjunto de discontinuidades D fes de extensión nula.
y acotada. Ella es integrable en el sentido de Riemann sobre [ a , b ] si y sólo si su conjunto de discontinuidades D fes de extensión nula.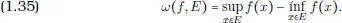
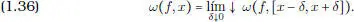
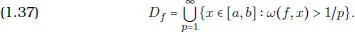
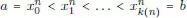 . Examinemos (1.24). Dado p > 1, E pqueda contenido en los intervalos de la partición π ( n ) en los cuales la oscilación
. Examinemos (1.24). Dado p > 1, E pqueda contenido en los intervalos de la partición π ( n ) en los cuales la oscilación  es mayor que 1/ p . Llamemos l n ( p ) la suma de las longitudes de dichos intervalos. Se tiene entonces
es mayor que 1/ p . Llamemos l n ( p ) la suma de las longitudes de dichos intervalos. Se tiene entonces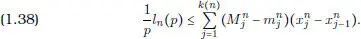
 que cubren E p y cuya suma de longitudes es menor que
que cubren E p y cuya suma de longitudes es menor que 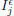 de extremidades
de extremidades 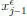 y
y 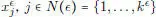 , entre los cuales hay algunos contenidos en los de la forma J . Sea N 0(
, entre los cuales hay algunos contenidos en los de la forma J . Sea N 0( 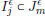 . Así tenemos:
. Así tenemos:










