Rolando Rebolledo B. - Teoría de la medida e integración

EDICIONES UNIVERSIDAD CATÓLICA DE CHILE

Vicerrectoría de Comunicaciones

Av. Libertador Bernardo O’Higgins 390, Santiago, Chile

editorialedicionesuc@uc.cl

www.ediciones.uc.cl

TEORÍA DE LA MEDIDA E INTEGRACIÓN

Volumen I

Rolando Rebolledo Berroeta

© Inscripción N° 270.153

Derechos reservados

Septiembre 2016

Reimpresión 2017

ISBN edición impresa 978-956-14-1964-3

ISBN edición digtial 978-956-14-2648-1

Diseño:

versión | producciones gráficas Ltda.

Diagramación digital: ebooks Patagonia

info@ebookspatagonia.com

www.ebookspatagonia.com

CIP - Pontificia Universidad Católica de Chile

Rebolledo, Rolando

Teoría de la medida e integración / Rolando Rebolledo Berroeta. –

Incluye bibliografía

1. Teoría de la medida.

2. Integrales

I. t.

2016 515.42 + dc 23 RCAA2

A Loreto y nuestro gran conglomerado familiar.

ÍNDICE GENERAL

Prefacio

Capitulo 1. Del arte de míedir

1. Asociando un número a un conjunto

2. Superficies en el plano

3. La integral de Riemann

4. La integral de funciones con valores complejos

5. Comentarios

6. Ejercicios propuestos

Capitulo 2. Estructuras Básicas

1. Complementos sobre la teoría de conjuntos

2. Pavimentos, semiálgebras, álgebras, tribus, clases monótonas

3. Ejemplos de Tribus

4. Funciones y Aplicaciones Medibles

5. Producto de espacios medibles

6. Medibilidad de las funciones numéricas

7. Historias y tiempos de parada

8. Comentarios

9. Ejercicios propuestos

Capítulo 3. Medidas positivas

1. Espacios de Medida

2. Conjuntos Despreciables

3. Extensión de medidas

4. Demostración del Teorema de Carathéodory

5. Comentarios

6. Ejercicios propuestos

Capítulo 4. Definición de la integral y propiedades elementales

1. La Integral de una Función Simple

2. Integral de funciones medibles positivas

3. Definición general de la integral

4. Integración de funciones complejas

5. La integral de Lebesgue

6. Familias Sumables

7. Comentarios

8. Ejercicios propuestos

Capítulo 5. Teoremas de Convergencia de las Integrales

1. Teoremas de Convergencia Monótona

2. El Teorema de la Convergencia Dominada de Lebesgue

3. Integrabilidad uniforme

4. Aplicaciones de los teoremas de convergencia

5. El Teorema de Daniell

6. Comentarios

7. Ejercicios propuestos

Capítulo 6. Integración en un espacio producto

1. Producto de medidas

2. El Teorema de Fubini

3. Comentarios

4. Ejercicios propuestos

Capítulo 7. Cambio de variables en la integral

1. Imagen de una medida por una aplicación medible

2. Aplicación: Convolución de medidas

3. Cambio de variables en la integral de Lebesgue en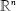

4. Comentarios

5. Ejercicios propuestos

Capítulo 8. Espacios de Banach y de Hilbert

1. Semi-norma sobre un espacio vectorial

2. Aplicaciones lineales continuas

3. Espacios normados de dimensión finita

4. Espacios de Banach

5. El espacio de Banach de las funciones continuas sobre un compacto

6. Acerca del teorema general de Stone-Weierstrass

7. Producto escalar

8. Proyecciones en un espacio de Hilbert

9. Dualidad en los espacios de Hilbert

10. Sistemas ortonormales en espacios pre-Hilbert

11. Bases ortonormales

12. Comentarios

13. Ejercicios propuestos

Capítulo 9. Los espacios L p

1. Algunas desigualdades de concavidad

2. Los espacios L p(1 ≤ p ≤ ∞)

3. Desigualdad de Hölder

4. Teorema de dualidad de Riesz para los espacios L p

5. Aplicación: Series de Fourier

6. Comentarios

7. Ejercicios propuestos

Capítulo 10. Medidas reales o complejas

1. Medidas reales. Descomposición de Jordan-Hahn

2. Medidas de Radon

3. Teorema de Radon-Nikodym y descomposición de Lebesgue

4. Aplicación: Condicionamiento en Teoría de Probabilidades

5. Propiedades de la esperanza condicional

6. Comentarios

7. Ejercicios propuestos

Capítulo 11. Apéndice 1: Más allá de la medida

1. Conjuntos analíticos

2. Capacidades y el Teorema de Choquet

3. Construcción de capacidades. Extensión de medidas

4. Aplicaciones

Capítulo 12. Apéndice 2: Facsímiles de interrogaciones resueltas

Índice alfabético

Bibliografía

PREFACIO

Esta obra está concebida como un libro de texto para estudiantes de la Licenciatura en Matemáticas o de la carrera de Ingeniería Matemática. El texto del primer volumen enseña las bases, métodos y resultados más importantes de la Teoría de la Medida e Integración, rama fundamental de la Matemática contemporánea que es prerrequisito para estudiar una variada gama de otras disciplinas como el Análisis Funcional, cursos avanzados sobre Ecuaciones Diferenciales, la Teoría de Sistemas Dinámicos, la Teoría de Probabilidades, la Estadística, Métodos de la Física Matemática, Análisis Estocástico, entre muchas otras. El segundo volumen, en preparación, se concentrará en las topologías débiles de medidas, el Análisis de Fourier, la versión funcional de la integral y elementos de la teoría no conmutativa, temas todos que corresponden más bien a cursos de postgrado.

La elección de los temas de este primer volumen ha seguido los diseños curriculares de los cursos de formación de matemáticos según estándares internacionales. Las primeras versiones de este texto remontan a la época en que enseñaba la Teoría de la Integración primero en Niza y luego en París, con un programa un poco más extenso. Luego, fue adaptado al programa del curso que se enseña en la Facultad de Matemáticas de la Universidad Católica y devino un apunte en Castellano, manuscrito y fotocopiado para los estudiantes hasta que la aparición de LA TEX permitió hacer una primera versión mecanografiada allá por la segunda mitad de la década de los 80. Desde entonces el texto, modificado sin cesar, ha circulado de manera supuestamente restringida al uso exclusivo de mis alumnos, si bien he sabido que algunas versiones han trascendido esa frontera y me ocurre recibir mensajes de estudiantes de otros lugares que piden acceder a los archivos de pruebas resueltas para ejercitar su aprendizaje.

Es muy importante en todo estudio científico considerar que no podemos conocer un objeto si no lo transformamos, y eso tiene una expresión muy clara en Matemáticas. No podemos aprender un tema nuevo si no intentamos probar los principales resultados nosotros mismos, y para ello los ejercicios son fundamentales. A través de ellos se puede entender mejor la historia de las ideas que llevaron al estado actual de una teoría; ellos constituyen para los matemáticos su laboratorio natural. En este volumen me he preocupado de proponer al final de cada capítulo listas de ejercicios que permitan al estudiante poner a prueba su comprensión de la teoría.