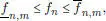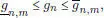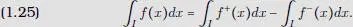
5. f  R ( I ) si y sólo si | f |
R ( I ) si y sólo si | f |  R ( I ) y se cumple:
R ( I ) y se cumple:

6. Si a < c < b , entonces f  R ([ a , b ]) si y sólo si f es a la vez integrable sobre [ a , c ] y [ c , b ]. En ese caso se tiene:
R ([ a , b ]) si y sólo si f es a la vez integrable sobre [ a , c ] y [ c , b ]. En ese caso se tiene:
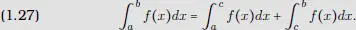
7. (Cambio de variables). Sea φ unafunción biyectiva del intervalo [ a , b ] sobre [ α , β ], de clase C 1 sobre ] a , b [. Para toda función f integrable en el sentido de Riemann sobre [ α , β ], la función t ↦ f ( φ ( t ))| φ′ ( t )| es integrable y se tiene la igualdad1
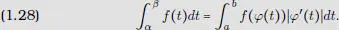
8. Sean f , g  R ([ a , b ]), tales que g mayore a f. Entonces [[ f , g ]] tiene superficie y
R ([ a , b ]), tales que g mayore a f. Entonces [[ f , g ]] tiene superficie y
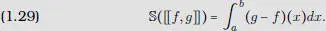
Demostración. Proponemos al lector que escriba completamente la demostración del teorema a título de ejercicio: a continuación le entregamos una rápida guía para hacerlo.
Se verifica fácilmente que las funciones escalonadas cumplen las distintas propiedades enunciadas en el teorema. Enseguida se trata de extender éstas a funciones arbitrarias, integrables en el sentido de Riemann. Esta extensión no presenta dificultades en el caso de las dos primeras propiedades. Para probar la tercera, observar en primer lugar que si α , α′ , β , β′ , son cuatro números reales, tales que α < α′ , β < β′ , entonces se cumplen las desigualdades siguientes:
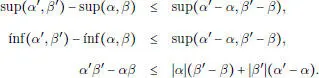
Hay que tener en cuenta además que si f  R ( I ) es mayorada en valor absoluto por una constante positiva M entonces se puede escoger las sucesiones aproximantes
R ( I ) es mayorada en valor absoluto por una constante positiva M entonces se puede escoger las sucesiones aproximantes 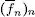 y
y 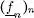 de modo que
de modo que
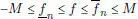
De este modo se puede entonces probar la tercera propiedad del enunciado. La cuarta es un caso particular de la tercera y de la linealidad de la integral; la quinta, resulta de la cuarta y de la igualdad:
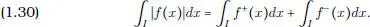
La sexta propiedad resulta de la observación siguiente: si [ α , β ] es un intervalo, 1 [α, β]( x ) es su función característica,(aquélla que vale 1 si x  [ α , β ] y 0 sino), entonces para toda función g sobre [ a , b ] se tiene:
[ α , β ] y 0 sino), entonces para toda función g sobre [ a , b ] se tiene:

De esta relación resulta claro que g = | f | es integrable si y sólo si | f |1 [a, c[y | f |1 [c, b]lo son. Pero, 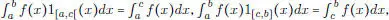 de modo que usando (1.31) con g = f se obtiene la descomposición del enunciado.
de modo que usando (1.31) con g = f se obtiene la descomposición del enunciado.
Un cálculo directo permite probar que la fórmula del cambio de variables es satisfecha por las funciones f escalonadas. Para extenderla a las funciones integrables en el sentido de Riemann, la clave es probar primero que si se tiene una función real f definida sobre [ a , b ] y si ( f n ) n, ( g n ) nson dos sucesiones de funciones integrables tales que
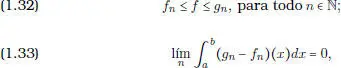
entonces f  R ([ a , b ]) y
R ([ a , b ]) y
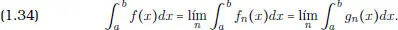
La demostración de esta propiedad se obtiene de la manera siguiente. Por la definición de la integral de Riemann, para todo n  existen sucesiones de funciones escalonadas
existen sucesiones de funciones escalonadas 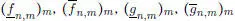 , tales que
, tales que
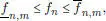
y
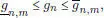
para todo m  y para las cuales
y para las cuales
Читать дальше

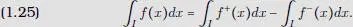
 R ( I ) si y sólo si | f |
R ( I ) si y sólo si | f | 
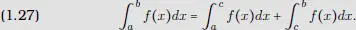
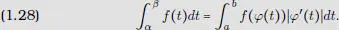
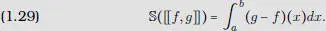
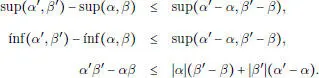
 R ( I ) es mayorada en valor absoluto por una constante positiva M entonces se puede escoger las sucesiones aproximantes
R ( I ) es mayorada en valor absoluto por una constante positiva M entonces se puede escoger las sucesiones aproximantes 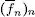 y
y 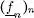 de modo que
de modo que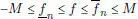
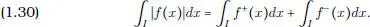

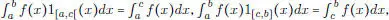 de modo que usando (1.31) con g = f se obtiene la descomposición del enunciado.
de modo que usando (1.31) con g = f se obtiene la descomposición del enunciado.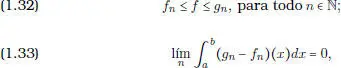
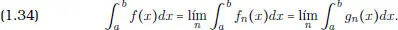
 existen sucesiones de funciones escalonadas
existen sucesiones de funciones escalonadas 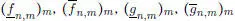 , tales que
, tales que