A demand-side management model can also include a model for tertiary control in microgrids or a model for charging electric vehicles. The latter is usually called vehicle-to-grid or V2G. In these cases, the optimization model requires to be executed in real-time by an aggregator as depicted in Figure 1.4.
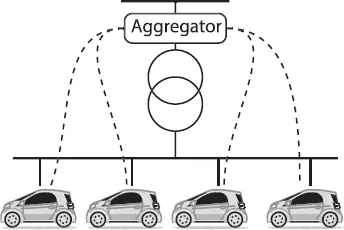
Figure 1.4 Vehicle-to-grid concept with an aggregator that centralizes control actions. Dashed lines represent a communication architecture with the aggregator.
An aggregator is a crucial component in modern smart distribution networks. This device receives information of the final users – in this case, the electric vehicles – and gives the control actions in order to obtain a smart operation. However, the intelligent part of this system is not in the hardware but in the optimization required to solve the problem efficiently and in real-time; therein lies the importance of understanding the optimization model.
A V2G strategy can be unidirectional or bidirectional. In unidirectional V2G, an aggregator controls the electric vehicles’ charge similarly as shifting loads. In bidirectional, the electric vehicle can inject power into the grid if required for improving the operation. In any case, the model can become stochastic since the state of charge of the vehicles can be unknown, and the aggregator does not control the arrival/departing time of the vehicles 1. The aggregator can also incorporate economic dispatch and OPF models to manage other distributed resources such as local batteries, solar panels, and wind turbines. Chapter 11examines these problems.
1.2.7 Energy storage management
Modern power systems can integrate renewable energy and energy storage devices through a virtual power plant (VPP), an entity that group and centralize the operation of distributed resources to be dispatched by the power system operator. A VPP can encompass an entire region with different renewable sources and energy storage devices. It can also group other microgrids along a distribution feeder.
There are at least two moments where optimization models are required: day-ahead dispatch and real-time operation. Day-ahead dispatch corresponds to the optimization model executed the day before the operation as an economic dispatch model (see Section 1.2.1). This model must include the availability of generation and consider a forecast of the primary resource (inflows, wind, and solar radiance). Moreover, it gives the value power that the VPP operator undertakes on the day of the operation. During the operation, the VPP requires satisfying operative constraints and correcting errors in forecasting the primary resource. Again, a real-time algorithm is necessary for energy storage management.
1.2.8 State estimation and grid identification
The problem of state estimation is classic in power systems. It is also a key component in Supervisory Control And Data Acquisition (SCADA) systems. The problem consists in determining the most probable state of the system from redundant measurements and knowledge of the topology and electrical relations of the grid. When the variables to be measured are active and reactive powers, a non-convex problem is obtained with the same degree of complexity as the load flow. Modern technologies such as the phasor measurement units (PMUs) allow to include direct measures of voltages and angles.
The problem can be also formulated in power distribution networks and microgrids, both AC and DC. Figure 1.5 shows, for example, a microgrid with a centralized control. Each active element of the network can have both voltage and current measurement. We can use these measurements in order to find the most likely state of the system based on the least squares model as shown below:
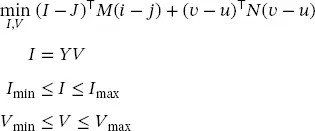 (1.6)
(1.6)
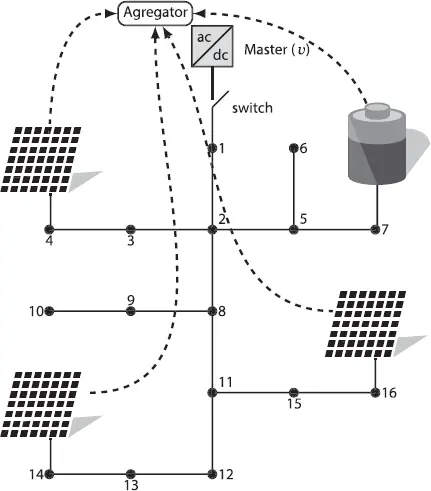
Figure 1.5 Example of a microgrid with a centralized control/measurement in the aggregator.
where J , U are measurements of current and voltage, respectively; I , V are the corresponding estimations and M , N are diagonal matrices that represent the weight of each measurement. The state estimation problem is closely related to the optimal power flow. In fact, some authors call this problem as the inverse power flow problem. The problem is studied in more detail in the second part of the book ( Chapter 12).
Another operation problem, closely linked to the state estimation, is the identification of the network. In this case, we have measurements of both voltages and currents at different operating points. Our goal is to estimate the value of the nodal admittance matrix from these measurements. In this case, the optimization model is the following:
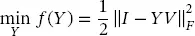 (1.7)
(1.7)
The decision variable is the nodal admittance matrix Y , and the objective function is the norm of error between measurements and estimations 2.
The model can include information about the structure of the matrix Y . For example, we already know that the matrix is symmetric and, some of its entries are zero. In that case, the optimization model is the following:
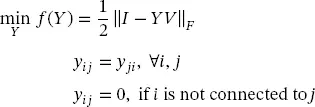 (1.8)
(1.8)
Both AC and DC grids may handle this type of estimation. In this case, we only presented the DC case because it is easier to develop. The entire model must be implemented in an aggregator structure, as depicted in Figure 1.5.
1.3 Binary problems in power systems operation
Some of the problems previously described are binary. These problems appear in electrical systems, both in the planning and the operation stages. In the planning stage, the problems of transmission expansion planning and distribution planning are typical. Heuristic techniques usually solve these problems together with mixed-integer programming approximations [3]. Although mixed-integer problems are non-convex, they can be solved efficiently using methodologies such as the branch-and-bound algorithm. We present a brief introduction of this method in Chapter 4. Besides, several modules can be called from Python to solve these types of problems. We used Gurobi and Mosek for this task, although there are plenty of options available. Binary operation problems include unit commitment and phase balancing in power distribution networks.
As aforementioned, the unit commitment problem consists in determining the order of starting and stopping of the thermal units, taking into account the costs of turning-ON and turning-OFF, as well as the starting ramps. The optimization model is similar to the economic dispatch, but in this case, there are binary variables sk related to the state ON or OFF of each thermal unit. The most simplified model is presented below:
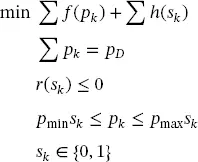 (1.9)
(1.9)
Читать дальше


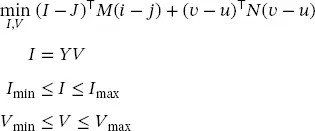 (1.6)
(1.6)
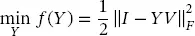 (1.7)
(1.7)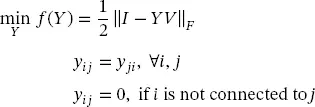 (1.8)
(1.8)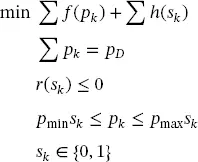 (1.9)
(1.9)










