141 128
142 129
143 130
144 131
145 132
146 133
147 134
148 135
149 136
150 137
151 138
152 139
153 140
154 141
155 142
156 143
157 144
158 145
159 146
160 147
161 148
162 149
163 150
164 151
165 152
166 153
167 154
168 155
169 156
170 157
171 158
172 159
173 160
174 161
175 162
176 163
177 164
178 165
179 166
180 167
181 168
182 169
183 170
184 171
185 172
186 173
187 174
188 175
189 176
190 177
191 178
192 179
193 180
194 181
195 182
196 183
197 184
198 185
199 186
200 187
201 188
202 189
203 190
204 191
205 192
206 193
207 194
208 195
209 196
210 197
211 198
212 199
213 200
214 201
215 202
216 203
217 204
218 205
219 206
220 207
221 208
222 209
223 210
224 211
225 212
226 213
227 214
228 215
229 216
230 217
231 218
232 219
233 220
234 221
235 222
236 223
237 224
238 225
239 226
240 227
241 228
242 229
243 230
244 231
245 232
246 233
247 234
248 235
249 236
250 237
251 238
252 239
253 240
254 241
255 242
256 243
257 244
258 245
259 246
260 247
261 248
262 249
263 250
264 251
265 252
266 253
267 254
268 255
269 256
270 257
271 258
272 259
273 260
274 261
275 262
276 263
277 264
278 265
279 266
280 270
281 271
282 272
283 273
284 274
285 275
286 276
287 277
288 278
289 279
290 280
291 281
292 282
Throughout the writing of this book, I have received a great deal of support and assistance from many people. I would first like to thank my friends Lucas Paul Perez at Welltec, Adrian Correa at Universidad Javeriana in Bogotá-Colombia, Ricardo Andres Bolaños at XM (the transmission system operator in Colombia), Raymundo Torres at Sintef-Norway, and Juan Carlos Bedoya at the Pacific Northwest National Laboratory (USA), who, in 2020 (during the COVID-19 pandemic), agreed to discuss some practical aspects associated to power system operation problems. The discussions during these video conferences were invaluable to improve the content of the book. I am also very grateful to my students, who are the primary motivation for writing this book. Special thanks to my former Ph.D. students, Danilo Montoya and Walter Julian Gil. Finally, I want to thank the Department of Electric Power Engineering at the Universidad Tecnológica de Pereira in Colombia and the Von Humbolt Foundation in Germany for the financial support required to continue my research about the operation and control of power systems.
Alejandro Garcés
Electrification is the most outstanding engineering achievement in the 20th century, a well-deserved award if we consider the high complexity of generation, transmission, and distribution systems. An electric power system includes hundreds or even thousands of generation units, transformers, and transmission lines, located throughout an entire country and operated continuously 24 hours per day. Running such a complex system is a great challenge that requires using advanced mathematical techniques.
All industrial systems seek to increase their competitiveness by improving their efficiency. Electric power systems are not the exception. We can improve efficiency by introducing new technologies but also by implementing mathematical optimization models into daily operation. In every mathematical programming model, we require to perform four critical stages depicted in Figure . The first stage is an informed review of reality, identifying opportunities for improvement. This stage may include conversations with experts in order to establish the available data and the variables that are subject to be optimized. The second stage is the formulation of an optimization model as given below:
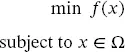 (0.1)
(0.1)
Where x is the vector of decision variables, f is the objective function and, Ω is the set of feasible solutions. Going from stage one (reality) to stage two (model) is more of an art than a science. One problem may have different models and different degrees of complexity. Practice and experience are required to master this stage, as some models are easier to solve than others. Subsequently, the third stage consists of the implementation of the mathematical model into a software. After that, the fourth stage is the analysis of results in the context of the real problem.
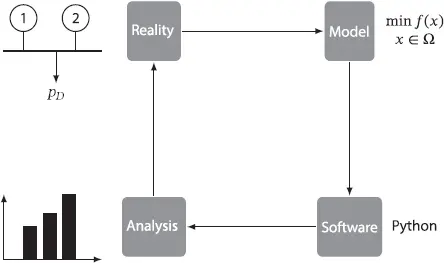
Figure 0.1Stages of solving an optimization problem.
This book will focus on stages two and three, associated with power system operations models. In particular, we are interested in models with a geometric characteristic called convexity , that present several advantages, namely:
We can guarantee the global optimum and unique solution under well-defined conditions. This aspect is interesting from both theoretical and practical points of view. In general, a global optimum advisable in real operation problems.
There are efficient algorithms for solving convex problems. In addition, we can guarantee convergence of these algorithms. This is a critical aspect for operation problems where the algorithm requires to be solved in real-time.
There are commercial and open-source packages for solving convex optimization models. In particular, we are going to use CvxPy, a free Python-embedded modeling language for convex problems.
Many power system operations problems are already convex; for example, the economic and environmental dispatches, the hydrothermal coordination, and the load estimation problem. Besides, it is possible to find efficient convex approximations to non-convex problems such as the optimal power flow.
In summary, convex problems have both theoretical and practical advantages for power systems operation. This book studies both aspects. The book is oriented to bachelor and graduated students of power systems engineering. Concepts related to power systems analysis such as per-unit representation, the nodal admittance matrix, and the power flow problem are taken for granted. A previous course of linear programming is desirable but not mandatory. We do not pretend to encompass all the theory behind convex optimization; instead, we try to present particular aspects of convex optimization which are useful in power systems operation. The book is divided into two parts: In the first part, the main concepts of convex optimization are presented, including a distinct chapter about conic optimization. After that, selected applications for power systems operation are presented. Most of the solvers for convex optimization allow mixed-integer convex problems. Therefore, we include models that can be solved in this framework too. The student is recommended to do numerical experiments in order to acquire practical intuition of the problems.
Читать дальше

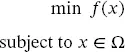 (0.1)
(0.1)











