1.2.3 Effect of the grid constraints
Both the economic dispatch of thermal units and the hydrothermal dispatch are relatively simple problems. However, the transmission grid introduces additional constraints. Let us consider, for example, a power system with three operation areas, as shown in Figure 1.3.
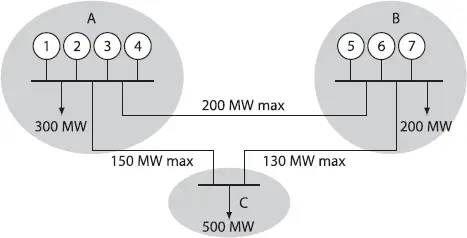
Figure 1.3 Economic dispatch by areas considering network constraints with the transport model.
Each line has a maximum power flow capacity that introduces additional constraints in the model (both economic dispatch and hydrothermal dispatch). This constraint limits the flow among areas and modifies the results. These aspects are studied in Chapter 7from a classic perspective and later, in Chapter 10, under a modern view based on conic optimization.
The power flow is one of the most important tools for the analysis of power systems. It allows to determine the state of the power system, knowing the magnitude of voltage and active power in all generating nodes and, active/reactive power demanded in the loads. This results in a non-linear system of equations in complex variables, as presented below:
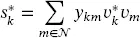 (1.3)
(1.3)
where sk = pk + qk represents the active and reactive power in node k ;  represents the set of nodes of the grid; ykm is the entry km of the Y busmatrix; vk and vk are the voltages at nodes k and m , respectively, both represented as complex variables; and sk* and vk* are the complex conjugate of the respective variables. This representation on the complex number can be splitted into real and imaginary parts. However, as presented in Chapter 10, a complex representation is suitable both for modeling and implementation purposes.
represents the set of nodes of the grid; ykm is the entry km of the Y busmatrix; vk and vk are the voltages at nodes k and m , respectively, both represented as complex variables; and sk* and vk* are the complex conjugate of the respective variables. This representation on the complex number can be splitted into real and imaginary parts. However, as presented in Chapter 10, a complex representation is suitable both for modeling and implementation purposes.
These constraints can be introduced into the economic dispatch, as well as in an optimization model that minimizes total power loss ( p loss). In both cases, we named the problem as OPF. The basic model has the following structure:
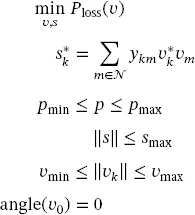 (1.4)
(1.4)
This problem is highly complex due to the non-linear and non-convex nature of the power flow equations. Therefore, it is required to review different approximations that simplify the model. Chapter 10presents three of these approximations. These are linearization, second-order cone approximation, and semidefinite programming approximation.
Linearization is, perhaps, the most straightforward way to solve the problem. Although the concept of linearization is well-known in real numbers, in this case, we do a linearization on the complex domain. This linearization uses Wirtinger’s calculus since ( Equation 1.3) is non-holomorphic (i.e., it does not have a derivative in the complex numbers). Chapter 10and Appendix B study this aspect in detail.
We also solve the optimal power flow using second-order cone and semidefinite programming. These approximations demand a basic understanding of conic optimization. Therefore, we present a general background of conic optimization in Chapter 5, and its application to the optimal power flow problem in Chapter 10, including a complete discussion about their advantages and disadvantages.
We also solve the optimal power flow using second-order cone and semidefinite programming. These approximations demand a basic understanding of conic optimization. Therefore, we present a general background of conic optimization in Chapter 5, and its application to the optimal power flow problem in Chapter 10, including a complete discussion about their advantages and disadvantages.
An optimal power flow may optimize both power systems and power distribution grids. However, the latter case presents some particularities that deserve an independent study. Moreover, both solar and wind energy require power electronic converters connected at power distribution level. These converters are capable of controlling reactive power, and therefore, it is possible to formulate an OPF wherein the decision variables are the power factor of each converter. The problem can be deterministic for real-time operation or stochastic for the day ahead planning. In both cases, the model has, at least, the same complexity as the basic OPF.
The concept of hosting capacity refers to the amount of solar photovoltaic generation (or wind) that can be hosted on a power distribution network, at a given time, without adversely impacting safety, power quality, reliability, or other operational features [1]. This analysis can use different performance criteria, including transient and stationary state analysis. The latter alludes to the maximum amount of generated power possible to host without creating over-voltage problems and maintaining operational limits on the distribution lines.
A hosting capacity analysis requires considering the stochastic nature of solar radiation and power demand [2]. Furthermore, it needs to consider the non-linear characteristics related to the power flow equations. Therefore, it is a problem as complex as the optimal power flow ( Chapter 11investigates this problem).
1.2.6 Demand-side management
Demand-side management constitutes a paradigm shift in the context of smart grids, where loads are active components subject to optimization. The role of demand-side management is crucial to decrease CO 2emissions, reduce the bottleneck in the transmission system, diminish operational cost, and improve efficiency. In order to attain these objectives, it is required to apply mechanisms of electrical load management with static and dynamic techniques. Static techniques involve administrative measures as policies and activities to incentive the end-users to change their energy demand pattern; dynamic techniques include actions to reduce the electricity consumption, such as peak-clipping, valley filling, and load shifting, among others. Information and communication technologies (ICT), as well as the concept of the Internet of the Things (IoT), allow to control the loads and integrate this control in a centralized optimization model.
In general, controllable loads are introduced in a model very similar to the economic dispatch. Its basic structure is presented below:
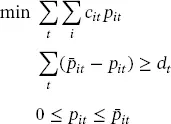 (1.5)
(1.5)
where p¯it is the power required by the load i at time t ; pit is the amount of power that is reduced due to the demand-side management model; cit is the cost of disconnecting one unit of power; and dt is the minimum demand. This is only the basic optimization model, which can be modified, in order to include more type of loads and other aspects of the operation of the system.
Some loads can be moved in time, for example, the washing machine in a residential user. These loads, known as shifting loads, can be optimized by defining the load’s optimal starting time. This optimization model is binary but tractable as presented in Chapter 13.
Читать дальше


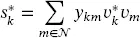 (1.3)
(1.3) represents the set of nodes of the grid; ykm is the entry km of the Y busmatrix; vk and vk are the voltages at nodes k and m , respectively, both represented as complex variables; and sk* and vk* are the complex conjugate of the respective variables. This representation on the complex number can be splitted into real and imaginary parts. However, as presented in Chapter 10, a complex representation is suitable both for modeling and implementation purposes.
represents the set of nodes of the grid; ykm is the entry km of the Y busmatrix; vk and vk are the voltages at nodes k and m , respectively, both represented as complex variables; and sk* and vk* are the complex conjugate of the respective variables. This representation on the complex number can be splitted into real and imaginary parts. However, as presented in Chapter 10, a complex representation is suitable both for modeling and implementation purposes.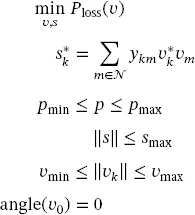 (1.4)
(1.4)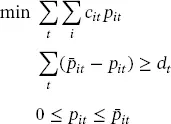 (1.5)
(1.5)










