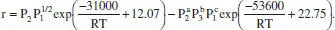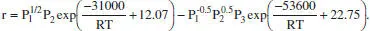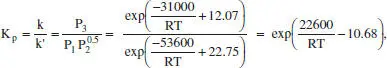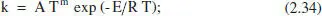Àngel Berna Prats - Introducció a l'enginyeria dels reactors químics

on E i E’ són les energies d’activació dels camins directe i invers, i A i A’ els factors preexponencials corresponents.

Exemple 2.3

La cinètica de la reacció SO 2+ 0.5 O 2↔ SO 3(A 1+ 0.5 A 2↔ A 3) amb un catalitzador de vanadi ve donada per l’expressió ( r en mol/s g de cat.)

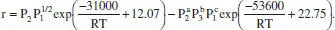
Les energies d’activació vénen en cal/mol i P jen atm. Calculeu els valors dels ordres a , b i c que fan que aquesta equació cinètica siga coherent. Així mateix, trobeu una expressió per a la constant d’equilibri en funció de la temperatura.

Solució:

a) Determinació dels ordres de la reacció inversa. Atès que es coneixen els ordres de la reacció directa i els coeficients estequiomètrics, podem determinar els ordres buscats aplicant la relació que resulta de tenir en compte la consistència termodinàmica del model cinètic: γ j- β j= v j. Cal recordar que aquesta equació té una forma més general: γ j- β j= n v j.

Aplicant aquesta equació amb n = 1 al nostre problema, calcularem γ j, i aprofitarem el càlcul per analitzar el comportament de cada espècie, a fi de detectar comportaments autocatalítics.

Reacció: ;SO 2+ 0.5 O 2↔ SO 3. Forma seneralitzada: - A 1- 0.5 A 2+A 3= 0.

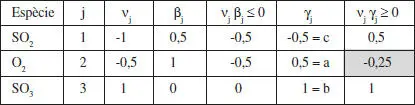
El model cinètic queda:

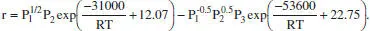
S’ha detectat un comportament autocatalític per a l’oxigen en la reacció inversa. Aquesta espècie per a aquesta reacció és un producte; no obstant això, té un efecte positiu sobre la velocitat de reacció.

b Expressió K = f(T). Si apliquem el model cinètic a la situació d’equilibri: r = 0, i ordenem 1'expressió resultant, es té

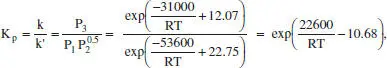
d’on, d’acord amb l’equació de Van’t Hoff,ΔH = -22600 cal/mol, es tracta, doncs, d’una reacció exotèrmica.

La influència de la temperatura sobre la velocitat de reacció apareix de forma explícita en les constants cinètiques a través d’equacions del tipus d’Arrhenius [k = A exp(-E/RT)]. Convé recordar que la deducció d’aquesta equació no és excessivament rigorosa; no obstant això, la seua utilitat en gran nombre de casos (molts d’ells en sistemes que no tenen res a veure amb la cinètica qufmica) fa que s’utilitze de forma indiscriminada. En la figura 2.5 es reprodueix un comportament normal (típic d’Arrhenius, m = 0). Els autors recomanen la lectura de la discussió que sobre el model d’Arrhenius apareix en el llibre de Nauman (1987), on es mostra el cas d’una reacció en què la linealitat es manté sobre un interval de més de 2000 graus. No obstant això, la figura 2.6 mostra una reacció amb desviacions clares d’aquesta linealitat; en alguns exemples de l’obra de Nauman apareixen reaccions en les quals es pot veure un canvi en el signe de l’energia d’activació. Les dades de la figura 2.6 corresponen a la reacció Al + CO 2→ AlO + CO, i han sigut obtingudes del treball de Fontjin i Feider (1977).

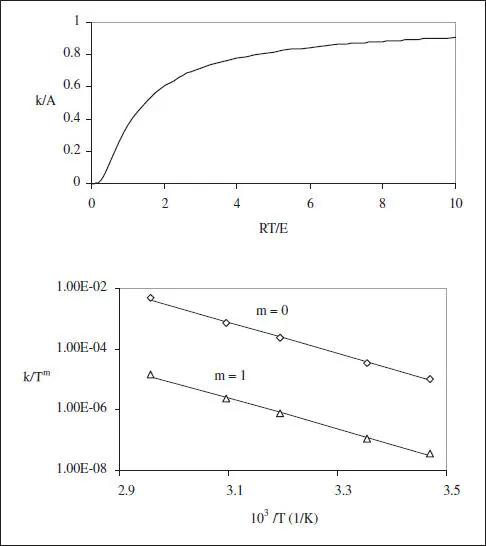
Figura 2.5. Exemple de reacció que segueix el model d’Arrhenius.

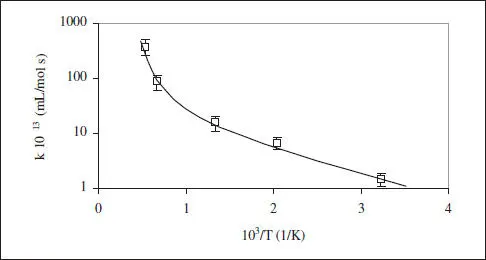
Figura 2.6. Exemple de reacció que es desvia del model d’Arrhenius.

En alguns casos es prefereix utilitzar una versió més rigorosa de l’equació d’Arrhenius:

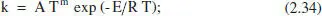
el paràmetre m sol estar comprès entre 0 i 1. En la figura 2.5 es mostren les representations d’Arrhenius per a dos valors de m: m = 0 (cas normal), i m = 1, per a la reacció N 2O 5→ N 2O 4+ 0.5 O 2. En tots els casos la linealitat és perfecta. Aquestes dades corresponen a un exemple recollit en el llibre de Hill (1977).

Exemple 2.4

Es disposa de la informació que es mostra en la taula E2.4 sobre la constant cinètica de la reacció N 2O 5→ N 2O 4+ 0.5 O 2Calculeu les constants de l’equaciód’Arrhenius per a aquest cas.

TAULA E2.4

Constant cinètica de la reacció N2O5 → N2O4 + 0.5 O2

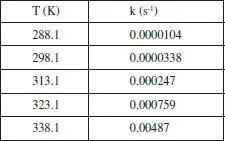
Repetiu el càlcul, suposant que la relació de k amb la temperatura ve donada per l’equació (2.34), amb m=1.

Solució :

Linealitzant el model d’Arrhenius, es té k = A exp(-E/RT), ln k = ln A -E/RT.

Efectivament, en representar ln k enfront de la inversa de la temperatura absoluta s’obté una línia recta. Els paràmetres de l’ajust lineal són: Ordenada en l’origen = 30.02, Pendent = -1.2 10 4, i els paràmetres del model d’Arrhenius: A = 1.1 10 13s -1i E = 23822 cal/mol, el paràmetre r 2= 0.998. La suma de les desviacions al quadrat val 2.8 10 -7.

Aplicació del model en la forma k = A T mexp(-E/RT) amb m=1. Es pot reproduir l’anàlisi anterior amb el consegüent canvi: Model: k = A T exp(-E/RT), Model linealitzat: ln (k/T) = ln A - E/RT.

De nou, en representar ln (k/T) enfront de la inversa de la temperatura absoluta s’obté una línia recta. Els paràmetres de l’ajust lineal són: Ordenada en l’origen = 23.28, Pendent = -1.2 10 4, i els paràmetres del model: A = 1.3 10 10s -1K -1i E = 23202 cal/mol, i el paràmetre r 2= 0.998. Els resultats d’aquesta anàlisi s’han mostrat en la figura 2.5.

L’ajust lineal per mínims quadrats és un procediment senzill i automatitzat, però per a ser aplicat necessita que es complisquen alguns requisits. Un d’aquests requisits és que els errors experimentals (de la variable dependent, ja que la independent se’n considera exempta) estan distribuïts normalment. L’única transformació que no altera la distribució dels errors és l’addició o la multiplicació per una constant. La transformació logarítmica no seria, per tant, correcta. La variable independent pot transformar-se a causa de l’absència d’error que se li suposa.

Per això, pareix més correcte realitzar l’ajust per procediments no lineals. En aquest cas s’ha utilitzat l’eina Solver del full de càlcul EXCEL. El resultat obtingut utilitzant l’equació d’Arrhenius ha sigut A = 7.2 10 12s -1i E = 23474 cal/mol. La suma dels errors al quadrat val 4.2 10 -8. Això suposa una millora respecte a l’ajust lineal. En la figura E2.4 es pot veure la comparació d’ambdós procediments d’ajust.