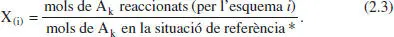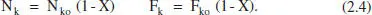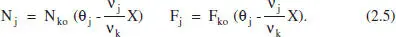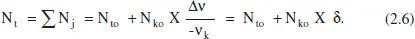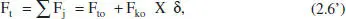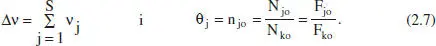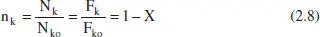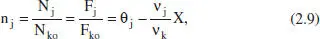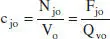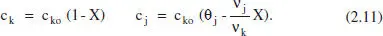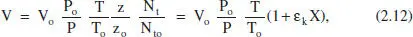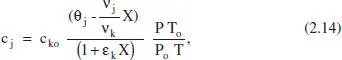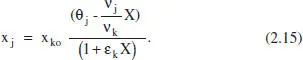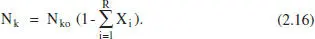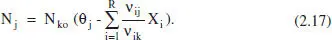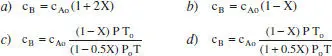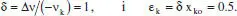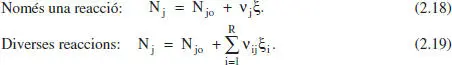Àngel Berna Prats - Introducció a l'enginyeria dels reactors químics

Així, per a sistemes en què hi ha una sola reacció (o si n’hi ha diverses, per a una d’elles),

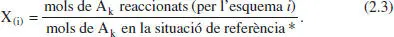
El parèntesi de Fequació (2.3) indica que si es té una única reacció no cal indicar-ho amb el subíndex. En cas contrari, quan hi ha diverses reaccions, cal indicar amb el subíndex la reacció de què es tracta. Alguns autors posen un subíndex, fent referènda al component clau, encara que no tinguen més que una reacció.

La situació de referènda * és:

- La inicial (a t = 0) per a un sistema discontinu.

- La de l’entrada del reactor per a un sistema continu.

Aquestes situacions de referènda s’il·lustren en la figura 2.1.

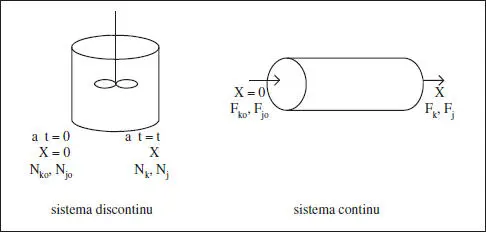
Figura 2.1. Situacions de referènda per a un sistema discontinu i un sistema continu.

Això porta a les següents equacions per als canvis de composició: - Si tenim una sola reacció, les variables extensives quedaran: Component clau:

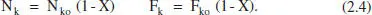
Per a qualsevol component:

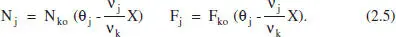
I el nombre total de mols del sistema:

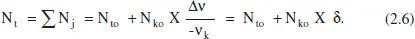
De la mateixa manera, el cabal molar total serà:

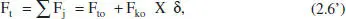
on

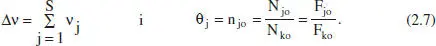
- I les variables intensives:

la rao molar n j :

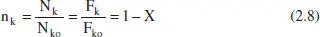
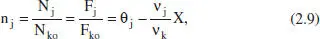
i la concentracio molar c j:

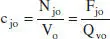
Aquesta variable mostra, tal com s’acaba de recordar, la relació entre el nombre de mols de l’espècie j i el volum del sistema. En avangar la reacció, poden canviar tots dos membres d’aquesta relació. Per això, es distingirà entre sistemes de densitat constant i aquells que són de densitat variable. En els sistemes de densitat constant, tenint en compte (2.4), (2.5) i (2.10), i que V o= V (o Q vo= Q v):

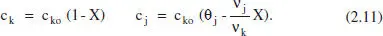
En els sistemes de densitat variable s’ha de descriure, a més a més, la variació de V (o de Q v) amb la conversió. Així, per exemple en un sistema discontinu gasós, el volum de reacció pot canviar, si l’entorn del sistema li ho permet, perquè canvia la pressió, la temperatura i/o el nombre de mols per la reacció química.

a temps t = 0 P oV o= z oN toR T oen un altre temps t P V = z N tR T

Dividint ambdues expressions i ordenant:

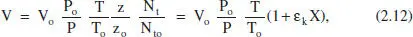
on s’ha considerat que el factor de compressibilitat ( z ) no canvia pràcticament. A més a més, l’ultim parèntesi representa la variació relativa del nombre total de mols a causa de la reacció, per al qual s’ha tingut en compte l’equació (2.6), i que anomenem ε kal producte x koδ. Per a entendre el significat de ε k, pot considerarse la seua definició alternativa, el canvi fraccional del volum de la mescla reactiva en completar-se la reacció a causa de la variació en el nombre de mols:

L’equació resultant per a c jen aquest cas és

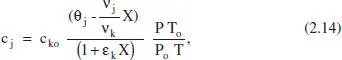
i per a la fracció molar x j,

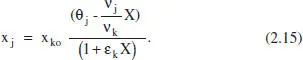
Si tenim diverses reaccions, les variables extensives quedaran: Component clau:

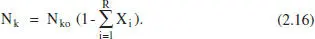
Per a qualsevol component:

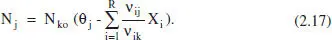
La traducció o extensió d’aquestes equacions a altres variables es pot efectuar seguint la metodologia exposada més amunt.

Exemple 2.2

Quina de les següents expressions correspon a la composició de B en un procés en què es desenvolupa la reacció en fase gas, elemental A + B → 2 C + D, en condicions no isotermes? L’aliment és equimolar en A i B.

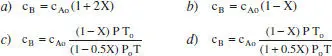
Solució:

Es tracta d’una reacció en fase gas: A + B → 2 C + D x Ao= x Bo= 0.5.

Com que Δv ≠ 0, el sistema pot ser de densitat variable. En aquest cas, Δv = -1-1+2+1 = 1, per la qual cosa, tenint en compte que s’ha triat A com a component clau,

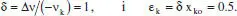
Per això, la solució serà la d. Si el sistema fóra un RDTA de V constant, el sistema seria de densitat també constant, amb la qual cosa la solució correcta seria la b .

2.2.3.2 Grau d’avang

La definició d’aquesta variable extensiva pot deduir-se de les següents expressions:

Només una reacció:

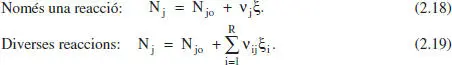
Cal adonar-se de les diferències entre el grau d’avanç (magnitud extensiva) i el de conversió (magnitud intensiva).