
on S és el nombre d’espècies del sistema, A jrepresenta l’espècie j i v jés el seu coeficient estequiomètric. Si hi ha diverses reaccions la seua representació serà
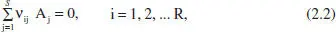
on R és el nombre de reaccions i v ijés el coeficient estequiomètric de Fespècie A jen l’esquema de reacció i.
Interessa treballar amb el menor nombre possible d’equacions, i per tant amb el menor nombre de reaccions. Hi ha procediments per a, coneguts els esquemes de reacció, determinar si hi ha entre ells alguna combinació lineal, per a eliminar-la i d’aquesta manera reduir la dimensió del problema. Així mateix, en la bibliografia hi ha altres procediments per a trobar un conjunt d’esquemes de reacció linealment independents, capagos d’explicar els canvis estequiomètrics que tenen lloc en el sistema. Aquesta opció és interessant en el cas que no es coneguen les reaccions que tenen lloc.
Exemple 2.1
El sistema format per les espècies N 2, O 2, NO i NO 2, s’ha representat per dues reaccions:
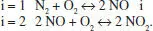
Podria haver-se representat només per una? Quants esquemes es necessitarien per a representar aquest sistema, considerant que hi ha, a més a més, dos òxids més: N 2O i N 2O 4?
Solució:
Vegem, en primer lloc, el nombre d’esquemes de reacció necessaris per a representar aquest sistema. Per a això comencem fent un recompte:
Espècies: N 2, O 2, NO i NO 2; és a dir, S = 4.
Elements: N, O; tenim, doncs, 2 elements.
Matriu elements-espècies: Els elements d’aquesta matriu assenyalen el nombre d’elements d’un determinat tipus que hi ha en una espècie determinada.
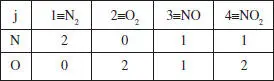
Es pot veure fàcilment que el rang d’aquesta matriu (l’ordre del determinant més gran no nul) és 2. És a dir, R ε= 2. Amb això, aplicant la regla de Gibbs, calculem R’ , el nombre de reaccions independents necessàries per explicar el sistema. Regla de Gibbs: R’ = S - R ε= 2.
Per tant es necessiten dos esquemes. L’enunciat proposa dos esquemes també, que contenen les 4 espècies. Per a saber si són vàlids, cal fixar-se si són independents. Veiem que ho són, ja que cada esquema té almenys una espècie que no està en l’altre, per tant no es pot obtenir una relació a partir de l’altra. Es pot veure que si sumem totes dues reaccions desapareix l’espècie NO, per la qual cosa aquest esquema de reacció suma no pot explicar els canvis de composició en el sistema.
En aquest cas ha sigut fàcil comprovar la independència de les reaccions, a causa del seu reduït nombre. Per això, apliquem un procediment que es pot automatitzar i estendre a casos més complicats. En aquest procediment escrivim la matriu de coeficients, en la qual, fent operacions permeses, cal aconseguir que la «diagonal principal» estiga formada per «1» (serveix qualsevol número distint de 0), i la part situada davall d’aquesta «diagonal principal» per 0. Si s’aconsegueix açò, els esquemes de reacció són independents; en cas contrari, apareixerà alguna fila formada únicament per 0. Açò indica que aquest esquema de reacció és dependent d’altres esquemes del sistema, per la qual cosa ha de ser eliminat.
En el nostre cas la matriu de coeficients és
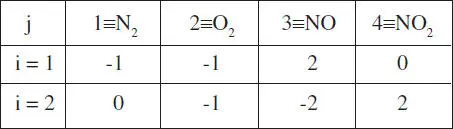
Es pot veure que, sense necessitat de fer cap càlcul, es té la situació buscada. Per això, els esquemes són independents.
Sobre el problema de la inclusió de dues espècies més (N 2O i N 2O 4), podem veure que el nombre d’espècies serà ara S = 6. Aquestes dues espècies no afigen cap element nou (estan formades ambdues per N i O. Per això, R ε= 2, i R’ = 4). Es necessitaran, per tant, 4 esquemes de reacció.
Una altra possibilitat, en relació amb aquest problema, és que coneguem les espècies implicades (N 2, O 2, NO i NO 2) i volem trobar uns esquemes de reacció que expliquen els canvis de composició del sistema. És a dir, suposem que l’enunciat no proposa cap esquema de reacció. Aleshores podem aplicar el mètode de Smith i Missen (1979, 1998). En aquest procediment, el punt de partida és la matriu elementsespècies descrita més amunt. Fent operacions elementals i raonables cal fer aparèixer la matriu identitat. La resta de la matriu ens donarà els coeficients estequiomètrics buscats. El problema plantejat és molt senzill, simplement cal dividir totes dues files per 2, i s’obté:
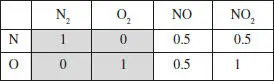
Les dues columnes que encapçalen la matriu identitat (marcada en gris) formen la base del sistema (N 2i O 2). Les dues columnes que no pertanyen a la base ens donen els coeficients estequiomètrics de les formacions d’aquests components a partir dels de la base:
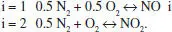
La solució no és única, per això aquestes reaccions no són les proposades abans (una si, l’altra no).
2.2.2 Mesura de la composició
La presència de reaccions en un sistema és percebuda pels canvis de composició que hi tenen lloc. Per això, en la taula 2.1 es recorden molt breument les formes més comunes de representar la composició.
TAULA 2.1
Variables de composició
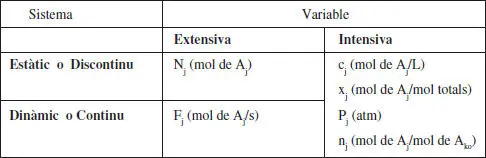
A kés el component clau definit en l’apartat 2.2.3.1.
Les relacions entre aquestes variables són senzilles d’establir, per exemple:

2.2.3
Mesures de l’avanç de la reacció
Aquestes variables indiquen els canvis de composició que tenen lloc en el sistema amb un sol valor per reacció. A continuació, es recorden algunes d’aquestes variables:
2.2.3.1 Grau de conversió
Representa la fracció reaccionada d’un component clau o de referència (A k). Encara que l’elecció d’aquest component és bastant arbitrària, sol tractar-se d’un reactiu. En el cas que hi haja una sola reacció, es recomana l’elecció del reactiu limitador; quan coexistisquen diverses reaccions, sol triar-se un reactiu comú. Si no hi ha cap reactiu comú, pot utilitzar-se un component clau distint per a cada reacció, encara que en aquest cas es recomana utilitzar una altra mesura de l’avanç de la reacció. Si hi ha més d’un reactiu comú, les regles per a l’elecció del component clau es compliquen, per la qual cosa el més senzill és triar-ne un qualsevol, ja que, al cap i a la fi, es tracta d’un component a què referir els càlculs.
Читать дальше


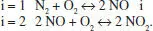



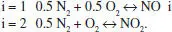

 2.2.3 Mesures de l’avanç de la reacció
2.2.3 Mesures de l’avanç de la reacció











