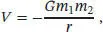
wobei G die (universelle) Gravitationskonstante ist. Für ein Objekt mit der Masse m an der Erdoberfläche ist das Gravitationspotenzial durch
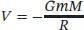
gegeben, wobei wir hier mit M die Masse der Erde und mit R den Radius unseres Planeten bezeichnen. Anhand dieses Ausdrucks können wir erkennen, dass das Potenzial an der Erdoberfläche gleich groß ist wie im imaginären Fall, wenn die gesamte Masse der Erde an einem Punkt im Abstand ihres Radius konzentriert wäre.
Während sich eine Masse von der Erdoberfläche entfernt, nimmt ihre potenzielle Energie stetig zu, d. h. sie wird weniger negativ; bei sehr großen Distanzen geht sie schließlich gegen null. Diese Änderung der potenziellen Energie muss vollständig in kinetische Energie umgewandelt werden, damit eine Masse die Gravitation überwinden kann. Eine Masse m, die sich mit der Geschwindigkeit v bewegt, besitzt die kinetische Energie 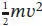 ; diese Geschwindigkeit entspricht der Fluchtgeschwindigkeit v e, wenn
; diese Geschwindigkeit entspricht der Fluchtgeschwindigkeit v e, wenn
(G1.3) 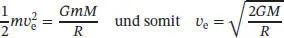
gilt. Der Term unter der Quadratwurzel hängt folgendermaßen mit der Beschleunigung des freien Falls, g, zusammen: Eine Masse m an der Erdoberfläche erfährt aufgrund der Gravitation eine Kraft, die GMm/R 2entspricht. (Beachten Sie, dass diese Kraft proportional zu R −2ist.) Diese Kraft beschleunigt die Masse in Richtung Erdoberfläche, und wir schreiben dafür (wie gewohnt) F = mg . Wenn wir diese beiden Ausdrücke für die Kraft gleichsetzen, erhalten wir
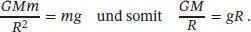
Wenn wir den Ausdruck für GM/R in die Beziehung für v eaus Gl. (G1.3)einsetzen, erhalten wir
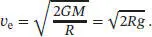
Wir sehen, dass die Fluchtgeschwindigkeit v esowohl eine Funktion des Erdradius R als auch der Beschleunigung des freien Falls g ist.
Der Radius der Erde ist R = 6,37 × 10 6m und g = 9,81 m s −2, daher ist die Fluchtgeschwindigkeit v e= 1,12 × 10 4m s −1. Zum Vergleich: die mittlere Geschwindigkeit von He bei 298 K ist 1300 m s −1, und für N 2beträgt sie 475 m s −1. Im Falle von Helium können nur solche Atome die Atmosphäre verlassen, die sich mit dem Achtfachen der mittleren Geschwindigkeit bewegen; im Falle von N 2müssen sich die Moleküle sogar zwanzigmal so schnell bewegen. Der Anteil der Moleküle, die sich mit einem Vielfachen der mittleren Geschwindigkeit bewegen, in generell äußerst gering, und weil sich dieser Anteil proportional zu e −v2verhält, wird er bei noch höheren Geschwindigkeiten rapide noch einmal kleiner. Ein winziger Anteil der He-Atome wird die Erdatmosphäre durchaus verlassen können, aber der Anteil noch schwererer Moleküle ist vernachlässigbar klein.
L1.2.1a
1 (i) Die mittlere Geschwindigkeit ist in Gl. (1.17) definiert als , also ist . Das Verhältnis der mittleren Geschwindigkeiten hängt daher vom Verhältnis der Molmassen ab:
2 (ii) Die mittlere kinetische Energie der Translation ist , wobei 〈v2〉 der Mittelwert des Quadrats der Geschwindigkeit ist; dieser ist in Gl. (1.15) mit 〈v2〉 = 3RT/M angegeben. Die mittlere kinetische Translationsenergie ergibt sich daher gemäßDie Molmasse M hängt mit der Masse m eines einzelnen Moleküls über M = mNA zusammen, wobei NA die Avogadro-Konstante ist. Für die Gaskonstante R können wir auch R = kNA schreiben, und somit giltWir erkennen, dass die mittlere kinetische Translationsenergie von der Identität des Gases unabhängig ist und ausschließlich von der Temperatur abhängt, d. h. sie ist für H2 und Hg identisch.Dieses Ergebnis steht im Zusammenhang mit dem Gleichverteilungssatz der Energie: ein Molekül besitzt drei Freiheitsgrade der Translation (x, y, und z), und jeder dieser Freiheitsgrade trägt zur mittleren Energie bei.
L1.2.2aDie quadratisch gemittelte Geschwindigkeit c ist durch Gl. (1.16) gegeben, c = (3 RT / M ) 1/2. Für H 2-Moleküle bei 20 °C erhalten wir
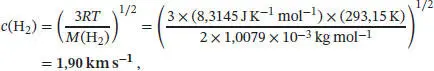
wobei wir 1 J = 1 kg m 2s −2verwendet und die Molmasse in kg mol −1angegeben haben.
Für O 2-Moleküle erhalten wir bei der gleichen Temperatur
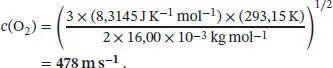
L1.2.3aDie Maxwell’sche Geschwindigkeitsverteilung, f ( v ), ist durch Gl. (1.12) gegeben. Der Anteil der Moleküle mit Geschwindigkeiten zwischen v 1und v 2ist durch das Integral
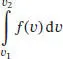
gegeben. Wenn der betrachtete Bereich v 2− v 1= δ v klein ist, wird die Lösung des Integrals in guter Näherung durch
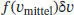
wiedergegeben, wobei v mittelder mittlere Wert des angegebenen Geschwindigkeitsbereichs ist: 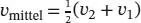 .
.
Im vorliegenden Fall ist v mittel= 205 m s −1und δ v = 10 ms −1. Der Anteil der N 2-Moleküle, die Geschwindigkeiten innerhalb des angegebenen Bereichs besitzen, ist daher
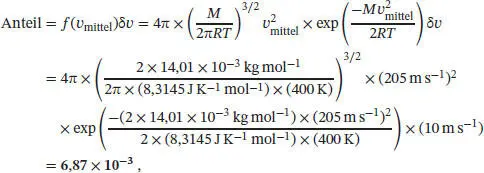
wobei wir 1 J = 1 kg m 2s −2verwendet haben. Dies bedeutet, dass sich 0,687 %der Moleküle mit Geschwindigkeiten innerhalb des angegebenen Bereichs bewegen.
L1.2.4aDie mittlere Relativgeschwindigkeit zweier verschiedener Moleküle in einem (idealen) Gas ist durch Gl. (1.19b) gegeben: 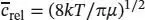 , wobei μ = m A m B/( m A+ m B) die reduzierte (effektive) Masse ist. Durch Multiplikation des Zählers und des Nenners mit der Avogadro-Konstante N Aund Substitution von N A k = R erhalten wir
, wobei μ = m A m B/( m A+ m B) die reduzierte (effektive) Masse ist. Durch Multiplikation des Zählers und des Nenners mit der Avogadro-Konstante N Aund Substitution von N A k = R erhalten wir
Читать дальше

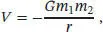
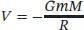
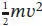 ; diese Geschwindigkeit entspricht der Fluchtgeschwindigkeit v e, wenn
; diese Geschwindigkeit entspricht der Fluchtgeschwindigkeit v e, wenn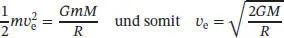
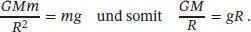
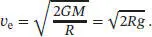
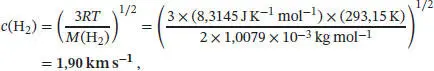
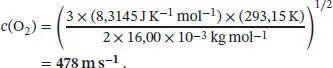
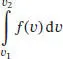
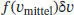
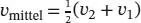 .
.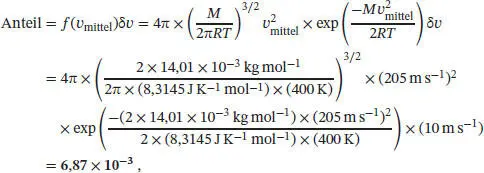
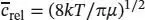 , wobei μ = m A m B/( m A+ m B) die reduzierte (effektive) Masse ist. Durch Multiplikation des Zählers und des Nenners mit der Avogadro-Konstante N Aund Substitution von N A k = R erhalten wir
, wobei μ = m A m B/( m A+ m B) die reduzierte (effektive) Masse ist. Durch Multiplikation des Zählers und des Nenners mit der Avogadro-Konstante N Aund Substitution von N A k = R erhalten wir










