James J. Keeler - Arbeitsbuch zu Atkins, de Paula, Keeler Physikalische Chemie

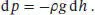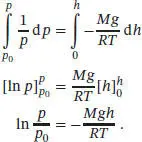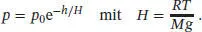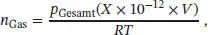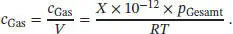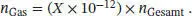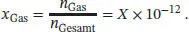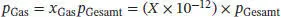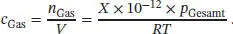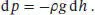
Das negative Vorzeichen wird benötigt, da sich der Druck mit zunehmender Höhe verringert.

Um den Zusammenhang zwischen der Dichte und dem Druck zu finden, gehen wir zunächst von der Zustandsgleichung des idealen Gases ( Gl. (1.4)) aus, pV = nRT. Wenn m die Masse des Gases und M seine Molmasse ist, folgt n = m/M und somit pV = ( m/M ) RT . Nun ziehen wir das Volumen auf die rechte Seite der Gleichung und erhalten p = ( m / MV ) RT . Der Quotient m/V entspricht der Dichte ρ (rho) des Gases, also gilt p = ( ρ/M ) RT ; dies lässt sich umstellen zu einem Ausdruck für die Dichte, ρ = Mp/RT .

Diesen Ausdruck für ρ setzen wir nun in die Beziehung d p = − ρg d h ein, und wir erhalten d p = −( Mp / RT ) g d h . Division durch p führt zur Variablentrennung: (1/ p ) d p = −( M / RT ) g d h . Die linke Seite dieser Gleichung integrieren wir nun zwischen p 0(dem Druck bei h = 0) und p (dem Druck in der Höhe h ). Die rechte Seite integrieren wir zwischen h = 0 und h :

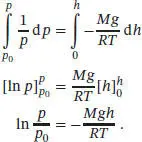
Nun bilden wir auf beiden Seiten e x, und es ergibt sich

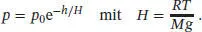
Wir wollen hier davon ausgehen, dass sich g und T bei Variation von h praktisch nicht ändern.

1 (a) Der Druck am oberen Ende des Gefäßes unterscheidet sich folglich praktisch nicht vom Druck am unteren Ende, da h/H ≪ 1 gilt. Wir können daher die Exponentialfunktion in eine Reihe entwickeln und nach den ersten beiden Termen abbrechen: ex ≈ 1 + x und somitNun stellen wir so um, dass wir einen Ausdruck für die Verminderung des Drucks, p−p0, erhalten,Wenn wir davon ausgehen, dass p0 dem einfachen Atmosphärendruck (1 atm) entspricht und laut Aufgabenstellung H = 8 km ist, erhalten wir für die Druckdifferenz

2 (b) Den Druck in einer Höhe von h = 11 km berechnen wir mithilfe des vollständigen Ausdrucks:

S1.1.13‡Wir betrachten ein Volumen V der Atmosphäre bei einer Temperatur T und dem Druck P Gesamt. Wenn die Konzentration eines in Spuren vorkommenden Gases als X „parts per trillion“ (ppt, billionstel Teile) angegeben wird, bedeutet dies: Wenn sich das Gas in einem Volumen X × 10 −12× V bei einer Temperatur T befindet, würde es einen Druck von p Gesamtausüben. Aus der Zustandsgleichung des idealen Gases folgt n = pV/RT , daher schreiben wir im vorliegenden Fall

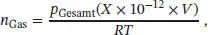
wobei n Gasdie Stoffmenge des in Spuren vorliegenden Gases ist. Wenn wir das Volumen V auf die linke Seite der Gleichung ziehen, erhalten wir für die (molare) Konzentration

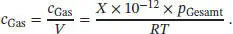
Ein alternativer Ansatz ist folgender: Bei einer gegebenen Temperatur und einem gegebenen Druck ist das vom Gas eingenommene Volumen proportional zu seiner Stoffmenge (in Mol). Wenn für das Gas X ppt angegeben wird, bedeutet dies, dass der Anteil X × 10 −12des Gesamtvolumens von diesem Gas eingenommen wird; die Stoffmenge dieses Gases ist also der Bruchteil X × 10 −12der insgesamt vorliegenden Stoffmenge (in Mol),

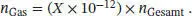
Durch Umstellen erhalten wir den Ausdruck für den Stoffmengenanteil (Molenbruch),

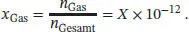
Der Partialdruck des in Spuren vorliegenden Gases ist daher

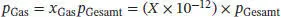
und seine Konzentration ist n Gas/ V = p Gas/ RT , also gilt

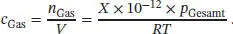
1 (a) Bei 10 °C und 1,0 atm erhalten wir:

2 (b) Bei 200 K und 0,050 atm erhalten wir:

D1.2.1Die drei Näherungen, die der kinetischen Gastheorie zugrunde liegen, sind in Abschn. 1.2.1 des Lehrbuchs genannt. Wir wollen sie hier noch einmal zusammenfassen:

1 Ein Gas besteht aus Molekülen, die sich in ständiger, ungerichteter Bewegung befinden, die den Gesetzen der klassischen Mechanik gehorcht.

2 Die Größe der Moleküle selbst ist vernachlässigbar klein in dem Sinne, dass ihre Durchmesser sehr viel kleiner sind als die mittlere Distanz, die ein Molekül zwischen zwei Stößen zurücklegt; die Moleküle werden gewissermaßen als „Punkte“ aufgefasst.

3 Die Moleküle interagieren nur während der kurzen, elastischen Stöße miteinander.

Als elastischen Stoß bezeichnet man eine Kollision, bei der die gesamte kinetische Energie der Moleküle erhalten bleibt.

Keine dieser drei Annahmen trifft uneingeschränkt zu; es handelt sich allerdings unter den meisten Bedingungen um gute Näherungen, insbesondere bei den üblicherweise vorliegenden Temperaturen und Drücken. Im Einzelnen sollten Sie allerdings beachten:

1 (a) Moleküle gehorchen den Gesetzen der Quantenmechanik; mit Ausnahme der leichtesten Gase bei extrem niedrigen Temperaturen fallen nicht-klassische Effekte bei diesen Betrachtungen jedoch kaum ins Gewicht.

2 (b) Mit zunehmendem Druck wird sich der mittlere Abstand zwischen den Molekülen immer weiter verringern, so dass schließlich die Abstände zwischen den Molekülen durchaus vergleichbar kleine Dimensionen annehmen wie die Moleküle selbst.

3 (c) Intermolekulare Wechselwirkungen, wie z. B. Wasserstoffbrückenbindungen oder die DipolDipol-Wechselwirkungen, fallen erst ins Gewicht, wenn sich die Moleküle in geringem Abstand zueinander befinden. Wenn als Folge davon Annahme (2) nicht mehr zutrifft, so wird alsbald auch Annahme (3) nicht mehr haltbar sein, da die Moleküle nun häufig nahe genug beieinander liegen, um miteinander in Wechselwirkung zu treten, ohne dass dabei ein Stoß stattfindet.

D1.2.3Damit ein Objekt (egal, ob es sich um ein Raumschiff oder um ein Molekül handelt) die Gravitation der Erde überwinden kann, muss es eine hinreichende kinetische Energie besitzen. Der Betrag der Energie muss mindestens der gravitationsbedingten potenziellen Energie des Objektes an der Erdoberfläche entsprechen. Das Gravitationspotenzial zwischen zwei Objekten mit den Massen m 1und m 2, die sich im Abstand r zueinander befinden, ist