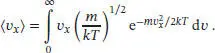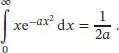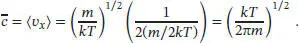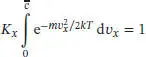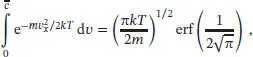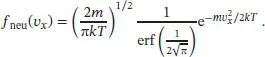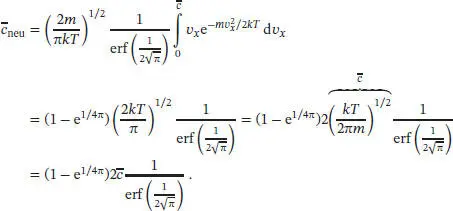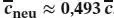1 ...7 8 9 11 12 13 ...43 Die Winkelgeschwindigkeit der Scheiben ist 2 πv rad s −1, sodass sich die Scheiben innerhalb einer Zeit t um einen Winkel von θ = 2 πvt drehen. Wenn wir den Abstand zwischen den einzelnen Scheiben mit d bezeichnen, wird ein Molekül mit der gerichteten Geschwindigkeit vx eine Zeit t = d/vx benötigen, um von einer Scheibe zur nächsten zu gelangen. Wenn der zweite Schlitz in einem Winkel α relativ zum ersten Schlitz liegt, wird das Molekül nur dann den zweiten Schlitz passieren können, wenn
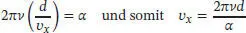
gilt. Wenn wir den Winkel α in Grad ausdrücken, mit α = π ( α °/180°), wird daraus
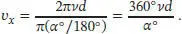
Mit den angegebenen Werten erhalten wir für die gerichtete Geschwindigkeit der Moleküle
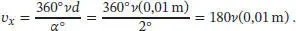
Die Maxwell’sche Geschwindigkeitsverteilung für ein eindimensionales System ist durch Gl. (1.11) gegeben:
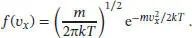
Wir nehmen an, dass die Angaben zur Intensität des Molekularstrahls zu dieser Verteilungsfunktion f ( vx ) proportional sind, I ∝ f ( vx ) = Af ( vx ). Da wir die Proportionalitätskonstante A nicht kennen und die Variation der Intensität mit vx untersucht werden soll, ist es an dieser Stelle hilfreich zu logarithmieren; wir erhalten
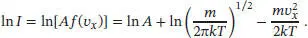
Bei einer Auftragung von ln I gegen sollte sich eine Gerade mit der Steigung − m/2kT ergeben; die entsprechende Wertetabelle sowie die grafische Auftragung ( Abb. 1.4) sind nachfolgend gezeigt.
| v /Hz |
Vx /m s −1 |
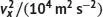 |
I (40 K) |
ln I (40 K) |
I (100 K) |
ln I (100 K) |
| 20 |
36 |
0,13 |
0,846 |
−0,167 |
0,592 |
−0,524 |
| 40 |
72 |
0,52 |
0,513 |
−0,667 |
0,485 |
−0,724 |
| 80 |
144 |
2,07 |
0,069 |
−2,674 |
0,217 |
−1,528 |
| 100 |
180 |
3,24 |
0,015 |
−4,200 |
0,119 |
−2,129 |
| 120 |
216 |
4,67 |
0,002 |
−6,215 |
0,057 |
−2,865 |
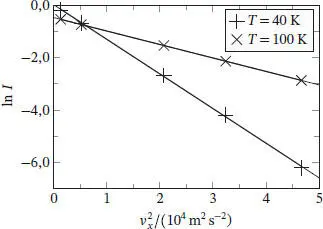
Abb. 1.4
Die Wertepaare liegen für die beiden untersuchten Temperaturen jeweils auf einer Geraden, mit einer Steigung von −1,33 bei 40 K bzw. −0,516 bei 100 K.
Um zu überprüfen, ob diese Daten durch eine Maxwell-Boltzmann-Verteilung beschrieben werden können, berechnen wir die theoretisch erwartete Steigung bei 40 K:
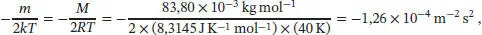
wobei wir R = N A k verwendet haben. Die erwartete Steigung ist daher −1,26, in recht guter Übereinstimmung mit dem experimentellen Wert.
Bei 100 K ist die theoretisch erwartete Steigung
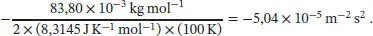
Wir sehen, dass auch in diesem Fall die theoretisch berechnete Steigung von −0,504 in guter Übereinstimmung zum experimentell ermittelten Wert steht.
S1.2.3Die Maxwell’sche Geschwindigkeitsverteilung für eindimensionale Systeme ist durch Gl. (1.11) gegeben,
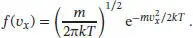
Zunächst formulieren wir unter Verwendung von Gl. (1.14), 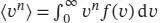 , einen Ausdruck für die mittlere Geschwindigkeit. Im hier vorliegenden Fall ist dies
, einen Ausdruck für die mittlere Geschwindigkeit. Im hier vorliegenden Fall ist dies
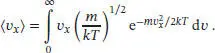
Zur Lösung des Integrals greifen wir auf das Standardintegral G2 aus dem Anhang des Lehrbuchs zurück:
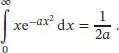
Mit a = m/2kT ergibt sich für die mittlere Geschwindigkeit
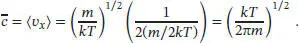
Nachdem der Molekularstrahl den Selektor passiert hat, ist f (vx) gleich null für alle vx > c̄ (Gasmoleküle mit diesen Geschwindigkeiten werden nicht durchgelassen). Die Wahrscheinlichkeitsverteilung wird dadurch verändert, und wir müssen die Funktion erneut normieren, sodass
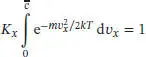
gilt. Dieses Integral lässt sich am einfachsten mithilfe mathematischer Software lösen; als Ergebnis erhalten wir
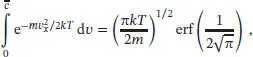
wobei erf( x ) die Fehlerfunktion ist. Die neu normierte Verteilungsfunktion lautet daher
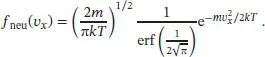
Auf dieser Grundlage lässt sich die neue mittlere Geschwindigkeit berechnen; auch in diesem Fall ist es hilfreich, hierfür mathematische Software zu nutzen. Beachten Sie, dass die mittlere Geschwindigkeit c̄ als neue obere Integrationsgrenze verwendet wird. Für die neue mittlere Geschwindigkeit erhalten wir
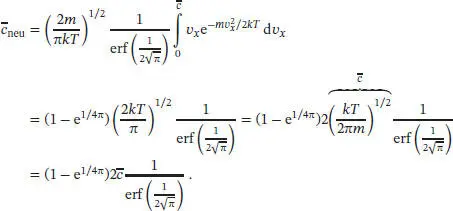
Die numerische Lösung der Fehlerfunktion lautet 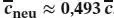
Читать дальше

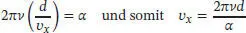
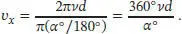
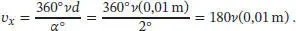
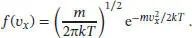
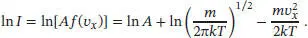
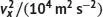

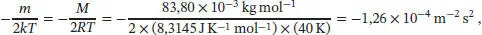
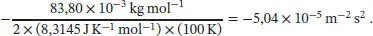
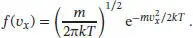
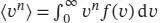 , einen Ausdruck für die mittlere Geschwindigkeit. Im hier vorliegenden Fall ist dies
, einen Ausdruck für die mittlere Geschwindigkeit. Im hier vorliegenden Fall ist dies