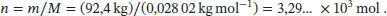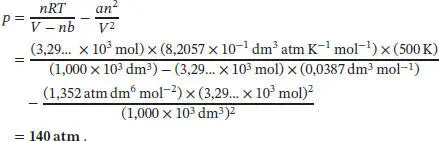Bei 300 K finden wir für Sauerstoff mit M (O 2) = 2 × 16,00 g mol −1einen Anteil von 0,0722, und bei 1000 K ist dieser Anteil 0,0134.
S1.2.11Die Stoßzahl z ist in Gl. (1.20b) mit 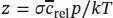 definiert, wobei die mittlere Relativgeschwindigkeit zweier Moleküle der gleichen Masse durch Gl. (1.19a),
definiert, wobei die mittlere Relativgeschwindigkeit zweier Moleküle der gleichen Masse durch Gl. (1.19a), 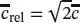 , und die mittlere Geschwindigkeit wiederum durch Gl. (1.17), c̄ = ( 8RT/nM ) 1/2, gegeben ist.
, und die mittlere Geschwindigkeit wiederum durch Gl. (1.17), c̄ = ( 8RT/nM ) 1/2, gegeben ist.
Zusammengefasst ergibt sich für die Stoßzahl
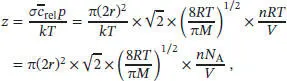
wobei wir die Beziehung R = N A k verwendet haben. Einsetzen der gegebenen Werte ergibt für die Stoßzahl der CH 4-Moleküle

1.3 Reale Gase
Diskussionsfragen
D1.3.1Wir betrachten drei unterschiedliche Temperaturbereiche:
1 T < TB : Bei sehr niedrigen Temperaturen zeigen alle Gase einen Kompressionsfaktor Z ≈ 1. Bei hohen Drücken ist Z > 1; das bedeutet, dass ihr molares Volumen größer ist als das molare Volumen eines idealen Gases; unter diesen Bedingungen sind abstoßende Wechselwirkungen dominant. Bei moderaten Drücken ist für die meisten Gase Z < 1; unter diesen Bedingungen sind anziehende Kräfte dominant, und das molare Volumen nimmt einen geringeren Wert an, als wir für ein ideales Gas erwarten würden.
2 T ≈ TB: Wenn der Druck gering ist, finden wir Z ≈ 1; bei moderaten Drücken liegt der Wert etwas unterhalb von 1, und bei hohen Drücken ist er deutlich größer als 1. Dies lässt darauf schließen, dass bei niedrigen bis moderaten Drücken ein Gleichgewicht zwischen anziehenden und abstoßenden Kräften existiert. Die abstoßenden Wechselwirkungen dominieren jedoch, sobald der Druck erhöht wird, denn die Gasmoleküle werden auf engem Raum sehr dicht zusammen gepresst.
3 T > TB: Unter diesen Bedingungen finden wir bei allen Drücken Z > 1, denn die Stoßfrequenz der Moleküle nimmt mit der Temperatur zu.
D1.3.3Die Van-der-Waals-Gleichung (Gl. (1.27a)) „korrigiert“ die Zustandsgleichung des idealen Gases ( Gl. (1.4)), indem sowohl anziehende als auch abstoßende Wechselwirkungen zwischen den Molekülen eines realen Gases berücksichtigt werden; in Abschn. 1.3.2 des Lehrbuchs finden Sie eine ausführlichere Erklärung.
Die Berthelot-Gleichung berücksichtigt das Eigenvolumen der Moleküle in ähnlicher Weise wie die Van-der-Waals-Gleichung; allerdings ist hier der Term, der die anziehenden Wechselwirkungen berücksichtigt, so modifiziert, dass der Einfluss der Temperatur ebenfalls berücksichtigt wird. Experimentell findet man, dass der Van-der-Waals-Parameter a mit steigender Temperatur kleiner wird. Auf der Grundlage theoretischer Überlegungen (siehe Fokus 14 des Lehrbuchs) würden wir ebenfalls erwarten, dass anziehende Wechselwirkungen zwischen den Molekülen mit steigender Temperatur schwächer werden. Diese Variation der anziehenden Wechselwirkungen mit der Temperatur wird in der Berthelot-Gleichung berücksichtigt, indem der Van-der-Waals-Parameter a durch a/T ersetzt wird.
L1.3.1aDie Van-der-Waals-Zustandsgleichung in Abhängigkeit vom Volumen ist in Gl. (1.27a) gegeben, p = nRT /( V − b ) − an 2/ V 2. Die Van-der-Waals-Koeffizienten a und b für Ethan sind in Tab. 1.6 im Anhang des Lehrbuchs mit a = 5,507 atm dm 6mol −2und b = 6,51 × 10 −2dm 3mol −1angegeben.
1 (i) Bei T = 273,15 K, V = 22,414 dm3, n = 1,0 mol ist der Druck
2 (ii) Bei T = 1000 K, V = 100 cm3 = 0,100 dm3, n = 1,0 mol ist der Druck
L1.3.2aWir benötigen folgende Umrechnungsfaktoren:
1 atm = 1,013 25 × 10 5Pa, 1 Pa = 1 kg m −1s −2, 1 dm 6= (10 −1m) 6= 10 −6m 6, 1 dm 3= 10 −3m 3. Folglich ist
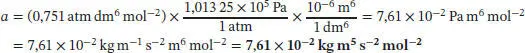
und

L1.3.3aWir verwenden die Definition 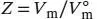 aus Gl. (1.23), wobei V mdas tatsächliche Molvolumen des Gases und
aus Gl. (1.23), wobei V mdas tatsächliche Molvolumen des Gases und 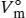 das Molvolumen des idealen Gases unter den gleichen Bedingungen ist. Dieses Volumen berechnen wir aus der Zustandsgleichung des idealen Gases, Gl (1.4), gemäß
das Molvolumen des idealen Gases unter den gleichen Bedingungen ist. Dieses Volumen berechnen wir aus der Zustandsgleichung des idealen Gases, Gl (1.4), gemäß 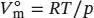 . Für den Kompressionsfaktor gilt Z = pV m/ RT (Gl. (1.24)).
. Für den Kompressionsfaktor gilt Z = pV m/ RT (Gl. (1.24)).
1 (i) Weil Vm um 12 % kleiner ist als das Molvolumen des idealen Gases, folgt . Nun können wir den Kompressionsfaktor Z direkt berechnen:
2 (ii) Aus Gl. (1.24) folgt Vm = ZRT/p. Das molare Volumen des Gases ist daherDer Kompressionsfaktor ist Z < 1. Wegen dominieren die anziehenden Kräfte.
L1.3.4aWir bestimmen zunächst die Stoffmenge des Gases aus seiner Masse, dann berechnen wir mithilfe der Van-der-Waals-Gleichung den Druck bei der herrschenden Temperatur. Die Anfangsbedingungen (300 K und 100 atm) sind für die Berechnung nicht notwendig.
Die Van-der-Waals-Zustandsgleichung in Abhängigkeit vom Volumen ist in Gl. (1.27a) gegeben, p = nRT /( V − b ) − an 2/ V 2. Die Molmasse von Stickstoff ist M (N 2) = 2 × 14,01 g mol −1= 28,02 g mol −1, und die Stoffmenge ist daher
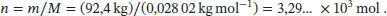
Zur Berechnung des Drucks verwenden wir nun Gl. (1.27a) und beachten dabei, das Volumen in der Einheit dm 3anzugeben ( V = 1,000 m 3= 1,000 × 10 3dm 3):
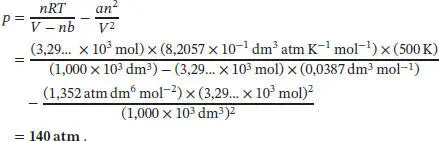
L1.3.5a
1 (i) Den Druck berechnen wir zunächst aus der Zustandsgleichung des idealen Gases Gl. (1.4), umgestellt nach p = nRT/V:
Читать дальше


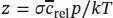 definiert, wobei die mittlere Relativgeschwindigkeit zweier Moleküle der gleichen Masse durch Gl. (1.19a),
definiert, wobei die mittlere Relativgeschwindigkeit zweier Moleküle der gleichen Masse durch Gl. (1.19a), 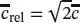 , und die mittlere Geschwindigkeit wiederum durch Gl. (1.17), c̄ = ( 8RT/nM ) 1/2, gegeben ist.
, und die mittlere Geschwindigkeit wiederum durch Gl. (1.17), c̄ = ( 8RT/nM ) 1/2, gegeben ist.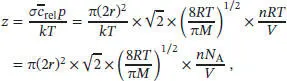

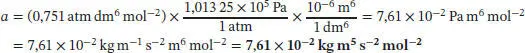

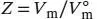 aus Gl. (1.23), wobei V mdas tatsächliche Molvolumen des Gases und
aus Gl. (1.23), wobei V mdas tatsächliche Molvolumen des Gases und 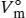 das Molvolumen des idealen Gases unter den gleichen Bedingungen ist. Dieses Volumen berechnen wir aus der Zustandsgleichung des idealen Gases, Gl (1.4), gemäß
das Molvolumen des idealen Gases unter den gleichen Bedingungen ist. Dieses Volumen berechnen wir aus der Zustandsgleichung des idealen Gases, Gl (1.4), gemäß 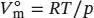 . Für den Kompressionsfaktor gilt Z = pV m/ RT (Gl. (1.24)).
. Für den Kompressionsfaktor gilt Z = pV m/ RT (Gl. (1.24)).