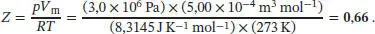2 (ii) Die Van-der-Waals-Zustandsgleichung in Abhängigkeit vom Volumen ist in Gl. (1.27a) gegeben, p = nRT/(V − b) − an2/V2. Wenn wir den Druck auf dieser Grundlage berechnen, erhalten wirDer Kompressionsfaktor Z in Abhängigkeit vom molaren Volumen und vom Druck ist durch Gl. (1.24) gegeben, Z = pVm/RT. Mit dem molaren Volumen Vm = V/n erhalten wir
L1.3.6aDie Beziehungen zwischen den kritischen Größen und den Van-der-Waals-Koeffizienten sind durch Gl. (1.28) gegeben:
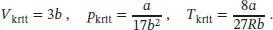
Alle drei kritischen Konstanten sind in der Aufgabenstellung angegeben, daher fällt uns die Lösung nicht schwer: jedes beliebige Paar dieser Beziehungen ist hinreichend, um die Werte von a und b zu berechnen. Es ist nützlich, für die Gaskonstante R = 8,2057 × 10 −2dm 3atm K −1mol −1zu verwenden und die Volumina in der Einheit dm 3anzugeben.
Wenn wir beispielsweise die Beziehungen für V kritund p kritverwenden, lassen sich die Van-der-Waals-Koeffizienten wie folgt bestimmen:

Insgesamt haben wir drei verschiedene Möglichkeiten, zwei der oben genannten Beziehungen zur Bestimmung von a und b heranzuziehen, wobei wir allerdings jedes Mal abweichende Werte erhalten. Für den Van-der-Waals-Parameter a erhalten wir die Zahlenwerte 1,33, 1,74 bzw. 2,26, und somit einen Mittelwert von 1,78 atm dm6 mol−2. Für den Van-der-Waals-Parameter b erhalten wir die Zahlenwerte 0,0329, 0,0329 bzw. 0,0429, und somit einen Mittelwert von 0,0362 dm3 mol−1.
In Abschn. 1.3.2a des Lehrbuchs wird erklärt, dass b = 4 V Molekül N Agilt, wobei V Moleküldas durch ein einzelnes Molekül eingenommene Volumen ist. Wenn wir die Moleküle näherungsweise als kugelförmig annehmen, können wir dieses Volumen über den Radius r als 4 πr 3/3 ausdrücken, und es folgt r = (3 b /16 πN A) 1/3. Mithilfe dieser Beziehung und dem zuvor bestimmten Mittelwert von b erhalten wir für den Radius der Moleküle
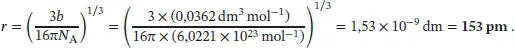
L1.3.7a
1 (i) In Abschn. 1.3.1b des Lehrbuchs haben wir erklärt, dass bei der Boyle-Temperatur Z = 1 und dZ/dp = 0 ist; die letztgenannte Bedingung ergibt sich daraus, dass der zweite Virialkoeffizient B bei dieser Temperatur null wird: B = 0. Unsere Aufgabe besteht nun zunächst darin, eine Beziehung zwischen den Van-der-Waals-Koeffizienten und den Virialkoeffizienten zu finden. Ausgangspunkt hierfür sind die Ausdrücke für das Produkt pVm, die wir aus den Gln. (1.27b) und (1.25b) erhalten:Den Ausdruck für pVm aus der Van-der-Waals-Gleichung stellen wir nun um, indem wir den Zähler und den Nenner des ersten Terms durch Vm dividieren; wir erhaltenSo lange b/Vm ≪ 1 ist, können wir die Reihenentwicklung (1 − x)−1 ≈ 1 + x ansetzen. Das ergibtIn dieser Form der Gleichung identifizieren wir den zweiten Virialkoeffizienten B alsgilt. Da bei der Boyle-Temperatur B = 0 = b − a/RTB gilt, folgt TB = a/Rb. Für Chlor entnehmen wir aus Tab. 1.6 im Anhang des Lehrbuchs a = 6,260 dm6 atm mol−2 und b = 0,0542 dm3 mol−1. Damit erhalten wir
2 (ii) In Abschn. 1.3.2a des Lehrbuchs wird erklärt, dass b = 4VMolekülNA gilt, wobei VMolekül das durch ein einzelnes Molekül eingenommene Volumen ist. Wenn wir die Moleküle näherungsweise als kugelförmig annehmen, können wir dieses Volumen über den Radius r als 4πr3/3 ausdrücken, und es folgt r = (3b/16πNA)1/3. Für den Radius von Cl2-Molekülen erhalten wir damit
L1.3.8aReduzierte Variablen werden in Abhängigkeit von den kritischen Größen definiert, siehe Gl. (1.30):
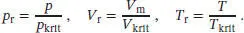
Wenn der reduzierte Druck für zwei Gase (1) und (2) identisch ist, folgt
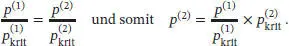
In analoger Weise folgt für die Temperatur
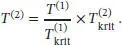
Diese Beziehungen können wir nun verwenden, um den Druck und die Temperatur des Gases (2) zu berechnen, dessen Zustand dem eines Gases (1) entspricht (d. h. „korrespondiert“); hierzu müssen uns allerdings die kritischen Größen beider beteiligter Gase bekannt sein.
1 (i) Aus Tab. 1.5 im Anhang des Lehrbuchs entnehmen wir für Wasserstoff pkrit = 12,8 atm, Tkrit = 33,23 K, und für Ammoniak pkrit = 111,3 atm, Tkrit = 405,5 K. Wennwir H2 als Gas (1) und NH3 als Gas (2) bezeichnen, lassen sich der Druck und die Temperatur von Ammoniak, die dem Zustand p(H2) = 1,0atm und T(H2) = 298,15 K von Wasserstoffgas entsprechen, wie folgt berechnen:
2 (ii) Aus Tab. 1.5 im Anhang des Lehrbuchs entnehmen wir für Xenon pkrit = 58,0 atm und Tkrit = 289,75 K. Also ist
3 (iii) Aus Tab. 1.5 im Anhang des Lehrbuchs entnehmen wir für Helium pkrit = 2,26 atm und Tkrit = 5,21 K. Also ist
L1.3.9aDie Van-der-Waals-Zustandsgleichung in Abhängigkeit vom molaren Volumen ist in Gl. (1.27b) gegeben, 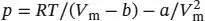 . Wir lösen nach b auf und erhalten
. Wir lösen nach b auf und erhalten
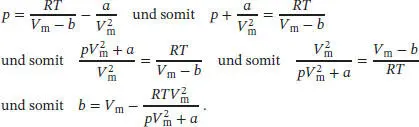
Einsetzen der Werte ergibt
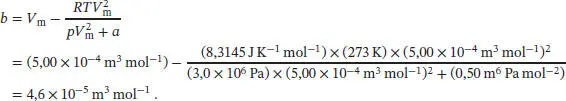
Dabei haben wir 1 Pa = 1 kg m −1s −2und 1 J = 1 kg m 2s −2verwendet.
Der Kompressionsfaktor Z ist in Gl. (1.23) als 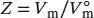 definiert, wobei V mdas tatsächliche Molvolumen ist und
definiert, wobei V mdas tatsächliche Molvolumen ist und 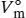 das Molvolumen des idealen Gases unter den gleichen Bedingungen. Dieses Volumen berechnen wir aus der Zustandsgleichung des idealen Gases, Gl. (1.4), gemäß
das Molvolumen des idealen Gases unter den gleichen Bedingungen. Dieses Volumen berechnen wir aus der Zustandsgleichung des idealen Gases, Gl. (1.4), gemäß 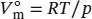 . Für den Kompressionsfaktor gilt Z = pV m/ RT (Gl. (1.24)). Einsetzen der Werte ergibt
. Für den Kompressionsfaktor gilt Z = pV m/ RT (Gl. (1.24)). Einsetzen der Werte ergibt
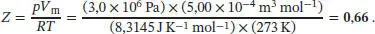 Читать дальше
Читать дальше

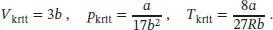

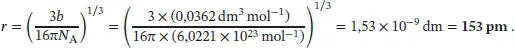
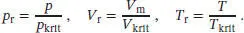
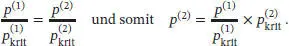
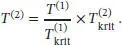
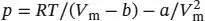 . Wir lösen nach b auf und erhalten
. Wir lösen nach b auf und erhalten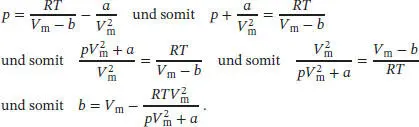
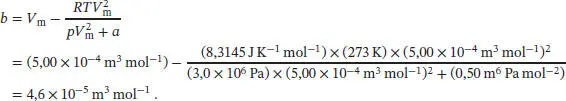
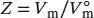 definiert, wobei V mdas tatsächliche Molvolumen ist und
definiert, wobei V mdas tatsächliche Molvolumen ist und 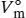 das Molvolumen des idealen Gases unter den gleichen Bedingungen. Dieses Volumen berechnen wir aus der Zustandsgleichung des idealen Gases, Gl. (1.4), gemäß
das Molvolumen des idealen Gases unter den gleichen Bedingungen. Dieses Volumen berechnen wir aus der Zustandsgleichung des idealen Gases, Gl. (1.4), gemäß 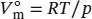 . Für den Kompressionsfaktor gilt Z = pV m/ RT (Gl. (1.24)). Einsetzen der Werte ergibt
. Für den Kompressionsfaktor gilt Z = pV m/ RT (Gl. (1.24)). Einsetzen der Werte ergibt