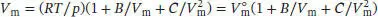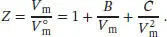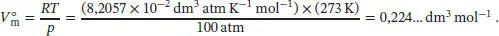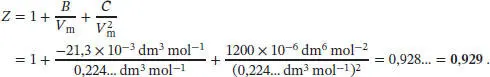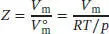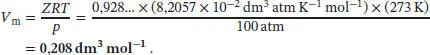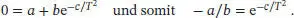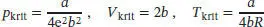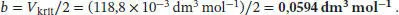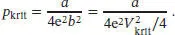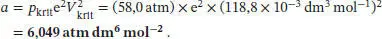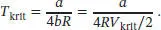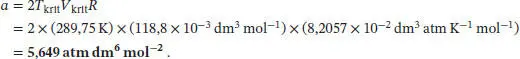S1.3.1Die Virialgleichung ist in Gl. (1.25b) gegeben, pV m= RT (1 + B/V m+ …). Aus Tab. 1.4 im Anhang des Lehrbuchs entnehmen wir für N 2bei 273 K den zweiten Virialkoeffizienten B = −10,5 cm 3mol −1. Die Molmasse von Stickstoff ist M (N 2) = 2 × 14,01 gmol −1= 28,02 g mol −1, daher ist das molare Volumen der Gasprobe
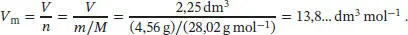
Mithilfe dieses Wertes und der Virialgleichung können wir nun den Druck berechnen. Es ist nützlich, für die Gaskonstante R = 8,2057 × 10 −2dm 3atm K −1mol −1zu verwenden und die Volumina in der Einheit dm 3anzugeben. Wir erhalten
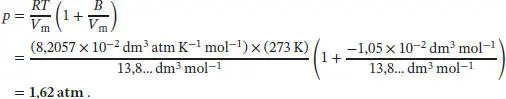
S1.3.3Die Virialgleichung (Gl. (1.25b)) lautet 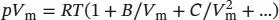 . Der Kompressionsfaktor Z ist in Gl. (1.23) als
. Der Kompressionsfaktor Z ist in Gl. (1.23) als 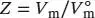 definiert, wobei V mdas tatsächliche molare Volumen ist und
definiert, wobei V mdas tatsächliche molare Volumen ist und 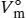 das molare Volumen des idealen Gases unter den gleichen Bedingungen; es gilt
das molare Volumen des idealen Gases unter den gleichen Bedingungen; es gilt 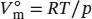 .
.
Daraus folgt
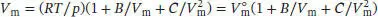
und somit für den Kompressionsfaktor
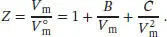
Um diesen Ausdruck zu evaluieren, verwenden wir näherungsweise das molare Volumen des idealen Gases unter den gleichen Bedingungen für das molare Volumen des realen Gases; wir erhalten
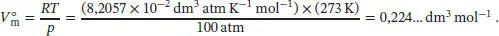
Diesen Wert für das molare Volumen verwenden wir nun zur Berechnung des Kompressionsfaktors Z ; beachten Sie, dass wir hierzu alle Volumina in die Einheit dm 3umgerechnet haben:
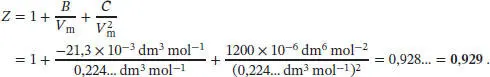
Das molare Volumen können wir nun mithilfe des Kompressionsfaktors berechnen:
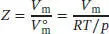
und somit
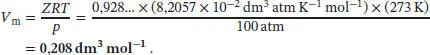
S1.3.5‡In Abschn. 1.3.1b des Lehrbuchs haben wir erklärt, dass bei der Boyle-Temperatur Z = 1 und d Z /d p = 0 ist; die letztgenannte Bedingung ergibt sich daraus, dass der zweite Virialkoeffizient B bei dieser Temperatur null wird: B = 0. Die Boyle-Temperatur lässt sich ermitteln, indem wir den Ausdruck für B(T) gleich null setzen und nach T auflösen:
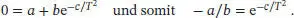
Durch Logarithmieren erhalten wir ln(− a/b ) = − c / T 2und somit durch Einsetzen der Werte für die Boyle-Temperatur von Methan

S1.3.7
1 (a) Die Molmasse von H2O istM(H2O) = 18,02 g mol−1. Die Dichte p hängt mit der molaren Dichte ρm über ρm = ρ/M zusammen, und das molare Volumen Vm entspricht dem Kehrwehrt dieser Größe, Vm = 1/ρm=M/ρ.Das molare Volumen des Wasserdampfs ist also 0,1353 dm3 mol−1.
2 (b) Der Kompressionsfaktor Z ist durch Gl. (1.24), Z =pVm/RT, gegeben. Einsetzen der Werte sowie des molaren Volumens Vm aus Teilaufgabe (a) liefert
3 (c) Die Virialgleichung (bis einschließlich des zweiten Terms) in Abhängigkeit vom molaren Volumen ist durch Gl. (1.25b) gegeben:Nach Division durch p auf beiden Seiten der Gleichung ergibt sichDie Größe RT/p identifizieren wir als das molare Volumen eines idealen Gases, , und damit folgtIn der Lösung zu Aufgabe L1.3.7ahaben wir gezeigt, dass der Virialkoeffizient B mit den Van-der-Waals-Koeffizienten a und b über B = b − a/RT zusammenhängt. Diese Beziehung verwenden wir nun zur Bestimmung von B, und das Ergebnis zur Berechnung des Kompressionsfaktors Z:
S1.3.9Gemäß Tab. 1.7 des Lehrbuchs sind die kritischen Größen für die Dieterici-Zustandsgleichung durch
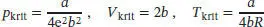
gegeben. Aus Tab. 1.5 im Anhang des Lehrbuchs entnehmen wir die folgenden Werte für Xenon: T krit= 289,75 K, p krit= 58,0 atm, V krit= 118,8 cm 3mol −1. Den Koeffizienten b können wir direkt mithilfe des Wertes von V kritberechnen,
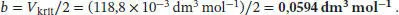
Nun Kombinieren wir die Ausdrücke für p kritund V krit, um b zu eliminieren,
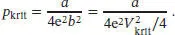
Durch Umstellen dieser Beziehung lässt sich nun der Koeffizient a berechnen,
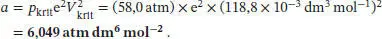
Alternativ dazu können wir auch die Ausdrücke für T kritund V kritkombinieren, um b zu eliminieren,
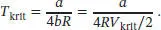
Durch Umstellen dieser Beziehung lässt sich nun der Koeffizient a berechnen,
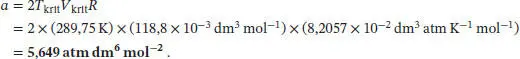
Wir erkennen sofort, dass die beiden berechneten Werte für a nicht identisch sind; der Mittelwert beträgt 5,849 atm dm 6mol −2.
Читать дальше

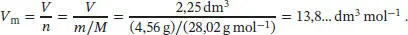
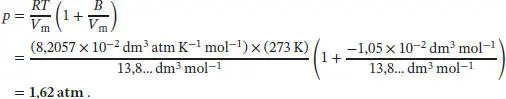
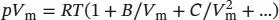 . Der Kompressionsfaktor Z ist in Gl. (1.23) als
. Der Kompressionsfaktor Z ist in Gl. (1.23) als 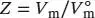 definiert, wobei V mdas tatsächliche molare Volumen ist und
definiert, wobei V mdas tatsächliche molare Volumen ist und 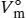 das molare Volumen des idealen Gases unter den gleichen Bedingungen; es gilt
das molare Volumen des idealen Gases unter den gleichen Bedingungen; es gilt 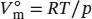 .
.