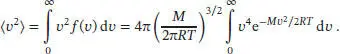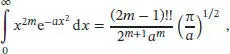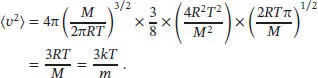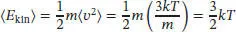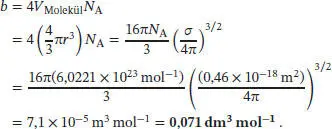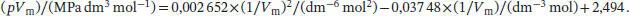
Der Koeffizient des Terms mit (1/ V m) 2entspricht CRT :
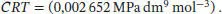
Wie zuvor in Teilaufgabe (a) konvertieren wir der Bequemlichkeit halber den Druck in die Einheit atm, wodurch wir CRT = (0,026 17 atm dm 9mol −3) erhalten; somit ist der dritte Virialkoeffizient
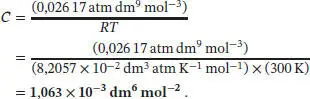
S1.3.23Die Van-der-Waals-Gleichung in Abhängigkeit vom molaren Volumen ist durch Gl. (1.27b) gegeben, 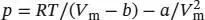 . Dies ist eine kubische Gleichung in V m, was spätestens deutlich wird, wenn wir sie auf beiden Seiten mit
. Dies ist eine kubische Gleichung in V m, was spätestens deutlich wird, wenn wir sie auf beiden Seiten mit 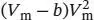 multiplizieren und die Terme zusammenfassen:
multiplizieren und die Terme zusammenfassen:
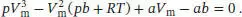
Aus Tab. 1.6 im Anhang des Lehrbuchs entnehmen wir die Van-der-Waals-Parameter von Cl 2,
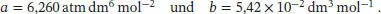
Der Bequemlichkeit halber konvertieren wir den angegebenen Druck in die Einheit atm,
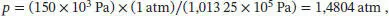
und verwenden R = 8,2057 × 10 −2dm 3atm K −1mol −1; nun setzen wir alle diese Werte sowie die in der Aufgabenstellung angegebene Temperatur ein; dadurch erhalten wir folgendes Polynom:
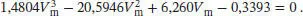
Die Lösungen dieses Polynoms lassen sich am einfachsten mithilfe mathematischer Software bestimmen. Die einzige physikalisch sinnvolle Lösung für das molare Volumen ist Vm= 13, 6 dm3 mol −1.
Das molare Volumen eines idealen Gases bei denselben Bedingungen ist
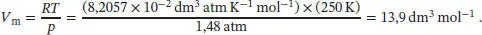
Wir sehen, dass das Volumen des Van-der-Waals-Gases etwa 2 % geringer ist als wir es für ein ideales Gas erwarten.
Abschnittsübergreifende Aufgaben
A1.1Die Maxwell-Boltzmann-Verteilung der Molekülgeschwindigkeiten in drei Dimensionen ist durch Gl. (1.12) gegeben:
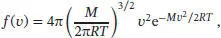
wobei M die Molmasse ist. Die wahrscheinlichste Geschwindigkeit kann gefunden werden, indem wir die Ableitung von f(v) nach v bilden und gleich null setzen; zur Berechnung dieser Ableitung müssen wir die Kettenregel beachten:
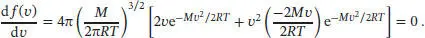
Die Konstanten und die Faktoren von v und 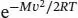 können wir vernachlässigen (denn diese entsprechen keinen Maxima), und es verbleibt
können wir vernachlässigen (denn diese entsprechen keinen Maxima), und es verbleibt

Wenn wir uns die Form der Verteilungskurve ansehen, stellen wir fest, dass sich an dieser Stelle ein Maximum befindet.
Die mittlere kinetische Energie lässt sich aus dem Mittelwert des Quadrats der Geschwindigkeit berechnen, 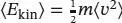 Die Aufgabe besteht nun darin, diesen Mittelwert mithilfe der Maxwell- Boltzmann-Verteilung zu berechnen; das hierfür benötigte Integral ist
Die Aufgabe besteht nun darin, diesen Mittelwert mithilfe der Maxwell- Boltzmann-Verteilung zu berechnen; das hierfür benötigte Integral ist
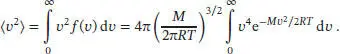
Dieses Integral hat die gleiche Form wie das Standardintegral G8 aus dem Anhang des Lehrbuchs:
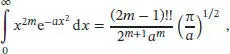
mit m = 2, (2 m − 1)!! = 3 × 1 = 3, 2 m+1=8, am = a 2und a = M/2RT. Der Mittelwert des Quadrats der Geschwindigkeit ist
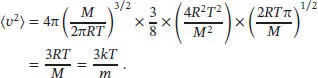
Für die Umformung im vorletzten Schritt dieser Gleichung ist eine Reihe sorgfältig ausgeführter algebraischer Berechnungen bzw. Umstellungen nötig; im letzten Schritt haben wir R = N A k und M = mN Averwendet, wobei m die Masse des Moleküls ist.
Mit diesem Ergebnis können wir
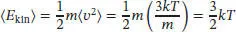
schreiben, was im Einklang mit dem Gleichverteilungssatz steht.
A1.3In Abschn. 1.3.2a des Lehrbuchs wird erklärt, dass b = 4 V Molekül N Agilt, wobei V Moleküldas durch ein einzelnes Molekül eingenommene Volumen ist. Der Stoßquerschnitt σ ist in Abhängigkeit eines Stoßdurchmessers d definiert als σ = πd 2, und für den Durchmesser wird wiederum der doppelte Radius der stoßenden Kugeln angenommen: d = 2 r . Daraus folgt, mit r = ( σ /4 π ) 1/2
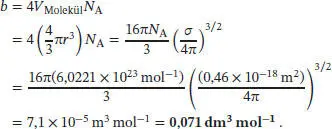
FOKUS 2
Der Erste Hauptsatz der Thermodynamik
Behandeln Sie alle Gase als ideal, sofern nicht ausdrücklich etwas anderes verlangt ist. Thermochemische Daten sind für 298,15 K angegeben, sofern nicht ausdrücklich etwas anderes erwähnt ist.
Die mit dem Symbol ‡ gekennzeichneten Aufgaben wurden von Charles Trapp und Carmen Giunta beigesteuert.
Читать дальше

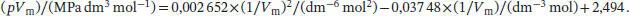
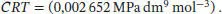
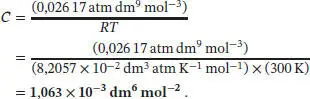
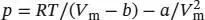 . Dies ist eine kubische Gleichung in V m, was spätestens deutlich wird, wenn wir sie auf beiden Seiten mit
. Dies ist eine kubische Gleichung in V m, was spätestens deutlich wird, wenn wir sie auf beiden Seiten mit 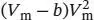 multiplizieren und die Terme zusammenfassen:
multiplizieren und die Terme zusammenfassen: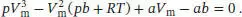
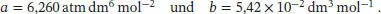
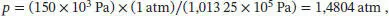
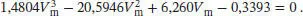
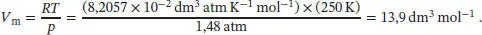
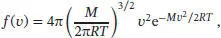
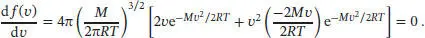
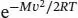 können wir vernachlässigen (denn diese entsprechen keinen Maxima), und es verbleibt
können wir vernachlässigen (denn diese entsprechen keinen Maxima), und es verbleibt
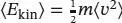 Die Aufgabe besteht nun darin, diesen Mittelwert mithilfe der Maxwell- Boltzmann-Verteilung zu berechnen; das hierfür benötigte Integral ist
Die Aufgabe besteht nun darin, diesen Mittelwert mithilfe der Maxwell- Boltzmann-Verteilung zu berechnen; das hierfür benötigte Integral ist