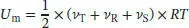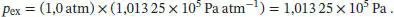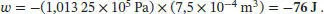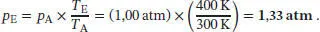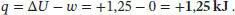James J. Keeler - Arbeitsbuch zu Atkins, de Paula, Keeler Physikalische Chemie

D2.1.1In der Physikalischen Chemie teilen wir das Universum in zwei gedachte, voneinander getrennte Bereiche auf: das System und seine Umgebung. In der Thermodynamik bezeichnen wir den uns interessierenden Teil des Universums als System, das von seiner Umgebung durch „Wände“ oder allgemein eine bestimmte Art von Begrenzung separiert ist. Die Eigenschaften dieser Wände bestimmen, ob es sich um ein offenes, ein geschlossenes oder ein abgeschlossenes (isoliertes) System handelt.

Ein offenes System ist von Wänden umgeben, die sowohl den Austausch von Materie als auch von Energie zulassen. Die Wände eines geschlossenen Systems erlauben lediglich den Austausch von Energie, nicht jedoch von Materie. Geschlossene Systeme können entweder adiabatisch oder diathermisch sein. In adiabatischen Systemen findet keine Energieübertragung aufgrund des Vorliegens einer Temperaturdifferenz statt, bei diathermischen Systemen ist dies jedoch möglich. Die Wände eines abgeschlossenen ( isolierten ) Systems erlauben weder den Austausch von Materie noch von Energie zwischen dem System und der Umgebung.

D2.1.3In Tab. 2.1 in Abschn. 2.1.3a des Lehrbuchs sind vier unterschiedliche Arten von Arbeit aufgelistet: Volumenarbeit, Oberflächenarbeit, Längenausdehnung und elektrische Arbeit. Darüber hinaus existiert eine Form der Arbeit, die mit Prozessen in Magnet- und Gravitationsfeldern assoziiert ist, auf die wir an dieser Stelle jedoch nicht näher eingehen.

D2.1.5Die isotherme Expansion eines Gases kann technisch bewerkstelligt werden, indem dafür gesorgtwird, dass das Gas und sein Behälter in thermischem Kontakt mit einem großen Reservoir stehen (z. B. mit einem Wasserbad), dessen Temperatur konstant gehalten wird – dies nennt man einen Thermostaten .

L2.1.1aIn „Toolkit 7: Der Gleichverteilungssatz“ in Abschn. 2.1.2a des Lehrbuchs wird der Gleichverteilungssatz erläutert. Die molare Innere Energie ist durch

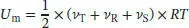
gegeben, wobei v T, v Rund v Sdie Anzahl der Translations-, Rotations- bzw. der Schwingungsfreiheitsgrade ist. Jedes Gasmolekül kann sich frei entlang der drei Raumrichtungen x , y und z bewegen, daher ist die Anzahl der Translationsfreiheitsgrade v T= 3.

1 (i) Molekulares Iod ist ein zweiatomiges Molekül und besitzt daher zwei Rotationsfreiheitsgrade. Aufgrund seiner sehr schweren Atome können wir anzunehmen, dass molekulares Iod (I2) bei Raumtemperatur nur einen einzigen Schwingungsfreiheitsgrad besitzt. Die molare Innere Energie von gasförmigem Iod bei Raumtemperatur ist somit

2 (ii) und (iii) Sowohl das tetraedrische Methanmolekül (CH4) als auch das planare Benzolmolekül (C6 H6) besitzen drei Rotationsfreiheitsgrade. Bei Zimmertemperatur ist es unwahrscheinlich, dass eine der Schwingungsmoden angeregt ist; wir können daher davon ausgehen, dass diese beiden Moleküle bei 25 °C ähnliche Innere Energien besitzen:

L2.1.2aEine Zustandsfunktion beschreibt eine Größe, deren Wert ausschließlich vom momentanen Zustand des Systems abhängig ist; auf welchem Wege dieser Zustand erreicht worden ist, spielt dabei keine Rolle. Druck, Temperaturund Enthalpiesind Zustandsfunktionen; die Arbeit hingegen nicht.

L2.1.3aDie Expansion vollzieht sich gegen einen konstanten äußeren Druck. Nach Gl. (2.6) gilt w = − p exΔ V , also ist der äußere Druck

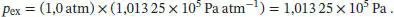
Die Volumenänderung ergibt sich als Querschnittsfläche mal der linearen Verschiebung:

Mit diesen beiden Werten sowie 1 Pa = 1kg m −1s −2und 1 J = 1kgm 2s −2ergibt sich für die verrichtete Volumenarbeit

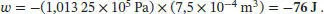
L2.1.4aIn allen drei Fällen ist Δ U = 0, weil die Innere Energie eines idealen Gases nur von der Temperatur abhängt (eine ausführlichere Diskussion finden Sie in den Abschn. 2.1.2 und 2.4.2 des Lehrbuchs). Aus der Definition der Enthalpie folgt H = U + pV und damit Δ H = Δ U + Δ( pV ) = Δ U + Δ( nRT ); die letzte Gleichung gilt für ein ideales Gas. Damit ist für alle Vorgänge in einem idealen Gas auch Δ H = 0,wenn die Temperatur konstant bleibt. Somit gilt für alle drei Prozesse Δ U = Δ H = 0.

1 (i) Die bei einer reversiblen isothermen Expansion eines idealen Gases verrichtete Arbeit ist durch Gl. (2.9) gegeben,Beachten Sie, dass bei dieser Berechnung die Temperatur in der Einheit Kelvin (K) angegeben wird. Nach dem Ersten Hauptsatz der Thermodynamik ist

2 (ii) Der Enddruck des expandierenden Gases, pE, lässt sich aus der Zustandsgleichung idealer Gase ( Gl. (1.4), pV = nRT) berechnen:Dies entspricht dem konstanten äußeren Druck pex, gegen den sich das Gas ausdehnt; die verrichtete Volumenarbeit ist daherund somit ist q =+1,62 kJ

3 (iii) Eine freie Expansion vollzieht sich ohne Kraftaufwand, also ist w = 0 und somit auch q = ΔU − w = 0 − 0 = 0.

L2.1.5aBei konstantem Volumen gilt für ein ideales Gas p A/ T A= p E/ T E, also ist

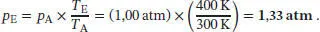
Die Änderung der Inneren Energie ist durch Gl. (2.15b) gegeben,

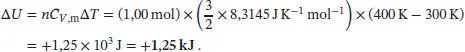
Das Volumen des Gases ist konstant, daher ist die verrichtete Volumenarbeit w = 0. Damit folgt nach dem Ersten Hauptsatz

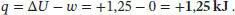
L2.1.6a

1 (i) Die Volumenarbeit gegen einen konstanten äußeren Druck ist durch Gl. (2.6) gegeben:Beachten Sie, dass bei Verwendung dieser Gleichung der Druck in der Einheit Pascal (Pa) und die Volumenänderung in Kubikmetern (m3) angegeben werden müssen, um die Arbeit in der Einheit Joule (J) zu erhalten.

2 (ii) Die bei einer reversiblen isothermen Expansion verrichtete Arbeit ist durch Gl. (2.9) gegeben, w = −nRT ln(VE/VA). Die Stoffmenge des Methangases istund für die Volumenarbeit erhalten wirBeachten Sie, dass der Betrag der verrichteten Arbeit bei einem reversiblen Prozessverlauf größer ist als bei der (irreversiblen) Expansion des Gases gegen einen konstanten äußeren Druck.

S2.1.1Nach dem Gleichverteilungssatz (siehe „Toolkit 7: Der Gleichverteilungssatz“ in Abschn. 2.1des Lehrbuchs) ist die molare Innere Energie durch