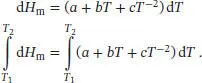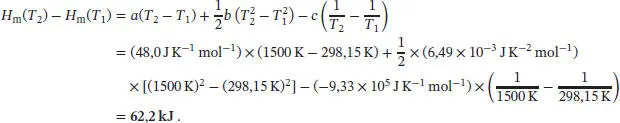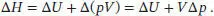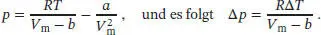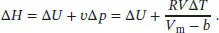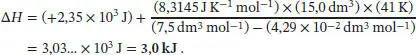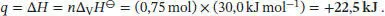L2.2.4aAus Gl. (2.23) folgt
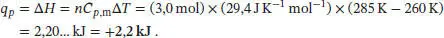
Gemäß Gl. (2.18b) gilt bei konstantem Druck q p= ΔH, also ist ΔH = + 2, 2kJ.
Die Enthalpie ist in Gl. (2.17) definiert, H = U + pV. Für eine Enthalpieänderung bei konstantem Druck folgt ΔH = ΔU + pΔV mit Δ V = V E − V A . Wenn wir ein ideales Gas betrachten, gilt V E= nRT E/ p und V A= nRT A/ p, und die Volumenänderung ist somit Δ V = (T E − T A )nR / p . Es folgt p Δ V = nR(T E − T A ) = nR Δ T, und die Änderung der Inneren Energie eines idealen Gases ist daher

S2.2.1Eine Masse von 10 g Benzol entspricht einer Stoffmenge von n = m / M = (10 g)/ (78,1074 g mol −1) = 0,128… mol. Die benötigte Wärmemenge, um 10 g dieser Substanz bei konstantem Druck zu verdampfen, ist q p= n × Δ V H m= (0,128. mol) × (30,8 kJ mol −1) = 3,94… kJ. Ein elektrischer Strom mit der Stromstärke I, der entlang einer Potenzialdifferenz Δϕ fließt, entspricht einer Leistung von IΔϕ Wenn dieser Strom für einen Zeitraum von Δt aufrecht erhalten wird, ergibt sich die Energie aus dem Produkt Leistung × Zeit, also q = IΔϕΔt. Damit erhalten wir
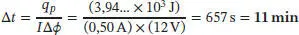
(mit 1A = 1Cs −1und 1V = 1JC −1).
S2.2.3Mithilfe mathematischer Software passen wir die gegebenen Daten an einen Ausdruck mit der allgemeinen Form 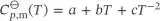 an; für die drei Parameter erhalten wir a = 48,0JK −1mol −1, b = 6,49 × 10 −3JK −2mol −1und c = −9,33 × 10 5JK −1mol −1. Die molare Enthalpieänderung, die sich bei konstantem Druck durch eine Änderung der Temperatur ergibt, ist durch Gl. (2.22a) gegeben, d H m = Cp , md T. Einsetzen dieser Beziehung in den Ausdruck für Cp , mund Integration auf beiden Seiten der resultierenden Gleichung liefert
an; für die drei Parameter erhalten wir a = 48,0JK −1mol −1, b = 6,49 × 10 −3JK −2mol −1und c = −9,33 × 10 5JK −1mol −1. Die molare Enthalpieänderung, die sich bei konstantem Druck durch eine Änderung der Temperatur ergibt, ist durch Gl. (2.22a) gegeben, d H m = Cp , md T. Einsetzen dieser Beziehung in den Ausdruck für Cp , mund Integration auf beiden Seiten der resultierenden Gleichung liefert
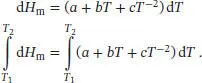
Zur Lösung verwenden das Standardintegral A1 aus dem Anhang des Lehrbuchs, und es folgt
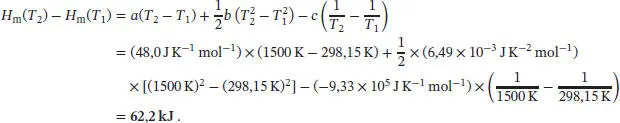
S2.2.5Das Volumen bleibt konstant, also ist w = 0(d. h., es wird keine Volumenarbeit verrichtet). Weil aber bei konstantem Volumen Δ U = q gilt, folgt Δ U = q V= + 2, 35 kJ. Wegen Δ V = 0 ist
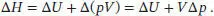
Nach der Van-der-Waals-Gleichung (Gl. (1.27b)) ist
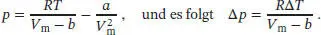
Beachten Sie, dass sich der Term, der den Parameter a enthält, herauskürzt, da das Volumen konstant gehalten wird. Also ist
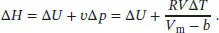
Mit den angegebenen Werten erhalten wir V m= V / n = (15,0 dm 3)/(2,0 mol) = 7,5 dm 3mol −1sowie Δ T = 341K − 300 K = 41K, und aus Tab. 1.6 des Lehrbuchs entnehmen wir den Van-der-Waals-Koef-fizienten b = 4,29 × 10 −2dm 3mol −1. Also ist die Enthalpieänderung
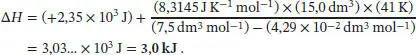
2.3 Thermochemie
Diskussionsfragen
D2.3.1Die Verdampfung von Wasser ist ein endothermer Phasenübergang: H 2O (l) → H 2O (g), Δ V H ⊖= +44,01 kJ mol −1. Daher muss für die Verdampfung der Flüssigkeit Energie in Form von Wärme zugeführt werden. Diese Energieübertragung kühlt sowohl die Stoffstreifen als auch die Luftmoleküle in ihrer unmittelbaren Umgebung ab.
D2.3.3Der Standardzustandeiner Substanz ist ihre reine Form bei einem Druck von 1 bar und einer gegebenen Temperatur. Für den Standardzustand ist keine bestimmte Temperatur vorgegeben; wenn wir allerdings Werte für thermodynamische Standardgrößen angeben sollen, dann gehen wir
üblicherweise von der Raumtemperatur von 298,15 K (25 °C) aus. Der Referenzzustandeiner Substanz ist ihr stabilster Zustand bei einem Druck von 1 bar und einer gegebenen Temperatur. Diese Unterscheidung ist wichtig, denn Bildungsenthalpien beziehen sich auf die Bildung einer Substanz aus ihren Elementen, die in ihren jeweiligen Referenzzuständen vorliegen – bei anderen Arten von Angaben zu Reaktionen ist es möglich, dass eine Substanz nicht in ihrem Referenzzustand vorliegt.
Die Unterscheidung zwischen dem Standardzustand und dem Referenzzustand eines chemischen Elements mag auf den ersten Blick marginal erscheinen; bei Elementen, die bei einer bestimmten Temperatur in unterschiedlichen Formen vorliegen können, wird der Sinn dieser Differenzierung jedoch deutlich: Ein Element kann mehr als einen Standardzustand besitzen – einer für jede Form, in der dieses Element bei einer bestimmten Temperatur vorliegt.
Standardzustände bilden einen Fixpunkt in der Thermodynamik, auf dessen Grundlage wir eine thermodynamische Größe unter anderen Bedingungen berechnen können (z. B. bei Drücken, die vom Standarddruck 1 bar deutlich abweichen). Anhand tabellierter thermodynamischer Daten zu den Standardzuständen können wir diese Größen bei anderen Bedingungen ableiten, ohne jedes Mal eine neue, für diese Bedingungen spezifische Liste erstellen zu müssen.
Durch die Angabe der Referenzzustände ist es möglich, konsistente Datentabellen aufzustellen, die untereinander jederzeit vergleichbar sind.
L2.3.1aTetrachlormethan wird bei konstantem Druck verdampft, daher gilt
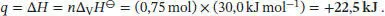
Die bei konstantem Druck verrichtete Arbeit ist durch Gl. (2.6) gegeben, w = − p exΔ V . Beachten Sie, dass näherungsweise Δ V = V Egilt, denn die Substanz nimmt im gasförmigen Endzustand ein viel größeres Volumen als im flüssigen Anfangszustand. Das Endvolumen V Elässt sich mithilfe der Zustandsgleichung des idealen Gases ( Gl. (1.4)) berechnen.
Читать дальше

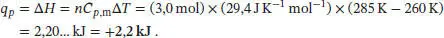

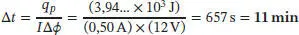
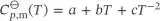 an; für die drei Parameter erhalten wir a = 48,0JK −1mol −1, b = 6,49 × 10 −3JK −2mol −1und c = −9,33 × 10 5JK −1mol −1. Die molare Enthalpieänderung, die sich bei konstantem Druck durch eine Änderung der Temperatur ergibt, ist durch Gl. (2.22a) gegeben, d H m = Cp , md T. Einsetzen dieser Beziehung in den Ausdruck für Cp , mund Integration auf beiden Seiten der resultierenden Gleichung liefert
an; für die drei Parameter erhalten wir a = 48,0JK −1mol −1, b = 6,49 × 10 −3JK −2mol −1und c = −9,33 × 10 5JK −1mol −1. Die molare Enthalpieänderung, die sich bei konstantem Druck durch eine Änderung der Temperatur ergibt, ist durch Gl. (2.22a) gegeben, d H m = Cp , md T. Einsetzen dieser Beziehung in den Ausdruck für Cp , mund Integration auf beiden Seiten der resultierenden Gleichung liefert