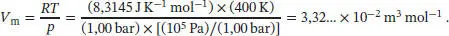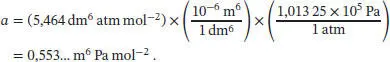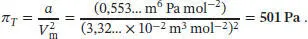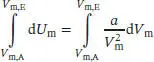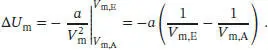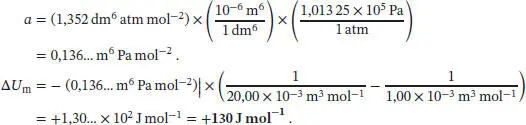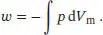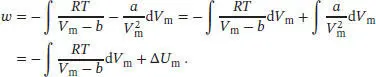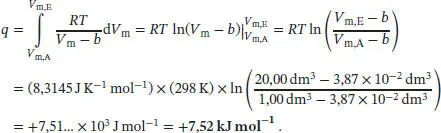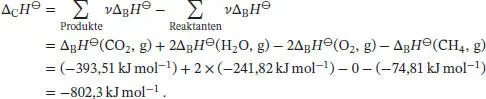
Die Temperaturabhängigkeit der Standardreaktionsenthalpie ist durch das Kirchhoff’sche Gesetz (Gl. (2.32a)) gegeben:
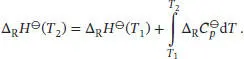
Die Differenz der molaren Wärmekapazitäten der Produkte und der Reaktanten lässt sich mithilfe von Gl. (2.32b) berechnen:
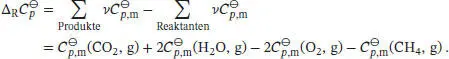
Die molaren Wärmekapazitäten bei konstantem Druck werden in der Form 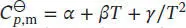 angegeben, daher schreiben wir
angegeben, daher schreiben wir 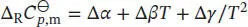 mit Δα = α(CO 2, g) + 2α(H 2O, g) − 2α(O 2, g) − α(CH 4, g). In analoger Weise lassen sich entsprechende Beziehungen für Δ β und Δ γ formulieren. So erhalten wir:
mit Δα = α(CO 2, g) + 2α(H 2O, g) − 2α(O 2, g) − α(CH 4, g). In analoger Weise lassen sich entsprechende Beziehungen für Δ β und Δ γ formulieren. So erhalten wir:
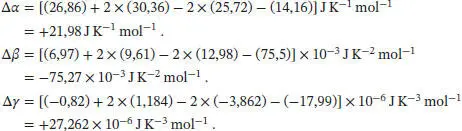
Durch Integration des Kirchhoff’sehen Gesetzes erhalten wir

S2.3.11
1 (a) Die bei der Verbrennung von Glucose freigesetzte Wärmemenge beträgtDie Innere Energie dieser Verbrennungsreaktion beträgtDie Reaktionsgleichung für die Verbrennung von Glucose istDa sich die Stoffmenge der an der Reaktion beteiligten Gase nicht ändert, gilt gemäß Gl. (2.20) ΔCU⊖ = ΔCH⊖ = −2,80… × 103 kJ mol−1 = −2,80 × 103 kJ mol−1. Die Standardbildungsenthalpie ΔBH⊖ von Glucose berechnen wir mithilfe von Gl. (2.30a) unter Verwendung der thermochemischen Daten, die in Tab. 2.11 im Anhang des Lehrbuchs angegeben sind:
2 (b) Die Reaktionsgleichung für die anaerobe Oxidation von Glucose zu Milchsäure istFür die Standardreaktionsenthalpie erhalten wirWir erkennen, dass bei der aeroben Oxidation deutlich mehr Energie freigesetzt wird als bei der anaeroben Oxidation; die Differenz beträgt
2.4 Zustandsfunktionen und totale Differenziale
Diskussionsfrage
D2.4.1In Abschn. 3.5.1(b) des Lehrbuchs wird erklärt, dass der Binnendruck eines Van-der-Waals-Gases durch die Beziehung 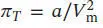 gegeben ist. Dieser Binnendruck ist definiert als π T= (∂ U /∂ V)T ; diese Größe gibt daher an, wie sich bei konstanter Temperatur die Innere Energie in Abhängigkeit vom Volumen ändert. Der Van-der-Waals-Parameter a ist stets positiv – dies bedeutet, dass die Innere Energie bei der Expansion eines Gases grundsätzlich zunimmt. Die molekulare Interpretation hierfür ist, dass die anziehenden Wechselwirkungen zwischen den Gasmolekülen bei einer Vergrößerung des Volumens immer weniger ins Gewicht fallen.
gegeben ist. Dieser Binnendruck ist definiert als π T= (∂ U /∂ V)T ; diese Größe gibt daher an, wie sich bei konstanter Temperatur die Innere Energie in Abhängigkeit vom Volumen ändert. Der Van-der-Waals-Parameter a ist stets positiv – dies bedeutet, dass die Innere Energie bei der Expansion eines Gases grundsätzlich zunimmt. Die molekulare Interpretation hierfür ist, dass die anziehenden Wechselwirkungen zwischen den Gasmolekülen bei einer Vergrößerung des Volumens immer weniger ins Gewicht fallen.
Der Binnendruck verhält sich umgekehrt proportional zum molaren Volumen: je größer das Molvolumen wird, desto größer wird auch der Abstand zwischen den Molekülen, wodurch die Auswirkungen der (anziehenden) intermolekularen Wechselwirkungen mehr und mehr an Bedeutung verlieren, bis sie schließlich vernachlässigbar sind.
L2.4.1aDas molare Volumen eines idealen Gases bei 400 K ist
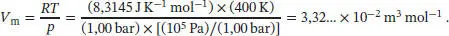
Wir entnehmen den Van-der-Waals-Parameter a von Wasserdampf aus Tab. 1.6 in Abschn. 1.3des Lehrbuchs und rechnen den angegebenen Wert in SI-Einheiten um:
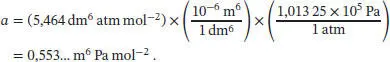
Der Binnendruck von Wasserdampf bei 1,00 bar und 400 K ist daher
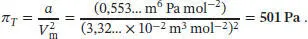
L2.4.2aDie (molare) Innere Energie eines geschlossenen Systems ist eine Funktion der Temperatur und des Volumens, U m= U m( T , V m). Mithilfe von Gl. (2.39), d U = πT d V + Cv d T , können wir d U für jede beliebige Änderung von V und/oder T berechnen. Bei konstant gehaltener Temperatur vereinfacht sich diese Gleichung zu dU = π TdV. Einsetzen dieser Beziehung in den Ausdruck für den Binnendruck π Teines Van-der-Waals-Gases liefert (mit molaren Größen)

Wenn wir diesen Ausdruck zwischen V m,Aund V m,Eintegrieren, erhalten wir
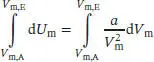
und somit
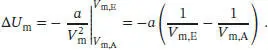
Wir entnehmen den Van-der-Waals-Parameter a von gasförmigem Stickstoff aus Tab. 1.6 in Abschn. 1.3des Lehrbuchs und rechnen den angegebenen Wert in SI-Einheiten um:
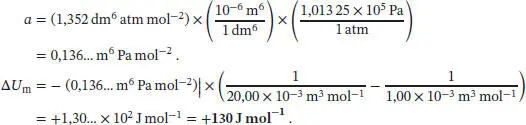
Die Arbeit, die durch Expansion eines Gases verrichtet wird, ist durch Gl. (2.5a) gegeben, d w = − p exd V . Bei einer reversiblen Expansion entspricht der äußere Druck p exdem Druck p des Gases, und somit gilt
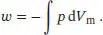
Diesen Ausdruck setzen wir in die Beziehung für den Druck eines Van-der-Waals-Gases ein (Gl. (2.30b)):
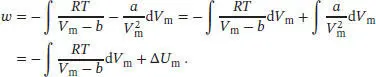
Den zweiten Term aus der ersten Zeile identifizieren wir als die Größe Δ U m. Nach dem Ersten Hauptsatz der Thermodynamik gilt Δ U = q + w , und der erste Term in obigem Ausdruck muss demnach −q entsprechen. Daher ist
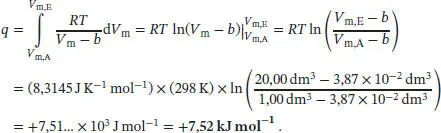
Den Wert des Van-der-Waals-Koeffizienten b haben wir aus Tab. 1.6 im Anhang des Lehrbuchs entnommen. Nach dem Ersten Hauptsatz entspricht die verrichtete Arbeit w = −q + Δ U m, und wir erhalten
Читать дальше

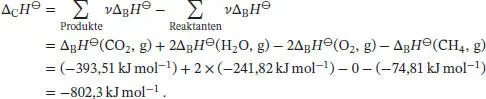
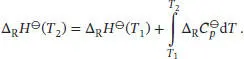
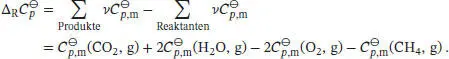
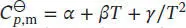 angegeben, daher schreiben wir
angegeben, daher schreiben wir 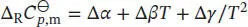 mit Δα = α(CO 2, g) + 2α(H 2O, g) − 2α(O 2, g) − α(CH 4, g). In analoger Weise lassen sich entsprechende Beziehungen für Δ β und Δ γ formulieren. So erhalten wir:
mit Δα = α(CO 2, g) + 2α(H 2O, g) − 2α(O 2, g) − α(CH 4, g). In analoger Weise lassen sich entsprechende Beziehungen für Δ β und Δ γ formulieren. So erhalten wir: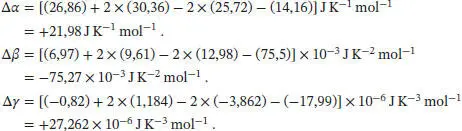

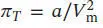 gegeben ist. Dieser Binnendruck ist definiert als π T= (∂ U /∂ V)T ; diese Größe gibt daher an, wie sich bei konstanter Temperatur die Innere Energie in Abhängigkeit vom Volumen ändert. Der Van-der-Waals-Parameter a ist stets positiv – dies bedeutet, dass die Innere Energie bei der Expansion eines Gases grundsätzlich zunimmt. Die molekulare Interpretation hierfür ist, dass die anziehenden Wechselwirkungen zwischen den Gasmolekülen bei einer Vergrößerung des Volumens immer weniger ins Gewicht fallen.
gegeben ist. Dieser Binnendruck ist definiert als π T= (∂ U /∂ V)T ; diese Größe gibt daher an, wie sich bei konstanter Temperatur die Innere Energie in Abhängigkeit vom Volumen ändert. Der Van-der-Waals-Parameter a ist stets positiv – dies bedeutet, dass die Innere Energie bei der Expansion eines Gases grundsätzlich zunimmt. Die molekulare Interpretation hierfür ist, dass die anziehenden Wechselwirkungen zwischen den Gasmolekülen bei einer Vergrößerung des Volumens immer weniger ins Gewicht fallen.