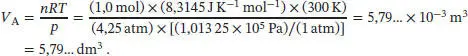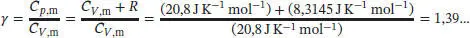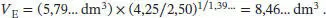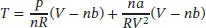
und somit ist
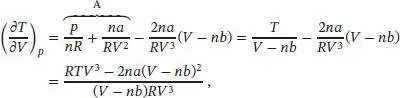
wobei wir den mit A bezeichneten Term mithilfe der vorangegangenen Gleichung als T/ ( V − nb ) identifizieren. Unter Verwendung der Kehrwert-Identität können wir auch schreiben:
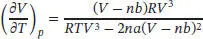
und somit
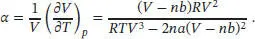
Es folgt
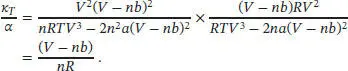
Für eine molare Größe geht V → Vm und n → 1 , und wir erhalten κ T/α = ( Vm − b ) /R bzw. nach Umstellen κTR = α(Vm − b).
S2.4.7‡Umstellen der Zustandsgleichung für das beschriebene Gas nach dem Volumen ergibt
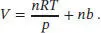
Daraus folgt
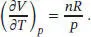
Einsetzen dieses Ergebnisses in den Ausdruck für den Joule-Thomson-Koeffizienten μ . liefert
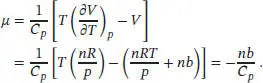
Die Wärmekapazität und der Van-der-Waals-Parameter b sind stets positiv, daher ist der Koeffizient μ für dieses Gas negativ. Demnach muss, wenn der Druck bei einer (isenthalpen) Joule-Thomson-Expansion fällt, die Temperatur steigen.
S2.4.9‡Nach Gl. (2.47) ist dH = − μCp d p + Cp d T. Bei konstanter Temperatur gilt daher
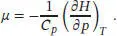
Die partielle Ableitung (∂ H/ ∂ pT ) entspricht der Steigung einer Auftragung von H gegen p bei konstanter Temperatur.
1 (a) In Abb. 2.2ist die Auftragung der gegebenen Daten für 300 K gezeigt.Die Steigung der Geraden ist −17,93. Damit können wir den Joule-Thomson-Koeffizienten berechnen:
2 (b) In Abb. 2.3ist die Auftragung der gegebenen Daten für 350 K gezeigt.Die Steigung der Geraden ist −14,46. Damit können wir den Joule-Thomson-Koeffizienten berechnen: Abb. 2.2 Abb. 2.3
2.5 Adiabatische Änderungen
Diskussionsfrage
D2.5.1Bei einer adiabatischen Expansion wird dem System keine Energie in Form von Wärme zugeführt; daher nimmt der Druck im Vergleich zu einer isothermen Expansion schneller ab, denn bei der adiabatischen Expansion verringert sich die Temperatur.
L2.5.1aBei Ammoniak und Methan handelt es sich um nichtlineare mehratomige Moleküle; sie besitzen daher jeweils drei Freiheitsgrade der Translation und drei Freiheitsgrade der Rotation. Nach dem Gleichverteilungssatz (siehe „Toolkit 7: Der Gleichverteilungssatz“ in Abschn. 2.1des Lehrbuchs) gilt
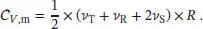
Hierbei bezeichnen v T, v Rund v Sdie Anzahl der Freiheitsgrade der Translation, der Rotation bzw. der Schwingung.
1 (i) Die Berechnung von γ ohne Berücksichtigung des Schwingungsbeitrags liefert für beide Moleküle das gleiche Ergebnis, . Für ein ideales Gas gilt gemäß Gl. (2.25) CP,m = CV,m + R, und somit
2 (ii) Wenn wir den Schwingungsbeitrag berücksichtigen, unterscheiden sich die Werte von γ für die beiden Moleküle. Die Zahl der Schwingungsmoden für ein nichtlineares mehratomiges Molekül ist vS = 3N − 6, wobei N die Anzahl der Atome ist. Für Ammoniak ergibt sich daher vS = 3N − 6 = 6 und für Methan vS = 3N − 6 = 9. Für die Wärmekapazitäten von Ammoniak erhalten wir und Cp,m(NH3) = 10R, und somity . Für Methan erhalten wir und Cp,m(CH4) = 13R, und somit .Die experimentell ermittelten Werte von y für Ammoniak und Methan sind identisch, γ = 1,31. Dieser Wert liegt näher an dem berechneten Wert ohne Berücksichtigung des Schwingungsbeitrags.
L2.5.2aBei einer reversiblen adiabatischen Expansion gilt nach Gl. (2.49a), ( T E/ T A) = ( V A/ V E) 1/cmit c = CV ,m/ R . Für ein einatomiges ideales Gas gilt 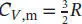 und somit
und somit 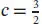 . Damit ist die gesuchte Endtemperatur des Gases
. Damit ist die gesuchte Endtemperatur des Gases
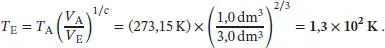
L2.5.3aIn einem adiabatischen Prozess hängen Anfangs- und Enddruck gemäß Gl. (2.50) zusammen, 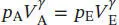 , wobei γ das Verhältnis der Wärmekapazitäten ist, γ = Cp ,m/ C v,m. Aus der Zustandsgleichung des idealen Gases erhalten wir für das Anfangsvolumen
, wobei γ das Verhältnis der Wärmekapazitäten ist, γ = Cp ,m/ C v,m. Aus der Zustandsgleichung des idealen Gases erhalten wir für das Anfangsvolumen
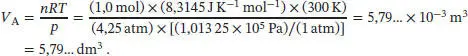
Für ein ideales Gas gilt gemäß Gl. (2.25) Cp , m– CV , m= R , und somit
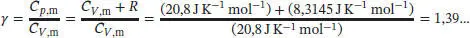
Das Endvolumen ist gegeben durch
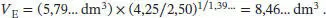
Somit ist V E= 8. 46 dm3.
Bei einer reversiblen adiabatischen Expansion gilt nach Gl. (2.49a), ( T E/ T A) = ( V A/ V E) 1/cmit c = CV , m/ R . Für das vorliegende Gas ist c = (20.8 JK −1mol −1)/(8.3145 JK −1mol −1) = 2.50… , und somit ist die Endtemperatur
Читать дальше

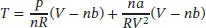
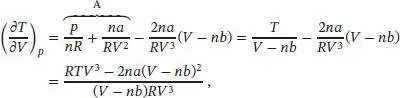
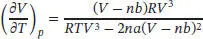
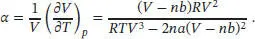
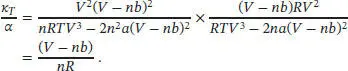
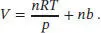
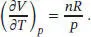
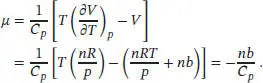
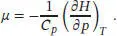
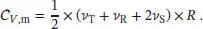
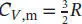 und somit
und somit 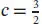 . Damit ist die gesuchte Endtemperatur des Gases
. Damit ist die gesuchte Endtemperatur des Gases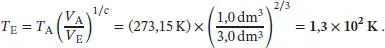
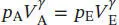 , wobei γ das Verhältnis der Wärmekapazitäten ist, γ = Cp ,m/ C v,m. Aus der Zustandsgleichung des idealen Gases erhalten wir für das Anfangsvolumen
, wobei γ das Verhältnis der Wärmekapazitäten ist, γ = Cp ,m/ C v,m. Aus der Zustandsgleichung des idealen Gases erhalten wir für das Anfangsvolumen