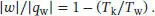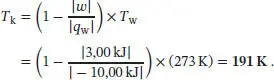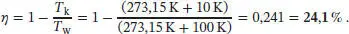James J. Keeler - Arbeitsbuch zu Atkins, de Paula, Keeler Physikalische Chemie

2 (ii) Isotherme irreversible Expansion gegen pex = 0:Die Entropie ist eine Zustandsfunktion, und da die Anfangs- und Endzustände des Systems mit denjenigen aus Teilaufgabe (a) identisch sind, gilt auch für den irreversiblen FallBei einer Expansion gegen einen äußeren Druck von pex = 0 wird keine Arbeit verrichtet, und für den isothermen Prozess eines idealen Gases ist ∆U = 0. Aus dem Ersten Hauptsatz der Thermodynamik folgt, dass q = 0 und somit ∆SUmg = 0 sein muss. Damit ist

3 (iii) Reversible adiabatische Expansion:Bei einer adiabatischen Expansion findet zwischen dem System und der Umgebung keine Wärmeübertragung statt, daher ist ∆SUmg = 0. Für einen reversiblen Prozess gilt ∆Sges = 0, daher muss auch ∆S = 0 sein.

L3.1.5aDer Wirkungsgrad einer Wärmekraftmaschine ist in Gl. (3.7) definiert, η = | ω |/| q w|, und für einen Carnot-Kreisprozess gilt gemäß Gl. (3.9) η = 1 − ( T k/ T w). Wenn wir diese beiden Gleichungen kombinieren und geeignet umstellen, erhalten wir in einen Ausdruck für die Temperatur der Wärmesenke:

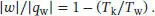
Damit erhalten wir im vorliegenden Fall

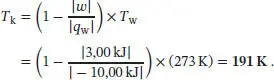
L3.1.6aDer Wirkungsgrad eines Carnot-Kreisprozesses ist in Gl. (3.9) definiert, η = 1 − ( T k/ T w). Im vorliegenden Fall ergibt sich

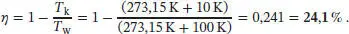
Beachten Sie, dass die Temperatur in der Einheit Kelvin (K) angegeben werden muss.

S3.1.1

1 (a) Isotherme reversible Expansion:Die bei einer reversiblen isothermen Expansion eines idealen Gases verrichtete Arbeit ist durch Gl. (2.9) gegeben, w = − nRT ln(VE/VA). Da bei konstanter Temperatur gemäß dem Gesetz von Boyle p ∝ (1/V) gilt, lautet ein äquivalenter AusdruckFür den isothermen Prozess eines idealen Gases ist ∆U = 0 und ∆H = 0. Der Erste Hauptsatz der Thermodynamik ist in Gl. (2.2) gemäß ∆U = q + ω definiert; damit erhalten wirDie Wärmeübertragung verläuft reversibel, daher ist qrev = q. Für die Entropieänderung ergibt sichDer Prozess soll insgesamt reversibel sein, daher muss ∆Sges = 0 gelten. Mit ∆Sges = ∆S + ∆SUmg erhalten wir schließlich

2 (b) Isotherme Expansion gegen einen konstanten äußeren Druck von pex = 1,00 atm:Die verrichtete Volumenarbeit bei der Expansion eines idealen Gases gegen einen konstanten Druck ist durch Gl. (2.6) gegeben, ω = − pex(VE − VA). Die Volumina lassen sich mithilfe der Zustandsgleichung des idealen Gases ( Gl. (1.4), pV = nRT) auch über die Drücke angeben. Die verrichtete Arbeit ist somitFür den isothermen Prozess eines idealen Gases ist ∆U = 0 und ∆H = 0. Der Erste Hauptsatz der Thermodynamik ist in Gl. (2.2) gemäß ∆U = q + ω definiert; damit erhalten wirDie Entropie ist eine Zustandsfunktion, und da die Anfangs- und Endzustände des Systems identisch sind, gilt wie in Teilaufgabe (a) für die Entropieänderung ∆S = + 9, 13 JK -1.Die Entropieänderung der Umgebung in Abhängigkeit von der Wärme der Umgebung, qUmg, ist durch Gl. (3.2b) gegeben, ∆S = qUmg/T. Diese Wärmemenge entspricht gerade dem Negativen der Wärme des Systems, qUmg = − q. Damit erhalten wir

S3.1.3

1 (a) Nach Schritt 1 des Carnot-Kreisprozesses verdoppelt sich das Volumen des Gases, daher ist VB = 2 × VA = 2 × (1,00 dm3) = 2,00 dm3. Wenn wir für die adiabatischen Schritte VT 3/2 = konstant annehmen, wie in der Aufgabenstellung erwähnt, dann ist das Volumen nach Schritt 2

2 (b) Wenn wir für die adiabatischen Schritte erneut VT 3/2 = konstant voraussetzen, können wir das Volumen des Gases nach Schritt 3 aus dem Anfangsvolumen vor Beginn des Kreisprozesses berechnen:

3 (c) In Abschn. 3.1.3a des Lehrbuchs wird gezeigt, dass die reversibel übertragene Wärmemenge bei isothermer Expansion eines Gases durch qrev = nRT ln(VE/VA) gegeben ist. Die Wärmemengen, die in den Schritten 1 bzw. 3 des Kreisprozesses übertragen werden, sind daherDa bei einem adiabatischen Prozess keine Wärmeübertragung zwischen System und Umgebung stattfindet, sind die Wärmemengen für Schritt 2 und 4 gleich null, also q2 = 0 und q4 = 0.

4 (d) Die Temperatur zu Beginn und am Ende des Kreisprozesses muss identisch sein. Da ein ideales Gas als Arbeitsmedium verwendet wird, giltüber den gesamten Kreisprozess ∆U = 0. Nach dem Ersten Hauptsatz der Thermodynamik gilt ∆U = ω+q (Gl. (2.2)); somit muss ω = −q sein. Dies bedeutet, dass die insgesamt während des Kreisprozesses übertragene Wärmemenge in Arbeit umgewandelt wird. Diese Nettowärmemenge ergibt sich aus der Differenz zwischen der Wärmemenge, die der Wärmequelle entnommen wurde, und der Wärmemenge, die an die Wärmesenke abgegeben wird.

5 (e) Der Wirkungsgrad einer Wärmekraftmaschine ist in Gl. (3.7) definiert, η = | ω |/| qw|. Wie in Teilaufgabe (d) erwähnt, entspricht | ω | der insgesamt während des Kreisprozesses übertragenen Wärmemenge. Im vorliegenden Fall ergibt sichund der Wirkungsgrad η ist somit

6 (f) Der Wirkungsgrad eines Carnot-Kreisprozesses ist in Gl. (3.9) definiert, η = 1 −(Tk/Tw).Im voliegenden Fall ergibt sichWir sehen, dass das Ergebnis im Wesentlichen mit dem Ergebnis aus Teilaufgabe (e) übereinstimmt. (Die Differenz ergibt sich daraus, dass in der vorausgegangenen Berechnung Werte mit weniger signifikanten Stellen eingesetzt wurden.)Wenn wir die Werte aus der Berechnung der übertragenen Wärmemenge in Teilaufgabe (e) in Gl. (3.6) einsetzen, erhalten wirDas Ergebnis ist null, wie für einen Carnot-Kreisprozess auch zu erwarten ist.

S3.1.5

1 (a) Wir betrachten einen Prozess, bei dem einer Kältequelle mit der Temperatur Tk die Wärmemenge dqk entnommen wird. Die Wärmemenge dqw wird bei der Temperatur Tw an die Wärmesenke abgegeben. Insgesamt beträgt die Entropieänderung eines derartigen ProzessesWir wollen zunächst annehmen, dass dqk = − dq und dqw = +dq ist, wobei dq positiv ist. Es folgtWegen Tw > Tk ist der Klammerterm negativ, und somit ist auch dS insgesamt negativ. Der hier beschriebene Prozess läuft also nicht freiwillig ab und ist daher aufgrund des Zweiten Hauptsatzes der Thermodynamik nicht erlaubt. Damit der Prozess ablaufen kann, muss also an der Maschine zusätzlich Arbeit verrichtet werden, damit |dqw| größer wird als |dqk| und somit schließlich auch dS positiv wird.

2 (b) Nun wollen wir annehmen, dass qk = −| q | undqw = | q | + | ω | ist. Die Gesamtänderung der Entropie ist in diesem FallDamit der Prozess nach dem Zweiten Hauptsatz der Thermodynamik erlaubt ist, muss die Clausius’sche Ungleichung (Gl. (3.12), dS ≥ 0) erfüllt sein. Es muss alsogelten, und somit ergibt sich für die erforderliche Arbeit

S3.1.7Wir wollen annehmen, dass sich zwei adiabatische Wege an einem Punkt A schneiden, wie es in Abb. 3.1gezeigt ist. Zwei weitere Punkte B und C, die jeweils derselben Temperatur wie auch Punkt A entsprechen, sollen in einiger Entfernung auf den Adiabaten liegen, so dass sich über iso therme Wege ein Kreisprozess ergibt.

Nun überlegen wir uns die Energieänderung für jeden der drei Schritte: Schritt 1 (A → B) stellt einen adiabatischen Weg dar, d. h. es findet keine Wärmeübertragung statt, q 1= 0. Die Änderung der Inneren Energie während Schritt 1 ist daher ∆ U 1= ω 1+ q 1= ω 1. Schritt 2 (B → C) stellt einen isothermen Weg dar; wenn wir davon ausgehen, dass die Energie des Systems ausschließlich eine Funktion der Temperatur ist (wie es z. B. für ein ideales Gas der Fall ist), gilt ∆ U 2= ω 2+ q 2= 0. Schritt 3 (C → A) stellt erneut einen adiabatischen Weg dar, d. h. es findet keine Wärmeübertragung statt, q 3= 0. Die Änderung der Inneren Energie während Schritt 3 ist daher ∆ U 3= ω 3 + q 3= ω 3. Da wir vorausgesetzt haben, dass die Energie des Systems ausschließlich eine Funktion der Temperatur ist, gilt U B= UC, und somit