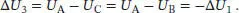
Demnach ist auch ω 1= − ω 3.
Da die Innere Energie eine Zustandsfunktion ist und es sich um einen geschlossenen Kreisprozess handelt, gilt:
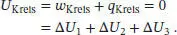
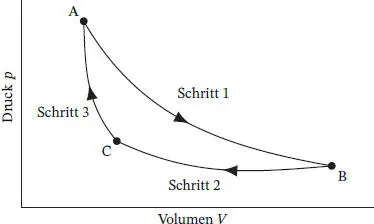
Abb. 3.1
Die insgesamt während des Kreisprozesses verrichtete Arbeit beträgt ω Kreis= ω 1 + ω 2+ ω 3 = ω 2, und die insgesamt aufgenommene Wärmemenge ist q Kreis = q 1 + q 2+ q 3 = q 2. Es wird deutlich, dass das alleinige Ergebnis des hier beschriebenen Kreisprozesses die Aufnahme der Wärmemenge q2 und deren Umwandlung in die Arbeit w 2ist. Dies steht in direktem Widerspruch zum Zweiten Hauptsatz der Thermodynamikin der Formulierung von Kelvin – es sei denn, es würde q 2 = ω 2 = 0 gelten, d. h. die Punkte B und C wären identisch und würden auf demselben Weg liegen. Als Ergebnis halten wir fest: Zwei reversible adiabatische Wege können sich niemals schneiden.
3.2 Entropieänderungen bei speziellen Prozessen
Diskussionsfrage
D3.2.1Die Regel von Pictet-Troutongilt deshalb, weil mit der Verdampfung beliebiger Flüssigkeiten jeweils vergleichbare Volumenänderungen verbunden sind; außerdem ist auch die damit verbundene Änderung der Anzahl möglicher Mikrozustände vergleichbar. Deshalb sollten die Standardverdampfungsentropien aller Flüssigkeiten ähnlich groß sein.
Einige Flüssigkeiten weichen jedoch signifikant von dieser Regel ab; die Ursache dafür ist, dass die Moleküle in diesen Fällen durch starke zwischenmolekulare Wechselwirkungen bis zu einem gewissen Grade assoziiert (also geordneter) vorliegen. Daher nimmt die Ordnung des Stoffs bei Verdampfung deutlicher ab.
Ein Beispiel ist flüssiges Wasser: Seine besondere Struktur, bedingt durch die Wasserstoffbrückenbindungen, spiegelt sich in einem relativ großen Wert der Verdampfungsenthalpie wider. Durch Wasserstoffbrücken bildet sich eine Organisation der Moleküle in Form einer Nahordnung heraus, die räumliche Verteilung der Moleküle ist weniger zufällig als bei Flüssigkeiten ohne Wasserstoffbrücken. Ähnliches gilt für Ethanol – bei diesem Alkohol bilden sich in der flüssigen Phase ebenfalls Wasser-stoffbrücken.
In Quecksilber existieren starke Wechselwirkungen zwischen den einzelnen Atomen; dies ist auch die Erklärung für die stark ausgeprägte Kohäsionskraft dieses Elements. Die Verdampfungsentropie von Quecksilber ist größer als durch die Regel von Pictet-Trouton vorhergesagt wird.
L3.2.1aDie Entropieänderung bei einem Phasenübergang ist durch Gl. (3.16) gegeben, ∆ Trans S = ∆ Trans H / T Trans. Wie in Abschn. 3.2.2 des Lehrbuchs erklärt wird, existieren in flüssigem Benzol keine Wasserstoffbrückenbindungen; daher lässt sich die Regel von Pictet-Trouton ohne Weiteres auf diese Substanz anwenden. Wir erhalten ∆ V S ⊖= +85 JK −1mol −1, und damit folgt für die (Standard-) Verdampfungsenthalpie
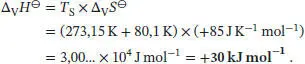
L3.2.2a
1 (i) Die Entropieänderung bei einem Phasenübergang ist durch Gl. (3.16) gegeben, ∆Trans S = ∆Trans H/TTrans. Für Trichlormethan (Chloroform) ergibt sich die (Standard-) Verdampfungsentropie
2 (ii) Da das System bei der Übergangstemperatur im Gleichgewicht vorliegt, gilt ∆Sges = 0 und folglich
L3.2.3aDie Temperaturabhängigkeit der Entropie ist durch Gl. (3.18) gegeben,
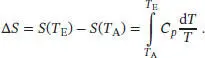
Wenn wir Cp im Temperaturbereich von T Abis T Eals konstant annehmen, vereinfacht sich diese Beziehung zu ∆ S = Cp ln( T E/ T A), wie in Abschn. 3.2.3 des Lehrbuchs erklärt wird. Der Anstieg der molaren Entropie von gasförmigem Sauerstoff im angegebenen Temperaturbereich ist damit
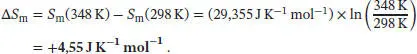
L3.2.4aWie in Abschn. 3.2.3 des Lehrbuchs erklärt wird, ist die Entropieänderung bei konstantem Volumen bei Variation der Temperatur durch
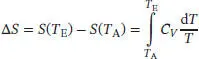
gegeben. Wir nehmen an, dass die (molare) Wärmekapazität von Neon im betrachteten Temperatur-bereich konstant und gleich 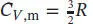 ist (wie bei einem idealen Gas). Für die molare Entropie bei 500 K erhalten wir
ist (wie bei einem idealen Gas). Für die molare Entropie bei 500 K erhalten wir
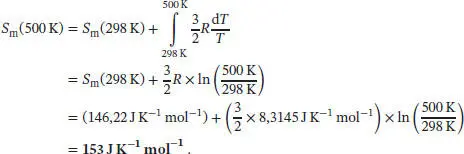
L3.2.5aDie beiden Metallblöcke werden durch den direkten Kontakt miteinander zunächst ins thermische Gleichgewicht kommen, d. h. ihre mittleren Temperaturen gleichen sich einander an und sind schließlich identisch. Die Endtemperatur ist

Obwohl dieses Resultat zunächst trivial erscheinen mag, so steckt doch weit mehr dahinter: Die Wärmekapazität bei konstantem Volumen ist in Gl. (2.14) definiert, CV = ( ∂ U /( ∂ T ) V. In Abschn. 2.1.4b des Lehrbuchs wird gezeigt, dass die Innere Energie bei konstanter Wärmekapazität linear mit der Temperatur ansteigt. Es gilt also ∆ U = C V∆ T = ∆ CV ( T E− T A). Die beiden Metallblöcke besitzen zunächst eine Anfangstemperatur von T 1bzw. T 2. Um die Endtemperatur T Ezu erreichen, ändert sich ihre jeweilige Innere Energie um ∆ U 1= CV ,1( T E– T A) bzw. ∆ U 2= CV, 1(T E- T 2). Die beiden Blöcke sind in unserem Beispiel gleich groß, und sie bestehen aus demselben Material, daher gilt CV ,1= CV ,2= CV . Da es sich um ein abgeschlossenes (isoliertes) System handelt, muss die Gesamtänderung der Inneren Energie ∆ U = ∆ U 1+ ∆ U 2= 0 betragen. Dies bedeutet, dass ∆ U = C V(( T E− T 1) − ( T E− T 2)) =C V ×(2 T E− ( T 1+ T 2)) = 0 gelten muss; die Endtemperatur ist daher 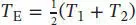 , wie bereits erwähnt.
, wie bereits erwähnt.
Читать дальше

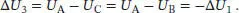
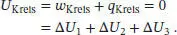

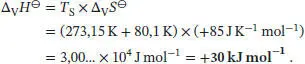
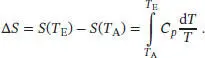
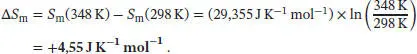
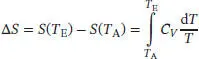
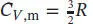 ist (wie bei einem idealen Gas). Für die molare Entropie bei 500 K erhalten wir
ist (wie bei einem idealen Gas). Für die molare Entropie bei 500 K erhalten wir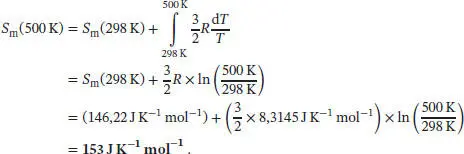

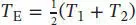 , wie bereits erwähnt.
, wie bereits erwähnt.










