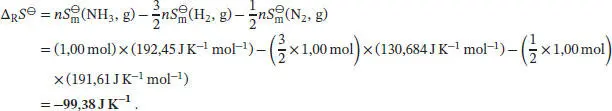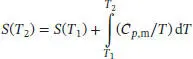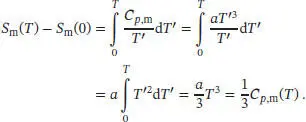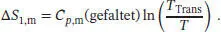
Als Nächstes betrachten wir die Entfaltung des Proteins. Diesen Schritt 2 wollen wir als Phasenübergang auffassen. Die Entropieänderung bei einem Phasenübergang ist durch Gl. (3.16) gegeben, ∆ Trans S = ∆ Trans H / T Trans, und somit gilt
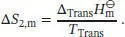
Im letzten Schritt 3 wird das nun entfaltete Protein wieder auf die ursprüngliche Temperatur abgekühlt, und es gilt
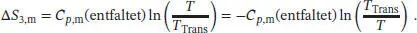
Die Gesamtänderung der molaren Entropie ergibt sich aus der Summe der Entropieänderungen dieser drei Schritte,
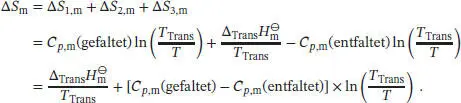
Mit der gegebenen Differenz der Wärmekapazitäten C p,m(entfaltet) − Cp ,m(gefaltet) = 6,28 × 10 3J K −1mol −1erhalten wir für die Entropie der Entfaltung von Lysozym bei 25 °C:
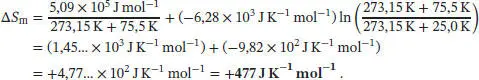
S3.2.11
1 (a) Wir betrachten einen Prozess, bei dem einer Kältequelle mit der Temperatur Tk die Wärmemenge |dq | entzogen und die Wärmemenge qw = |dq | + |dω | an eine Wärmesenke mit der Temperatur Tw abgegeben wird. Die Gesamtänderung der Entropie für diesen Vorgang istDamit der Prozess nach dem Zweiten Hauptsatz der Thermodynamik erlaubt ist, muss die Clau-sius’sche Ungleichung (Gl. (3.12), dS ≥ 0) erfüllt sein. Es muss alsogelten. Die mindestens notwendige Arbeit, damit diese Ungleichung erfüllt ist, ist diejenige, bei der die Beträge der beiden Terme auf der linken Seite identisch sind. Es folgt also, wie zu beweisen war,
2 (b) Um den Betrag der verrichteten Arbeit | dω | zu finden, stellen wir den Ausdruck aus Teilaufgabe (a) geeignet um, und mithilfe der Beziehung dq = C dTk erhalten wirDurch Integration auf beiden Seiten zwischen den in der Aufgabenstellung genannten Integrationsgrenzen erhalten wirDie Lösung dieses Integrals ist
3 (c) Mithilfe der Beziehung C = (m/M) Cp,m erhalten wir für die benötigte Arbeit
4 (d) Wenn wir voraussetzen, dass die Temperatur konstant gehalten wird, vereinfacht sich die in Teilaufgabe (a) hergeleitete Beziehung zuNach Umstellen erhalten wir für die benötigte ArbeitBeachten Sie, dass der Vorgang des Erstarrens bzw. Gefrierens lediglich die Umkehrung eines Schmelzvorgangs ist, daher gilt für die übertragene Wärmemenge q = ∆Trans H = (m/M) (−∆Sm H ⊖). Die benötigte Arbeit ist daher
5 (e) Die insgesamt benötigte Arbeit ergibt sich aus der Summe der beiden Beträge, die wir in den Teilaufgaben (c) und (d) berechnet haben, also ist
6 (f) Wenn wir unterstellen, dass es durch den Betrieb des Kühlgeräts nicht zu einem Energieverlust in Form einer Wärmeabgabe kommt, ergibt sich die Leistung aus der insgesamt verrichteten Arbeit pro Zeitintervall, also ist P = ωges/∆t. Somit ist das gesuchte Zeitintervall
3.3 Die Messung der Entropie
Diskussionsfrage
D3.3.1Da sich eine Lösung von Kationen nicht ohne die Anwesenheit von Anionen herstellen lässt (und umgekehrt), werden die (molaren) Standardentropien von Ionen in Lösung auf einer besonderen Skala angegeben, bei der – per Konvention – die Standardentropie von H +-Ionen in Wasser bei allen Temperaturen als Nullpunkt definiert ist: S ⊖(H +, aq) = 0.
Die Entropien von Ionen in wässriger Lösung werden relativ zu diesem Nullwert des H +-Ions angegeben; diese Werte können positiv oder negativ sein. Ein positiver Wert für die Entropie bedeutet, dass das betreffende Ion in wässriger Lösung eine größere molare Entropie besitzt als H +, und für eine negative Entropie ist das Gegenteil der Fall. Ein Ion mit einer Entropie von null besitzt logischerweise in wässriger Lösung die gleiche Entropie wie H +.
L3.3.1aWenn wir davon ausgehen, dass das Debye’sche T 3-Gesetz angewendet werden kann, dann gilt für die molare Wärmekapazität bei konstantem Druck Cp , m= aT 3. Die Temperaturabhängigkeit der Entropie ist durch Gl. (3.20a) gegeben,
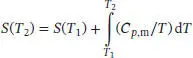
Für eine gegebene Temperatur T ist die Änderung der molaren Entropie, ausgehend vom absoluten Nullpunkt, daher
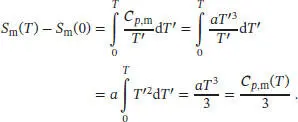
Im vorliegenden Fall erhalten wir für festes Silber bei 4,2 K
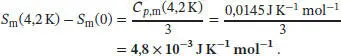
L3.3.2a
1 (i) Die Standardentropie der Reaktion 2 CH3CHO (g) + O2 (g) → 2 CH3COOH (l) ist
2 (ii) Die Standardentropie der Reaktion 2 AgCl (s) + Br2 (l) → 2 AgBr (s) + Cl2 (g) ist
3 (iii) Die Standardentropie der Reaktion Hg (l) + Cl2 (g) → HgCl2 (s) ist
L3.3.3aWir betrachten die chemische Reaktion
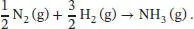
Die Standardreaktionsentropie ist durch Gl. (3.22b) gegeben, 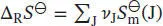 wobei v Jdie stöchiometrischen Faktoren sind. Mithilfe der Daten aus dem Anhang des Lehrbuchs finden wir für die Ammoniaksynthese aus den chemischen Elementen
wobei v Jdie stöchiometrischen Faktoren sind. Mithilfe der Daten aus dem Anhang des Lehrbuchs finden wir für die Ammoniaksynthese aus den chemischen Elementen
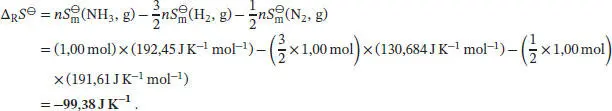
S3.3.1Wir betrachten die kalorimetrische Bestimmung der Entropie vom absoluten Nullpunkt bis hinauf zu der uns interessierenden Temperatur. Wenn wir davon ausgehen, dass das Debye’sche T 3-Gesetz angewendet werden kann, dann gilt für die molare Wärmekapazität bei konstantem Druck Cp , m= aT 3. Die Temperaturabhängigkeit der Entropie ist durch Gl. (3.20a) gegeben,
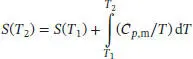
Für eine gegebene Temperatur T ist die Änderung der molaren Entropie, ausgehend vom absoluten Nullpunkt, daher
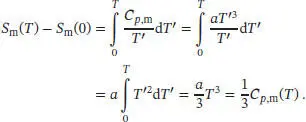
Im vorliegenden Fall erhalten wir für festes Quecksilber bei 10 K
Читать дальше

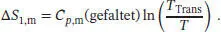
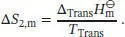
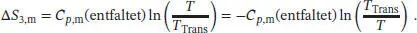
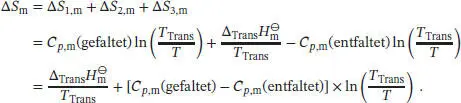
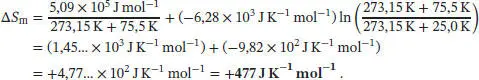
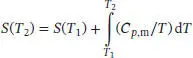
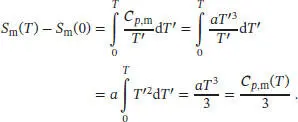
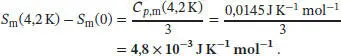
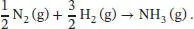
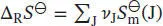 wobei v Jdie stöchiometrischen Faktoren sind. Mithilfe der Daten aus dem Anhang des Lehrbuchs finden wir für die Ammoniaksynthese aus den chemischen Elementen
wobei v Jdie stöchiometrischen Faktoren sind. Mithilfe der Daten aus dem Anhang des Lehrbuchs finden wir für die Ammoniaksynthese aus den chemischen Elementen