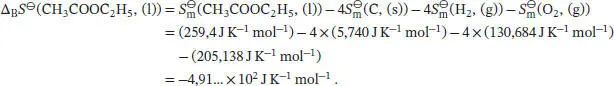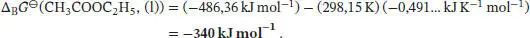L3.4.1aDie Freie Standardreaktionsenthalpie ist in Gl. (3.33) definiert, ∆ R G ⊖= ∆ R H ⊖- T ∆ R S ⊖. Die Standardreaktionsenthalpie ist durch Gl. (2.30b) gegeben, ∆ R H ⊖= ∑ J v J∆ B H ⊖(J), wobei v Jdie stöchiometrischen Faktoren sind. Bei Anwendung dieser Gleichung müssen wir die Vorzeichen von v Jbeachten (positiv für Produkte, negativ für Reaktanten).
1 (i) Die Standardenthalpie der Reaktion 2 CH3CHO (g) + O2 (g) → 2 CH3COOH (l) istDie Standardentropie dieser Reaktion haben wir bereits in Aufgabe L3.3.2a berechnet,Die Freie Standardreaktionsenthalpie ist
2 (ii) Die Standardenthalpie der Reaktion 2 AgCl (s) + Br2 (l) → 2AgBr (s) + Cl2 (g) istDie Standardentropie dieser Reaktion haben wir bereits in Aufgabe L3.3.2a berechnet,Die Freie Standardreaktionsenthalpie ist
3 (iii) Die Standardenthalpie der Reaktion Hg (l) + Cl2 (g) → HgCl2 (s) istDie Standardentropie dieser Reaktion haben wir bereits in Aufgabe L3.3.2a berechnet,Die Freie Standardreaktionsenthalpie ist
L3.4.2aDie Standardreaktionsentropie ist durch Gl. (3.22b) gegeben, 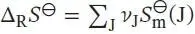 , wobei v Jdie stöchiometrischen Faktoren sind. Mit den Werten aus dem Anhang des Lehrbuchs erhalten wir
, wobei v Jdie stöchiometrischen Faktoren sind. Mit den Werten aus dem Anhang des Lehrbuchs erhalten wir
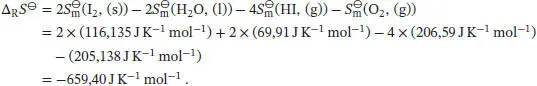
Die Standardreaktionsenthalpie ist durch Gl. (2.30b) gegeben, ∆ R H ⊖= ∑ J∆ B H ⊖(J). Unter Beachtung des Vorzeichens von v J(positiv für Produkte, negativ für Reaktanten) schreiben wir
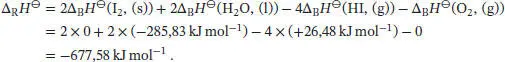
Die Freie Standardreaktionsenthalpie ist durch Gl. (3.33) gegeben, ∆ R G ⊖= ∆ R H ⊖− T∆ R S ⊖, und wir erhalten
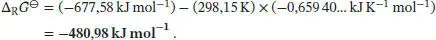
L3.4.3aDie Freie Standardreaktionsenthalpie ist durch Gl. (3.34b) gegeben, ∆ R G ⊖= ∑ J ν J∆ B G ⊖(J), wobei ν Jdie stöchiometrischen Faktoren sind. Für die Reaktion CH 4(g) + 2O 2(g) → CO 2(g) + 2H 2O (l) ist
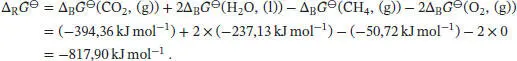
Wie in Abschn. 3.4.1e des Lehrbuchs erklärt wird, entspricht die maximale Nichtvolumenarbeit dem Betrag der Freien Reaktionsenthalpie. Die maximale Nichtvolumenarbeit ist daher | ω e,max| = |∆ R G ⊖| = 817, 90 kJ mol - 1.
L3.4.4aDie Freie Standardreaktionsenthalpie ist durch Gl. (3.34b) gegeben, ∆ R G ⊖= ∑ J ν J∆ B G ⊖(J), wobei ν Jdie stöchiometrischen Faktoren sind.
1 (i) Für die Reaktion 2 CH3CHO (g) + O2 (g) → 2 CH3COOH (l) erhalten wir
2 (ii) Für die Reaktion 2 AgCl (s) + Br2 (l) → 2 AgBr (s) + Cl2 (g) erhalten wir
3 (iii) Für die Reaktion Hg (l) + Cl2 (g) → HgCl2 (s) erhalten wir
L3.4.5aWir betrachten die Verbrennungsreaktion
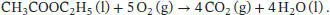
Die Standardreaktionsenthalpie ist durch Gl. (2.30b) gegeben, ∆ R H ⊖= ∑ J ν J∆ B H ⊖(J), wobei v Jdie stöchiometrischen Faktoren sind. Unter Beachtung des Vorzeichens von v J(positiv für Produkte, negativ für Reaktanten) schreiben wir
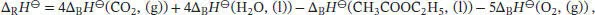
und durch Umstellen erhalten wir
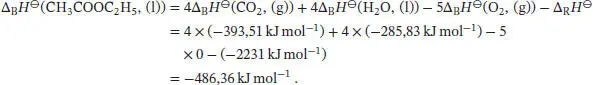
Die Standardreaktionsentropie ist durch Gl. (3.22b) gegeben, 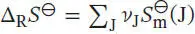 , wobei v Jdie stöchiometrischen Faktoren sind. Mithilfe der Daten aus dem Anhang des Lehrbuchs finden wir
, wobei v Jdie stöchiometrischen Faktoren sind. Mithilfe der Daten aus dem Anhang des Lehrbuchs finden wir
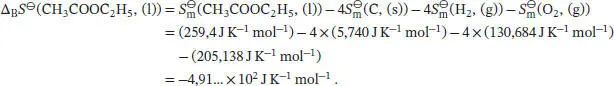
Die Freie Standardreaktionsenthalpie ist in Gl. (3.33) definiert, ∆ R G ⊖= ∆ R H ⊖ − T ∆ RS ⊖. Für die Verbindung Ethylacetat erhalten wir
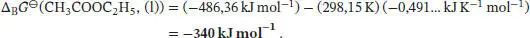
S3.4.1
1 (a) Mithilfe der Zustandsgleichung des idealen Gases ( Gl. (1.4), pV = nR T) finden wir für den EnddruckDas Endvolumen in Kammer A ist VA,E = (VA + VB) − VB,E = 3,00 dm3. Die Endtemperatur in Kammer A ist daher
2 (b) Wir berücksichtigen den Hinweis aus der Aufgabenstellung und betrachten zunächst die Erwärmung des Gases bei konstantem Volumen. Die Temperaturabhängigkeit der Entropie bei konstantem Volumen ist durch Gl. (3.19) gegeben, ∆S = nCV,mln(TE/TA), wobei hier Cp durch nCV ,m ausgetauscht wurde. Das Gas dehnt sich nun bis auf sein Endvolumen aus. Die Entropieänderung bei isothermer Expansion eines idealen Gases ist durch Gl. (3.14) gegeben, ∆S = nR ln(VE/VA). Für die Gesamtänderung der Entropie des Gases in Kammer A finden wir
3 (c) Die Temperatur von Kammer B wird während des gesamten Prozesses konstant gehalten, daher müssen wir in diesem Fall nur die Volumenänderung betrachten:
4 (d) Wenn wir annehmen, dass die Wärmekapazität im betrachteten Temperaturbereich konstant ist, wird die Änderung der Inneren Energie aufgrund einer Temperaturänderung durch Gl. (2.15b) wiedergegeben, ∆U = CV∆T. Da die Innere Energie eines idealen Gases ausschließlich von der Temperatur abhängig ist, erhalten wir
5 (e) Die Freie Energie (auch Helmholtz-Energie) ist in Gl. (3.28a) definiert als A = U − TS. Für endliche, messbare Änderungen können wir ∆A = ∆U − ∆(TS) = ∆U − T∆S − S∆T schreiben. Da die Temperatur von Kammer B konstant gehalten wird, ist ∆T = 0 und somitEs nicht möglich, den entsprechenden Ausdruck für Kammer A zu formulieren, da dort ∆T ≠ 0 und kein Wert für S angegeben ist.
6 (f) Wenn wir davon ausgehen, dass der Prozess reversibel verläuft, gilt für die Gesamtänderung der Freien Energie ∆A = ∆AA + ∆AB = 0. Dies würde bedeuten, dass ∆AA = −∆AB sein muss.
S3.4.3Wir betrachten den thermodynamischen Kreisprozess, der in Abb. 3.5gezeigt ist.
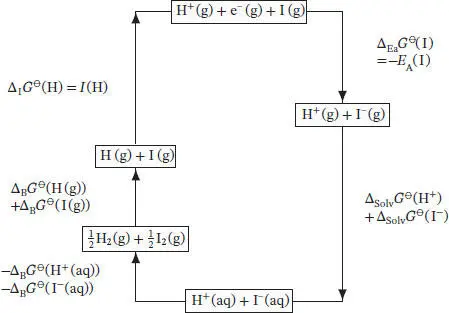
Abb. 3.5
Читать дальше

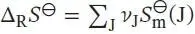 , wobei v Jdie stöchiometrischen Faktoren sind. Mit den Werten aus dem Anhang des Lehrbuchs erhalten wir
, wobei v Jdie stöchiometrischen Faktoren sind. Mit den Werten aus dem Anhang des Lehrbuchs erhalten wir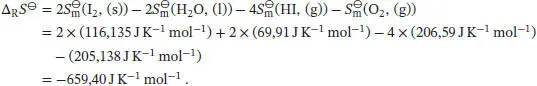
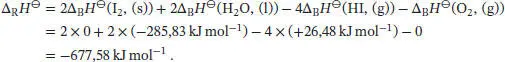
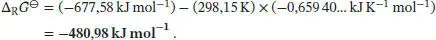
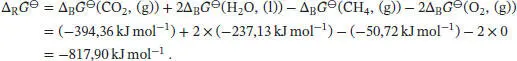
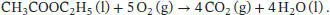
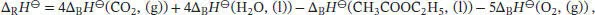
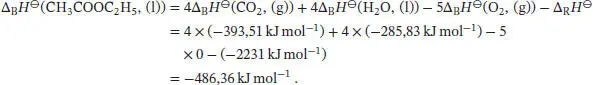
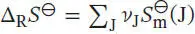 , wobei v Jdie stöchiometrischen Faktoren sind. Mithilfe der Daten aus dem Anhang des Lehrbuchs finden wir
, wobei v Jdie stöchiometrischen Faktoren sind. Mithilfe der Daten aus dem Anhang des Lehrbuchs finden wir