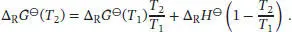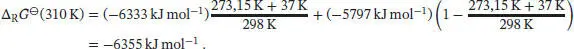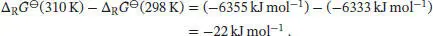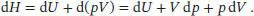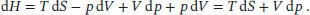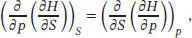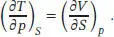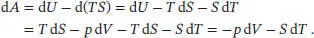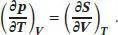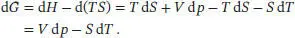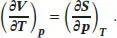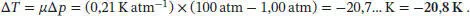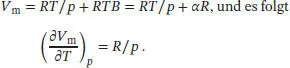James J. Keeler - Arbeitsbuch zu Atkins, de Paula, Keeler Physikalische Chemie

S3.5.3Durch Umstellen des Ausdrucks für die Änderung der Freien Enthalpie aus Aufgabe S3.5.1 nach ∆ G ( T 2) erhalten wir

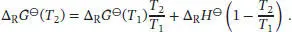
Bei 37°C = 310 K erhalten wir

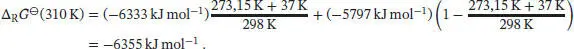
Die zusätzliche Nichtvolumenarbeit, die durch diese Temperaturerhöhung gewonnen werden kann, ergibt sich aus der Differenz

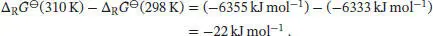
Wir sehen, dass zusätzliche 22 kJ mol−1an Nichtvolumenarbeit bei der höheren Temperatur verrichtet werden kann.

S3.5.5Wir betrachten das totale Differenzial der Enthalpie, H = U + pV,

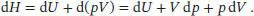
Das totale Differenzial der Inneren Energie ergibt sich aus der Fundamentalgleichung, d U = T d S - p d V (Gl. (3.37)), und wir schreiben

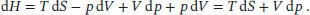
Da es sich bei d H um ein totales Differenzial handelt, schreiben wir

Für partielle Ableitungen gilt allgemein, dass die Reihenfolge sukzessiver Ableitungen für das Ergebnis unerheblich ist (siehe „Toolkit 10: Totale Differenziale“ in Abschn. 3.5.1 des Lehrbuchs),

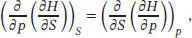
und somit gilt

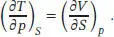
Nun betrachten wir in analoger Weise die totalen Differenziale der Freien Energie (auch Helmholtz- Energie), A = U − TS, und der Freien Enthalpie (auch Gibbs-Energie), G = H − TS. Wir beginnen mit der Freien Energie,

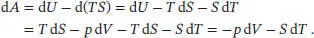
Daraus folgt

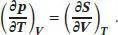
Bei der Betrachtung des totalen Differenzials der Freien Enthalpie berücksichtigen wir das Ergebnis für d H, und wir schreiben

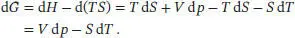
Daraus folgt

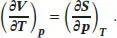
S3.5.7

1 (a) Wir nehmen zunächst an, dass nur die abstoßenden Wechselwirkungen signifikant sind, d. h. es gilt a = 0 und b ≠ 0 . Damit vereinfacht sich die Van-der-Waals-Gleichung (Gl. (1.27b)) zu p = RT /(Vm − b). Für das molare Volumen Vm schreiben wir daherNun betrachten wir das totale Differenzial der molaren Freien Enthalpie bei konstanter Temperatur, dGm = (∂Gm /∂p)T dp. Integration dieser Beziehung liefertund somit giltWir erkennen: Die druckabhängige Änderung der Freien Enthalpie ist für ein Van-der-Waals-Gas stärker ausgeprägt als für ein ideales Gas; der Grund hierfür ist im letzten Term des soeben erhaltenen Ausdrucks zu suchen, der die abstoßenden Wechselwirkungen zwischen den Gasmolekülen berücksichtigt.

2 (b) Nun nehmen wir an, dass nur die anziehenden Wechselwirkungen signifikant sind, d. h. es gilt a ≠ 0 undb = 0. Damit vereinfacht sich die Van-der-Waals-Gleichung (Gl. (1.27b)) Für das molare Volumen Vm schreiben wir daherDie möglichen Lösungen dieser quadratischen Gleichung in Vm sindDa die Van-der-Waals-Gleichung eine Art „Korrektur“ der Zustandsgleichung des idealen Gases darstellt, sollte die physikalisch sinnvolle Lösung ein ähnliches Ergebnis liefern. Wegen 4 pa/(RT)2 ≪1 stellt sich heraus, dass wir nur bei Berücksichtigung des positiven Vorzeichens vor der Wurzel ein Ergebnis erhalten, das diesen Umstand wiedergibt und damit physikalisch sinnvoll ist. Auf dieses Ergebnis wenden wir nun die in der Aufgabenstellung vorgeschlagene Reihenentwicklung an,Durch Integration erhalten wir für die Druckabhängigkeit der Freien Enthalpieund somit giltWir erkennen: Die druckabhängige Änderung der Freien Enthalpie ist für ein Van-der-Waals-Gas stärker ausgeprägt als für ein ideales Gas; der Grund hierfür ist im letzten Term des soeben erhaltenen Ausdrucks zu suchen, der die abstoßenden Wechselwirkungen zwischen den Gasmolekülen berücksichtigt. Abb. 3.6 Abb. 3.7

3 (c) Eine Auftragung der Änderung der molaren Freien Enthalpie, ∆Gm(p) = Gm(p) − Gm(p⊖), gegen p/p⊖ = 25 mit den gegebenen Daten ist in Abb. 3.6gezeigt. In Abb. 3.7ist eine vergrößerte Darstellung des Bereichs zwischen p/p⊖ = 25 und p/p⊖ = 50 separat gezeigt.

A3.1Der Joule-Thomson-Koeffizient ist in Gl. (2.46) definiert, μ = (∂T/∂p)H . Bei einer Joule-Thomson-Expansion (siehe Abschn. 2.4 des Lehrbuchs) ist die Enthalpie konstant, daher ergibt sich für die Temperaturänderung

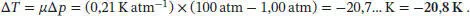
Nach der Expansion ist die Temperatur des Gases daher 373 − 20,7. = 3,52… × 10 2K.

Zur Berechnung der Entropieänderung teilen wir die Expansion gedanklich auf in einen ersten Schritt, der bei konstanter Temperatur stattfindet, und einen zweiten Schritt, in dem das Gas bei konstantem Druck abgekühlt wird. Die Entropieänderung für den ersten Schritt ist durch Gl. (3.19) gegeben,

Zur Berechnung der Entropieänderung des zweiten Schritts verwenden wir die passende Maxwell- Beziehung aus Tab. 3.5 des Lehrbuchs, (∂ S /∂ p ) T= - ( ∂V/∂T)P. Im vorliegenden Fall gilt pV m= RT (1 + Bp ), und der temperaturabhängige Virialkoeffizient besitzt die Form B = α/T. Daher gilt

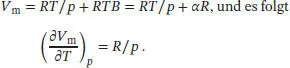
Dies entspricht dem Ergebnis für ein ideales Gas. Die Integration von (∂S m /∂p)T = -R/p liefert daher