James J. Keeler - Arbeitsbuch zu Atkins, de Paula, Keeler Physikalische Chemie

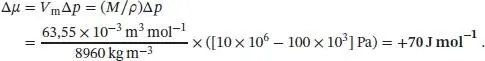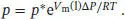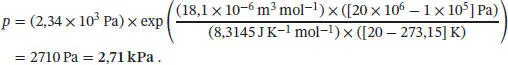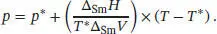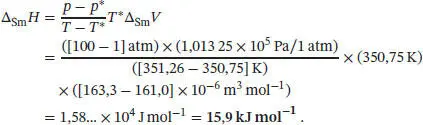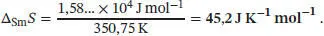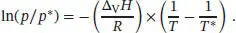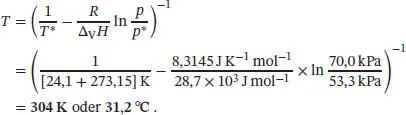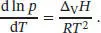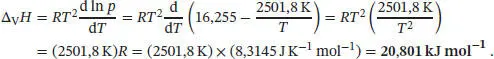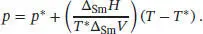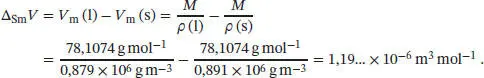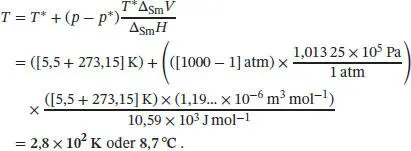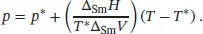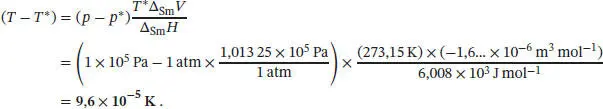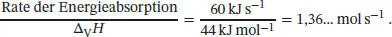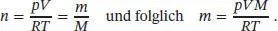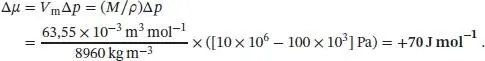
Dabei haben wir 1 Pa m 3= 1 J verwendet. Außerdem haben wir angenommen, dass die Probe inkompressibel ist.

L4.2.4aDer Effekt eines ausgeübten Drucks Δ p auf den Dampfdruck einer Flüssigkeit ist durch Gl. (4.4) gegeben,

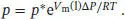
Für den Dampfdruck von Wasser unter den gegebenen Bedingungen erhalten wir

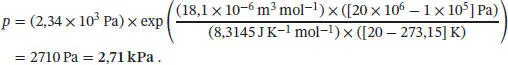
L4.2.5aDie Beziehung zwischen dem Druck und der Temperatur entlang der Phasengrenzlinie fest/flüssig ist durch Gl. (4.9) gegeben,

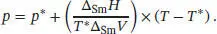
Diesen Ausdruck stellen wir nach Δ Sm H um und setzen die gegebenen Werte ein, p * = 1,00 atm, T * = 350,75 K, p = 100 atm und T = 351,26 K. Wir erhalten für die Schmelzenthalpie

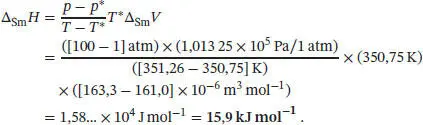
Die Entropieänderung bei einem Phasenübergang ist durch Gl. (3.16) gegeben, Δ Trans S = Δ Trans H / T Trans, wobei T Transdie Übergangstemperatur ist. Am Schmelzpunkt erhalten wir damit für die Schmelzentropie des beschriebenen Festkörpers

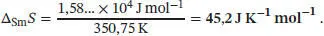
L4.2.6aDie integrierte Form der Clausius-Clapeyron-Gleichung (Gl. (4.12)) lautet

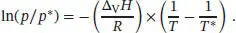
Wir nehmen an, dass der Dampf sich ideal verhält; außerdem soll die Verdampfungsenthalpie Δ V H nicht von der Temperatur abhängen. Nach Umstellen des obigen Ausdrucks nach T können wir schreiben:

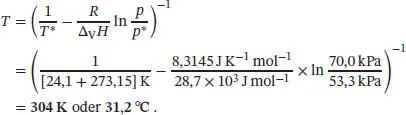
L4.2.7aDie Clausius-Clapeyron-Gleichung (Gl. (4.11)) lautet

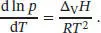
Wir stellen nach Δ V H um und differenzieren den Ausdruck für ln p. Es spielt keine Rolle, dass der Druck hier in der Einheit Torr angegeben ist, denn wir benötigen lediglich die (dimensionslose) Steigung von ln p. Somit erhalten wir für die Verdampfungsenthalpie der Flüssigkeit

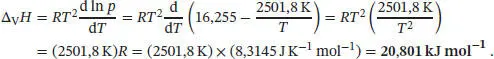
L4.2.8a

1 (i) Die Clausius-Clapeyron-Gleichung (Gl. (4.11)) lautetWir stellen nach ΔVH um und differenzieren den Ausdruck für ln p; dabei müssen wir beachten, dass ln x = (ln 10) log x ist. Es spielt keine Rolle, dass der Druck hier in der Einheit Torr angegeben ist, denn wir benötigen lediglich die (dimensionslose) Steigung von ln p. Somit erhalten wir für die Verdampfungsenthalpie von Benzol

2 (ii) Der Normalsiedepunkt entspricht derjenigen Temperatur, bei der der Dampfdruck 1 atm = 760 Torr beträgt. Wir stellen die in der Aufgabenstellung gegebene Formel log(p/Torr) = 7,960 − (1780 K)/T nach T um und setzen einen Druck von p = 760 Torr ein, und für den Normalsiedepunkt von Benzol ergibt sichBeachten Sie, dass diese Temperatur außerhalb des Bereichs von 10 °C bis 30 °C liegt, für den bekannt ist, dass die empirische Formel für log(p/Torr) aus der Aufgabenstellung gültig ist. Bei diesem Ergebnis handelt sich also lediglich um eine Näherung.

L4.2.9aDer Zusammenhang zwischen Druck und Temperatur entlang der Phasengrenzline fest/flüssig ist durch Gl. (4.9) gegeben,

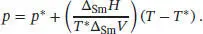
Die Größe Δ Sm V lässt sich mithilfe der Beziehung V m= M/ρ bestimmen, wobei M die Molmasse und ρ (rho) die Dichte der untersuchten Verbindung ist (in diesem Fall Benzol):

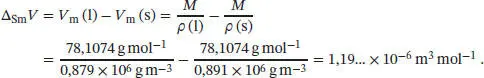
Durch Umstellen von Gl. (4.9) nach T erhalten wir für den Gefrierpunkt von Benzol bei dem gegebenen Druck

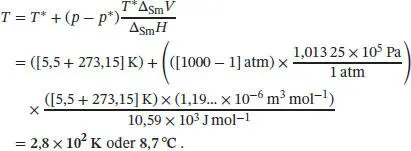
L4.2.10aDer Zusammenhang zwischen Druck und Temperatur entlang der Phasengrenzline fest/flüssig ist durch Gl. (4.9) gegeben,

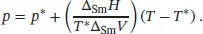
Die Normal- und die Standardübergangstemperaturen unterscheiden sich durch den Druck, bei dem der Phasenübergang stattfindet: „Normal-“ bezieht sich auf exakt p * = 1 atm (101 325 Pa), „Standard-“ dagegen auf exakt p = 1 bar (10 5Pa). Um die Differenz der beiden Varianten der Schmelzpunkte berechnen zu können, stellen wir Gl. (4.9) nach ( T − T *) um, und wir erhalten

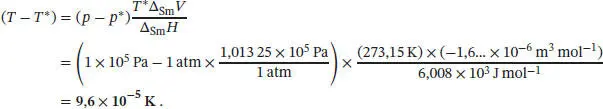
Dieses Ergebnis zeigt, dass die Standardschmelztemperatur geringfügig höher liegt als die Normalschmelztemperatur. In den meisten Fällen ist diese Differenz für praktische Zwecke jedoch vernachlässigbar klein.

L4.2.11aDie Geschwindigkeit der Verdunstung lässt sich mithilfe der zeitlichen Änderung der Wassermasse ausdrücken. Mit 1W = 1 J s −1ergibt sich für die absorbierte Energie (1,2 kW m −2) × (50 m 2) = 60 kJ s −1. Die Geschwindigkeit der Verdunstung beträgt damit

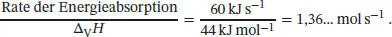
Durch Multiplikation mit der Molmasse von Wasser erhalten wir für den Wasserverlust durch Verdunstung (1,36…mol s −1) × (18,0158 g mol −1) = 25 g s −1.

L4.2.12aDas Volumen beträgt 75m 3; wir nehmen an, dass die Zustandsgleichung idealer Gase ( Gl. (1.4)) gilt,

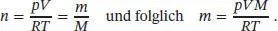
1 (i) Wasser: