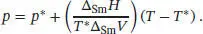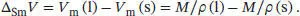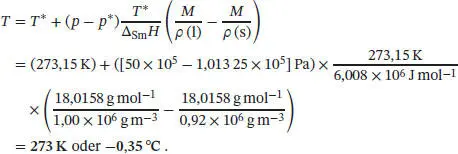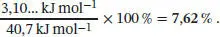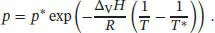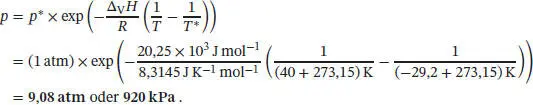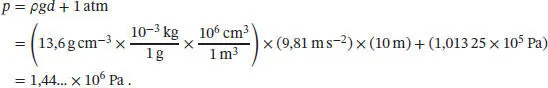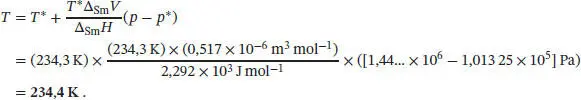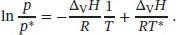2 (ii) Benzol:
3 (iii) Quecksilber:Dabei haben wir 1 Pa = 1 kg m−1 s−2 und 1 J = 1 kg m2 s−2 verwendet.
Anmerkung: Der Inhalt einer typischen Laborflasche mit Benzol (die deutlich weniger als 31 kg dieser Substanz enthalten dürfte) würde vollständig verdampfen, bevor die Luft des Labors mit Benzoldampf gesättigt wäre.
L4.2.13a
1 (i) Die integrierte Form der Clausius-Clapeyron-Gleichung (Gl. (4.12)) lautetDiese Gleichung stellen wir nach ΔVH um, und anschließend setzen wir die Werte für p* und T* bei 85,8 °C sowie p und T bei 119,3 °C ein. Damit erhalten wir für die Verdampfungsenthalpie von Naphthalin
2 (ii) Nun stellen wir die integrierte Form der Clausius-Clapeyron-Gleichung (Gl. (4.12)) nach T um. Der Normalsiedepunkt (bei p = 1 atm) entspricht einem Dampfdruck von 1,013 25 × 105 Pa. Mit dem Wert für ΔVH aus Teilaufgabe (a) sowie den Werten für p* und T* erhalten wir
3 (iii) Um die Verdampfungsentropie ΔVS von Naphthalin am Siedepunkt zu finden, verwenden wir Gl. (3.16):
L4.2.14aDer Zusammenhang zwischen Druck und Temperatur entlang der Phasengrenzline fest/flüssig ist durch Gl. (4.9) gegeben,
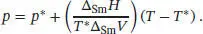
Die Größe Δ Sm V lässt sich mithilfe der Beziehung V m= M/ρ bestimmen, wobei M die Molmasse und ρ (rho) die Dichte der untersuchten Verbindung ist (in diesem Fall Wasser):
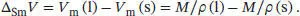
Diesen Ausdruck setzen wir in Gl. (4.9) ein, und anschließend stellen wir das Ergebnis nach T um. Für die Größen T*, p* und Δ V H verwenden wir die entsprechenden Werte am Normalschmelzpunkt von Eis, also 0 °C (273,15 K) und 1 atm (101,325 kPa). Außerdem gehen wir davon aus, dass Δ V H im betrachteten Temperaturbereich konstant ist. Wir erhalten
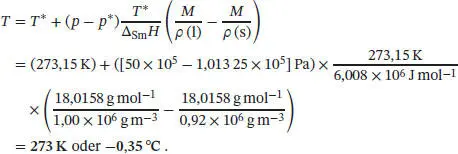
S4.2.1Die Volumenarbeit gegen einen konstanten äußeren Druck ist durch Gl. (2.6) gegeben, ω = − p exΔ V . Das molare Volumen eines Gases ist viel größer als das molare Volumen der gleichen Stoffmenge einer Flüssigkeit, daher ist Δ V V ≈ V m(g). Wenn wir außerdem davon ausgehen, dass sich das Gas ideal verhält, gilt gemäß der Zustandsgleichung idealer Gase ( Gl. (1.4)) V m= RT/p. Bei Expansion des Gases gegen einen äußeren Druck entspricht dieser dem Dampfdruck, also ist p = p ex. Die bei der Expansion verrichtete Volumenarbeit beträgt daher

Das negative Vorzeichen zeigt an, dass das System Arbeit an der Umgebung verrichtet, wodurch sich die Innere Energie des Systems verringert. Der Anteil der Verdampfungsenthalpie, der zur Expansion des Dampfs aufgewendet wird, ist
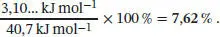
S4.2.3Die Variation des Dampfdrucks mit der Temperatur ist durch die integrierte Form der Clausius-Clapeyron-Gleichung (Gl. (4.12)) gegeben,
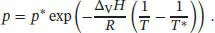
Mit den gegebenen Werten für T * und p * am Normalsiedepunkt erhalten wir
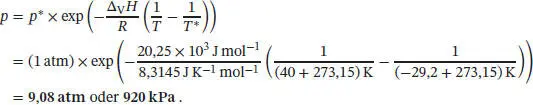
S4.2.5
1 (a) Die Variation des chemischen Potenzials mit der Temperatur (bei konstantem Druck) ist in Gl. (4.3a) gegeben, (∂μ/∂T)p = − Sm Wir erkennen: Die Steigung der Änderung des chemischen Potenzials mit der Temperatur entspricht dem Negativen der molaren Entropie. Die Differenz zwischen den Steigungen vor und nach Erreichen des Normalgefrierpunkts führt uns daher zur Schmelzenthalpie von Wasser (allerdings mit umgekehrtem Vorzeichen):
2 (b) Auf ähnliche Weise wie in Teilaufgabe (a) beschrieben führt uns die Differenz zwischen den Steigungen vor und nach Erreichen des Normalsiedepunkts zur Verdampfungsenthalpie von Wasser (allerdings mit umgekehrtem Vorzeichen):
3 (c) Wir rekapitulieren das Ergebnis von Teilaufgabe (a):Für eine endliche, messbare Änderung gilt Δ[μ(l) − μ(s)] = −ΔsmS × ΔT. Wenn die Temperatur um 5 °C sinkt, erhalten wirDa Wasser und Eis bei 0 °C im Gleichgewicht vorliegen, gilt am Schmelzpunkt μ(l) − μ(s) = 0. Daraus folgt, dass das chemische Potenzial von auf −5 °C unterkühltem, flüssigem Wasser das chemische Potenzial von Eis um +110 J mol−1 übersteigt. μ(l) > μ(s) ist, zeigt das unterkühlte Wasser ein starkes Bestreben, zu Eis zu gefrieren.
S4.2.7Der Gesamtdruck am Boden der Flüssigkeitssäule ist
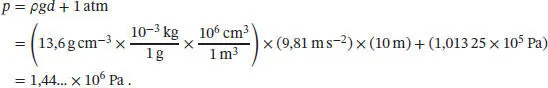
Der Gefrierpunkt lässt sich mithilfe von Gl. (4.9) bestimmen, p = p * + (Δ Sm H / T *Δ Sm V )( T − T *). Umstellen nach T und Einsetzen der gegebenen Werte liefert für Quecksilber
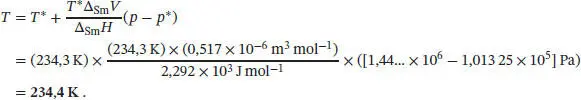
Beachten Sie, dass dieser Wert nur geringfügig (um 0,1 K) vom Normalschmelzpunkt der Verbindung abweicht. Dies ergibt sich daraus, dass die Steigung der Fest/Flüssig-Phasengrenze im Vergleich zur Steigung der Flüssig/Gas-Phasengrenze sehr viel größer ist. Aus diesem Grunde muss (z. B. in der technischen Chemie) bei sehr hohen Drücken gearbeitet werden, um den Gefrierpunkt einer Verbindung signifikant zu beeinflussen.
S4.2.9Wir stellen die integrierte Form der Clausius-Clapeyron-Gleichung (Gl. (4.12)) folgendermaßen um:
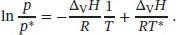
Bei Auftragung von ln( p/p *) gegen 1/T sollte sich eine Gerade mit der Steigung −Δ V H / R und dem Achsenabschnitt Δ V H / RT * ergeben; eine solche Auftragung ist in Abb. 4.2gezeigt. Wenn wir p * = 1 atm (oder 101,325 kPa) annehmen, entspricht T* dem Normalsiedepunkt, den wir aus dem Achsenabschnitt der Geraden bestimmen können.
| θ/°C |
p/kpa |
T−1/K−1 |
ln(p/p*) |
| 0 |
1,92 |
0,003 66 |
−3,966 |
| 20 |
6,38 |
0,003 41 |
−2765 |
| 40 |
17,70 |
0,003 19 |
−1745 |
| 50 |
27,70 |
0,003 09 |
−1297 |
| 70 |
62,30 |
0,002 91 |
−0,486 |
| 80 |
89,30 |
0,002 83 |
−0126 |
| 90 |
124.90 |
0,002 75 |
0,209 |
| 100 |
170,90 |
0,002 68 |
0,523 |
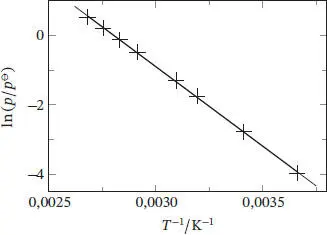
Abb. 4.2
Читать дальше