James J. Keeler - Arbeitsbuch zu Atkins, de Paula, Keeler Physikalische Chemie

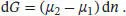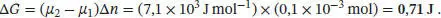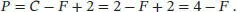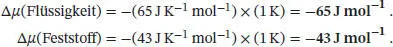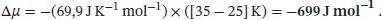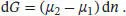
Arbeitsbuch zu Atkins, de Paula, Keeler Physikalische Chemie, 6. Auflage. Peter Bolgar, Haydn Lloyd, Aimee North, Vladimiras Oleinikovas, Stephanie Smith und James J. Keeler

© 2022 WILEY-VCH GmbH. Published 2022 by WILEY-VCH GmbH.

Wir wollen annehmen, dass 0,1 mmol eine hinreichend geringe Menge ist, sodass wir sie als „infinitesimal klein“ auffassen können. Im vorliegenden Fall ist folglich

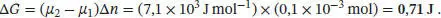
L4.1.3aWir verwenden die Phasenregel (Gl. (4.1), F = C − P + 2) mit C = 2 (für ein Zweikomponentensystem). Umstellen nach der Anzahl der Phasen P ergibt

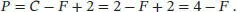
Die maximale Zahl von Phasen im Gleichgewicht tritt auf, wenn die Zahl der Freiheitsgrade F minimal ist (d. h. null); diese Zahl ist vier.

L4.1.4aWir verwenden die Phasenregel (Gl. (4.1), F = C − P + 2) mit C = 1 (für ein Einkomponentensystem). Einsetzen von P = 1 liefert F = 1 − 1 + 2 = 2. Die Bedingung P = 1 repräsentiert daher eine Fläche. Für eine Fläche ist F = 2, weil es möglich ist, zwei Variablen (den Druck und die Temperatur) innerhalb gewisser Grenzen unabhängig voneinander zu variieren. P = 1 zeigt an, dass nur eine einzige Phase vorliegt, was die Tatsache widerspiegelt, dass jede Fläche in einem Phasendiagramm eine Phase repräsentiert.

L4.1.5a

1 (i) Der Punkt für 200 K und 2,5 atm liegt auf der Grenze zwischen der festen und der Gasphase. Unter diesen Bedingungen würden also zwei Phasen vorliegen, die miteinander im Gleichgewicht stehen.

2 (ii) Der Punkt für 300 K und 4 atm liegt in der Gasphasenregion, daher liegt bei diesen Bedingungen nur eine Phase vor.

3 (iii) Die Temperatur 310 K überschreitet die kritische Temperatur von CO2, daher ist es in diesem Fall unmöglich, eine genaue Trennung zwischen der Gasphase und der flüssigen Phase vorzunehmen. Es liegt bei dieser Temperatur, unabhängig vom Druck, daher nur eine Phase vor (nämlich ein überkritisches Fluid, scCO2; siehe Abschn. 4.1.2a und „Anwendung 6: Technologie – Überkritische Fluide“ am Ende von Abschn. 4.1des Lehrbuchs).

S4.1.1

1 (a) Der Punkt für 100 K und 1 atm liegt in der Festkörperregion, daher liegt bei diesen Bedingungen ausschließlich festes Kohlendioxid (Trockeneis) vor. Wenn die Temperatur auf 194,7 K erhöht wird, ist der Sublimationspunkt von CO2 bei 1 atm erreicht; die feste Phase und die Gasphase liegen im Gleichgewicht vor. Oberhalb dieser Temperatur liegt ausschließlich gasförmiges Kohlendioxid, CO2 (g), vor.

2 (b) Der Punkt für 100 K und 70 atm liegt in der Festkörperregion, daher liegt auch bei diesen Bedingungen ausschließlich festes Kohlendioxid (Trockeneis) vor. Wenn die Temperatur erhöht wird, wird zunächst der Schmelɀpunkt der Verbindung erreicht; bei dieser Temperatur liegen die feste und die flüssige Phase im Gleichgewicht vor. Oberhalb dieser Temperatur liegt ausschließlich flüssiges Kohlendioxid, CO2 (l), vor, bis schließlich bei fortgesetztem Heizen der Siedepunkt der Verbindung erreicht wird; bei dieser Temperatur liegen die flüssige und die Gasphase im Gleichgewicht vor. Oberhalb dieser Temperatur liegt ausschließlich gasförmiges Kohlendioxid, CO2 (g), vor.

S4.1.3Ein schematisches Phasendiagramm des beschriebenen Einkomponentensystems ist in Abb. 4.1gezeigt. Beachten Sie, dass reale Phasengrenzen in aller Regel keine perfekt geraden Linien sind, sondern mehr oder weniger gekrümmte Kurven. Es existieren zwei Tripelpunkte, die in der Abbildung durch schwarze Kreise markiert sind.

Abb. 4.1

D4.2.1Die Variation des chemischen Potenzials mit der Temperatur (bei konstantem Druck) ist durch Gl. (4.3a) gegeben, ( ∂μ / ∂T ) p= − S m. Da die molare Entropie für alle reinen Substanzen stets eine positive Größe ist, ist die Steigung der Änderung des chemischen Potenzials aufgrund einer Temperaturänderung stets negativ. Das bedeutet: das chemische Potenzial nimmt bei einer Temperaturerhöhung grundsätzlich ab.

D4.2.3 Bei der dynamischen Differenzialkalorimetrie (DSC) wird die Wärmekapazität bei konstantem Druck ( Cp ) als Funktion der Temperatur gemessen, indem man die Probe elektrisch aufheizt und sie mit einer Referenz vergleicht (siehe Abschn. 2.3.4 des Lehrbuchs für eine ausführlichere Beschreibung der DSC). Phasenübergänge geben sich durch eine Diskontinuität bei Auftragung von Cp als Funktion der Temperatur zu erkennen. Die üblichen Phasenübergänge - wie beispielsweise Schmelzen oder Verdampfen - besitzen „latente“ Enthalpien, d. h. von null verschiedene Enthalpieänderungen bei konstanter Temperatur. Diese Übergänge verraten sich daher durch unendliche Werte von Cp an diesem Punkt. Bei Übergängen zweiter Ordnung ist Cp ebenfalls nicht stetig, wird aber nicht unendlich. Beide Varianten fallen in einem ansonsten stetigen Verlauf von Cp als Funktion der Temperatur sofort auf.

L4.2.1aDie Variation des chemischen Potenzials mit der Temperatur (bei konstantem Druck) ist durch Gl. (4.3a) gegeben, ( ∂μ / ∂T ) p= − S mFür eine endliche, messbare Änderung der Temperatur gilt Δ μ = − S mΔ T (vorausgesetzt, dass S mim betrachteten Temperaturbereich konstant ist). Somit gilt im vorliegenden Fall

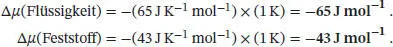
In beiden Fällen reduzieren sich die chemischen Potenziale aufgrund der Temperaturerhöhung; im Falle der Flüssigkeit ist diese Abnahme stärker ausgeprägt. Da die beiden Phasen (Wasser und Eis) am Normalschmelzpunkt im Gleichgewicht vorlagen, folgt: die Flüssigkeitist bei der neuen, erhöhten Temperatur die stabilere Phase. Aus diesem Grund läuft der Schmelzvorgang freiwillig ab.

L4.2.2aDie Variation des chemischen Potenzials mit der Temperatur (bei konstantem Druck) ist durch Gl. (4.3a) gegeben, ( ∂μ / ∂T ) p= − S mFür eine endliche, messbare Änderung der Temperatur gilt Δ μ = − S mΔ T (vorausgesetzt, dass S mim betrachteten Temperaturbereich konstant ist). Somit gilt im vorliegenden Fall

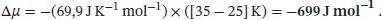
L4.2.3aDie Variation des chemischen Potenzials mit dem Druck (bei konstanter Temperatur) ist durch Gl. (4.3b) gegeben, ( ∂μ / ∂p ) T= V m. Für eine endliche, messbare Änderung der Temperatur gilt Δ μ = V mΔ p (vorausgesetzt, dass V mim betrachteten Temperaturbereich konstant ist). Das molare Volumen ist durch V m= M/ρ gegeben, wobei im vorliegenden Fall M die Molmasse von Kupfer und ρ (rho) die Dichte dieses Metalls ist. Somit gilt