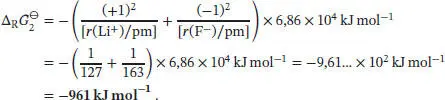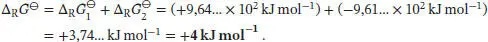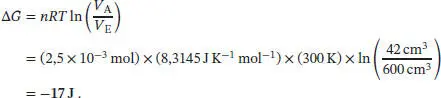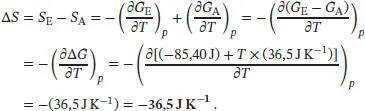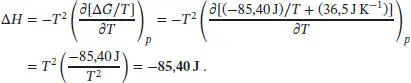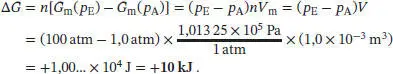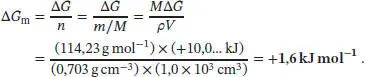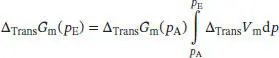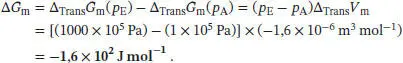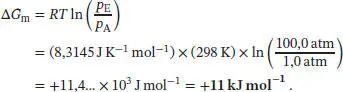Die Summe der Änderungen der Freien Enthalpien muss bei einem geschlossenen Kreisprozess gleich null sein. Daher schreiben wir
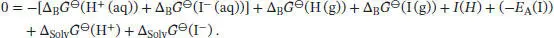
Da per Konvention ∆ B G ⊖(H +(aq) = 0 gilt, erhalten wir für die Freie Standardbildungsenthalpie von I −-Ionen in wässriger Lösung
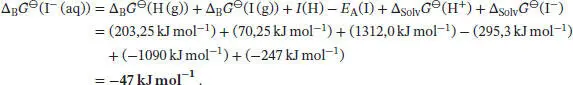
S3.4.5Die Freie Standardreaktionsenthalpie ist in Gl. (3.33) definiert, ∆ R G ⊖= ∆ R H ⊖− T ∆ R S ⊖. Die Standardreaktionsentropie ist durch Gl. (3.22b) gegeben, 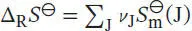 , wobei ν Jdie stöchiometrischen Faktoren sind. Daher schreiben wir
, wobei ν Jdie stöchiometrischen Faktoren sind. Daher schreiben wir
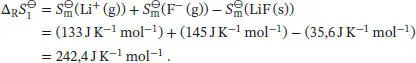
Somit ist die Freie Standardreaktionsenthalpie von Schritt 1
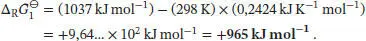
Für Schritt 2 gilt ∆ R G ⊖= ∆ Solv G ⊖(Li +) + ∆ Solv G ⊖(F −). Die Freie Enthalpie für das Lösen von Ionen in Wasser ist durch die folgende Variante der Born’schen Gleichung (Gl. (3.36b)) gegeben: 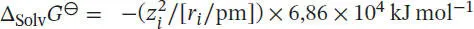 . Somit ist die Freie Standardreaktionsenthalpie von Schritt 2
. Somit ist die Freie Standardreaktionsenthalpie von Schritt 2
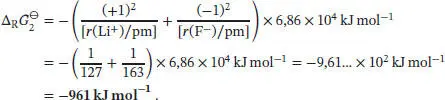
Die Freie Standardreaktionsenthalpie für den Gesamtprozess ist damit
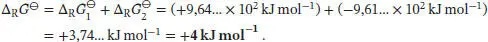
Wir sehen, dass das Vorzeichen dieser Größe positiv ist; der umgekehrte Prozess läuft also freiwillig ab.
3.5 Die Verbindung von Erstem und Zweitem Hauptsatz
Diskussionsfrage
D3.5.1Bei einem Temperaturanstieg führt die Beziehung (∂ G /(∂ T ) p= −S (Gl. (3.44)), kombiniert mit der Tatsache, dass die Entropie stets positiv ist, dazu, dass sich die Freie Enthalpie eines Systems (bei konstant gehaltenem Druck) grundsätzlich verringern muss.
L3.5.1aDie Abhängigkeit der (molaren) Freien Enthalpie eines idealen Gases vom Druck ist durch Gl. (3.50) gegeben, G m( p E) = G m( p A) + RT ln( p E/ p A). Aus der Zustandsgleichung des idealen Gases ( Gl. (1.4)) ergibt sich, dass der Druck umgekehrt proportional zum Volumen ist, p ∝ (1/ V ) (Boyle’sches Gesetz). Dies erlaubt es uns, Gl. (3.50) für eine isotherme Expansion so umzuformulieren, dass wir einen Ausdruck für die Änderung der Freien Enthalpie erhalten. Wir schreiben
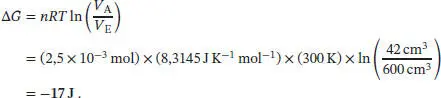
L3.5.2aDie Temperaturabhängigkeit der Freien Enthalpie bei konstantem Druck ist durch Gl. (3.44a) gegeben, (∂ G /∂ T ) p= − S . Die Entropieänderung ist daher
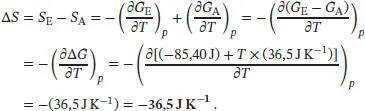
L3.5.3aDie Gibbs-Helmholtz-Gleichung für die Temperaturabhängigkeit der Freien Enthalpie (bei konstantem Druck) ist durch Gl. (3.47) gegeben, (∂[∆ G / T ]/∂ T ) P= −∆ H / T 2. Durch Umstellen dieser Beziehung erhalten wir für die Enthalpieänderung des in der Aufgabenstellung beschriebenen Prozesses
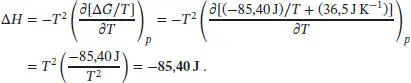
L3.5.4aDie Druckabhängigkeit der molaren Freien Enthalpie einer imkompressiblen Substanz ist durch Gl. (3.49) gegeben, G m( p E) = G m( p A) + ( p E− p A) V m. Wenn wir annehmen, dass das Volumen von Octan im betrachteten Druckbereich annähernd konstant bleibt, erhalten wir für die Änderung der Freien Enthalpie
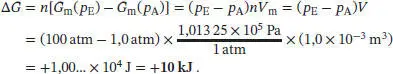
Für die Änderung der molaren Freien Enthalpie finden wir
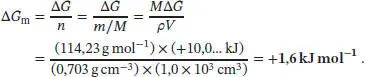
L3.5.5aIn Abschn. 3.5.2c des Lehrbuchs wird erklärt, dass die Druckabhängigkeit der Änderung der Freien Enthalpie bei einem Phasenübergang über
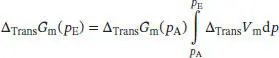
ausgedrückt werden kann. Wenn wir annehmen, dass ∆ Trans V mim betrachteten Druckbereich annähernd konstant bleibt, erhalten wir
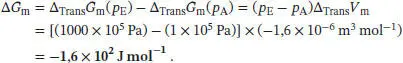
L3.5.6aDie Abhängigkeit der molaren Freien Enthalpie eines idealen Gases vom Druck ist durch Gl. (3.50) gegeben, G m( P E) = G m( P A) + RT ln( P E/ P A)- Wir erhalten
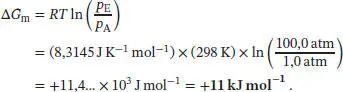
S3.5.1
1 (a) Die Gibbs-Helmholtz-Gleichung (Gl. (3.47)) beschreibt die Temperaturabhängigkeit der Freien Enthalpie bei konstantem Druck, (∂[∆G/T ]/∂ T)p = -∆H/T2. Integration dieser Gleichung zwischen T1 und T2 (unter der Annahme, dass ∆H in diesem Temperaturbereich konstant ist), liefertSomit gilt
2 (b) Die Freie Standardreaktionsenthalpie ist durch Gl. (3.34b) gegeben, ∆R G⊖ = ∑J νJ∆B G⊖(J), wobei νJ die stöchiometrischen Faktoren sind. Unter Beachtung des Vorzeichens von νJ (positiv für Produkte, negativ für Reaktanten) erhalten wirDie Standardreaktionsenthalpie ist durch Gl. (2.30b) gegeben, ∆R H⊖ = ∑J νJ∆B H⊖(J). Im vorliegenden Fall erhalten wir
3 (c) Durch Umstellen des Ausdrucks für die Änderung der Freien Enthalpie nach ∆G (T2) erhalten wirDamit ergibt sich bei der gegebenen Temperatur
Читать дальше

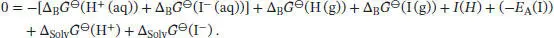
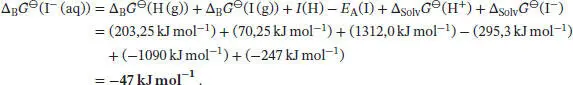
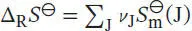 , wobei ν Jdie stöchiometrischen Faktoren sind. Daher schreiben wir
, wobei ν Jdie stöchiometrischen Faktoren sind. Daher schreiben wir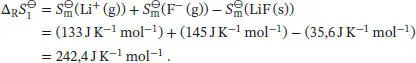
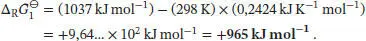
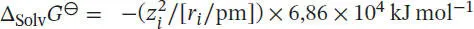 . Somit ist die Freie Standardreaktionsenthalpie von Schritt 2
. Somit ist die Freie Standardreaktionsenthalpie von Schritt 2