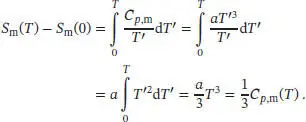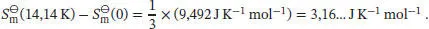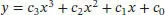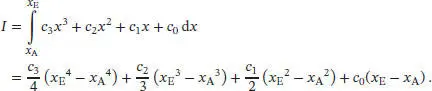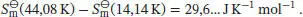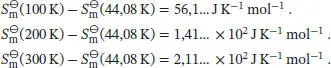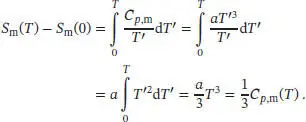
Im vorliegenden Fall erhalten wir
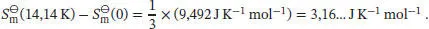
Die Entropieänderung wird bestimmt, indem wir die Fläche unter dem Graphen einer Auftragung von ( C p, m/ T ) gegen T untersuchen, wie sie in Abb. 3.3gezeigt ist.
| T/ K |
Cp,m/(J K−1 mol−1) |
(Cp,m/T)/(J K−2 mol−1) |
| 14,14 |
9,492 |
0,671 29 |
| 16,33 |
12,70 |
0,777 71 |
| 20,03 |
18,18 |
0,907 64 |
| 31,15 |
32,54 |
1,044 62 |
| 44,08 |
46,86 |
1,063 07 |
| 64,81 |
66,36 |
10,2392 |
| 100,90 |
95,05 |
0,942 02 |
| 140,86 |
121,3 |
0,861 14 |
| 183,59 |
144,4 |
0,786 54 |
| 225,10 |
163,7 |
0,727 23 |
| 262,99 |
180,2 |
0,685 20 |
| 298,06 |
196,4 |
0,658 93 |

Abb. 3.3
Wir erkennen, dass der Kurvenverlauf einigermaßen ungleichmäßig ist – eine recht gute Anpassung ist jedoch mithilfe von zwei Polynomfunktionen zweiten bzw. dritten Grades möglich, wobei die erste Funktion den Bereich von 14,14 K bis 44,08 K und die zweite den Bereich von 44,08 K bis 298,06 K abdeckt. Wenn wir y = ( CP ,m/ T )/(JK −2mol −1) und x = T /K definieren, lässt sich die angepasste Funktion über
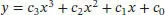
ausdrücken. Die Koeffizienten c i, mit denen die beste Anpassung der Funktion an den Kurvenverlauf in den beiden Temperaturbereichen zustande kommt, sind:
| ci |
14,14 K bis 44,08 K |
44,08 K bis 298,06 K |
| c 3 |
0 |
+7,1979 x 10 −9 |
| C 2 |
−7,6119 x 10 −4 |
−3,0830 x 10 −7 |
| C1 |
+5,6367 x 10 −2 |
−2,2415 x 10 −3 |
| C 0 |
−5,1090 x 10 −2 |
+1,1644 x 10 0 |
Das Integral der angepassten Funktionen im Bereich von x Abis x Elautet
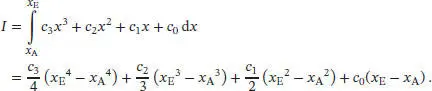
Uns interessiert der Temperaturbereich oberhalb von 44,08 K, daher beziehen wir den quadratischen Beitrag bei der Abschätzung der Entropie ein. Unter Verwendung der entsprechenden Koeffizienten und Integrationsgrenzen erhalten wir
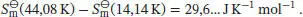
Die verbleibenden Beiträge finden wir, indem wir das Integral des kubischen Polynoms bis zur Temperaturgrenze 44,08 K betrachten. Für die andere Integrationsgrenze setzen wir 100 K, 200 K und (nach Extrapolation) 300 K ein, und wir erhalten:
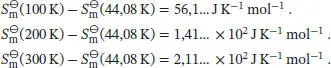
Die Standardentropien der Verbindung 1,3,5-Trichlor-2,4,6-trifluorbenzol nach dem Dritten Hauptsatz bei 100 K, 200 K und 300 K ergeben sich aus der Summe der berechneten Beiträge bis zu der jeweiligen Temperatur:

S3.3.9
1 (a) Auf Grundlage des gegebenen Ausdrucks für die molare Wärmekapazität bei konstantem Druck, Cp,m(T) = aT3 + bT, ergibt sich für Cp,m (T) /T:Dieser Ausdruck besitzt die allgemeine Form einer Geradengleichung, mit y = Steigung × x + Achsenabschnitt. Daraus folgt, dass die Steigung = a und der Achsenabschnitt = b ist.
2 (b) In Abb. 3.4ist eine Auftragung der gegebenen Daten gezeigt.T/KCp, m /(JK−1 mol−1)T2/(K2)(Cp, m/T)/(J K−2 mol−1)0,200,4370,0402,18500,250,5600,0632,24000,300,6930,0902,31000,350,8380,1232,39430,400,9960,1602,49000,451,1700,2032,60000,501,3610,2502,72200,551,5720,3032,8582Die Daten liegen in guter Näherung entlang einer Geraden; die Geradengleichung lautetSomit sind die gesuchten Werte der Konstanten a = 2, 569 J K−4 mol−1 und b = 2, 080 J K−2 mol−1.
3 (c) Die Temperaturabhängigkeit der Entropie ist durch Gl. (3.20a) gegeben,Für eine gegebene Temperatur T ist die Änderung der molaren Entropie, ausgehend vom absoluten Nullpunkt, daher Abb. 3.4
4 (d) Wenn wir davon ausgehen, dass der Ausdruck aus Teilaufgabe (c) auf eine Temperatur von 2,0 K extrapoliert werden kann, erhalten wir für die molare Entropie von Kalium bei dieser Temperatur
3.4 Die Beschränkung auf das System
Diskussionsfrage
D3.4.1Alle diese Ausdrücke ergeben sich aus einer Kombination des Ersten Hauptsatzes der Thermodynamik mit der Clausius’schen Ungleichung in der Form d S ≥ d q /T.
Sofern ein Prozess bei konstantem Volumen abläuft, wird logischerweise keine Volumenarbeit geleistet. Aus dem Ersten Hauptsatz folgt d U = d q . Wenn wir die Clausius’sche Ungleichung in die Form d S − d q / T ≥ 0 umstellen, folgt daraus d S − d U / T ≥ 0 und somit T d S ≥ d U .
Die Freie Energie (auch Helmholtz-Energie) ist in Gl. (3.28a) definiert als A = U − TS . Für eine Zustandsänderung bei konstanter Temperatur folgt d A = d U − T d S . Wir haben bereits gesehen, dass bei konstantem Volumen T d S ≥ d U gilt; somit muss d A ≤ 0 sein. Dies ist das Kriterium für die Freiwilligkeit eines Prozesses, der bei konstantem Volumen und konstanter Temperatur abläuft.
Als Nächstes betrachten wir einen Prozess, der bei konstantem Druck abläuft. Unter diesen Bedingungen entspricht die Wärmemenge der Enthalpieänderung, d. h. es gilt d H = d q . Mit einer ähnlichen Argumentation wie zuvor ergibt sich T d S ≥ d H .
Die Freie Enthalpie (auch Gibbs-Energie) ist definiert als G = H − TS . Für eine Zustandsänderung bei konstanter Temperatur folgt d G = d H - T d S . Wir haben bereits gesehen, dass bei konstantem Druck T d S ≥ d H gilt; somit muss d G ≤ 0 sein. Dies ist das Kriterium für die Freiwilligkeit eines Prozesses, der bei konstantem Druck und konstanter Temperatur abläuft.
Hinweis: In allen Fällen gibt das Ungleichheitszeichen die Bedingungen für spontane Änderungen an; das Gleichheitszeichen gilt jeweils für den Gleichgewichtsfall unter den genannten Bedingungen.
Читать дальше