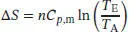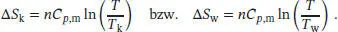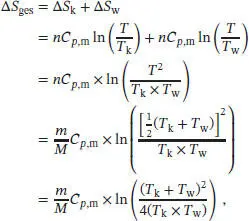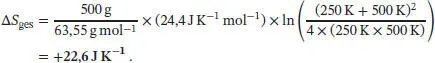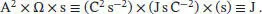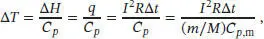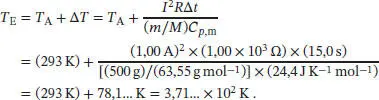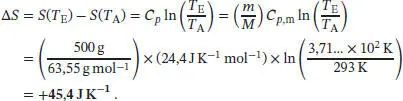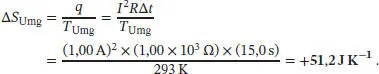2 (b) Um die Entropieänderung beim Verdampfen der Flüssigkeit bei der Temperatur T2 zu berechnen, verwenden wir einen ähnlichen Ansatz wie zuvor in Teilaufgabe (a). Wir stellen uns vor, dass wir die Flüssigkeit zunächst bis zu ihrer Siedetemperatur TS erhitzen, anschließend findet der Phasenübergang statt, und schließlich kühlen wir das entstandene Gas auf die Temperatur T2 ab. Für die Entropieänderungen erhalten wir (in analoger Weise wie in Teilaufgabe (a)):Die Gesamtänderung der Entropie ist daherWir sehen, dass dieser Betrag negativ ist (∆Sges < 0), d. h. gemäß dem Zweiten Hauptsatz der Thermodynamik verläuft dieser Prozess nicht freiwillig. Der umgekehrte Übergang g → l verläuft hingegen bei 95 °C spontan.
S3.2.3Wir stellen uns vor, dass wir Trichlormethan (Chloroform, CHCl 3) bei konstantem Druck von der gegebenen Anfangs- zur Endtemperatur erhitzen. Die Variation der Entropie mit der Temperatur bei konstantem Druck ist durch Gl. (3.18) gegeben,
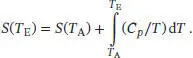
Für die molare Wärmekapazität bei konstantem Druck wird eine Abhängigkeit der Form Cp , m= a + bT vorausgesetzt, mit a = +91,47JK −1mol −1und b = +7,5 X 10 −2JK −2mol −1. Die Änderung der molaren Entropie, ∆ S m = S m( T E) − S m( T A), für diesen Prozess ist daher
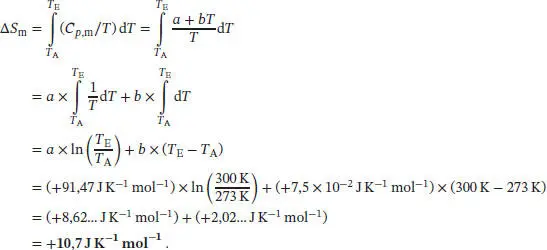
S3.2.5Die beiden Metallblöcke werden durch den direkten Kontakt miteinander zunächst ins thermische Gleichgewicht kommen, d. h. ihre mittleren Temperaturen gleichen sich einander an, und schließlich wird die Temperatur
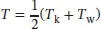
erreicht. Obwohl dieses Resultat zunächst trivial erscheinen mag, so steckt doch weit mehr dahinter: Die Wärmekapazität bei konstantem Volumen ist in Gl. (2.14) definiert, CV = ( ∂ U/∂ T)V . In Abschn. 2.1.4b des Lehrbuchs wird gezeigt, dass die Innere Energie bei konstanter Wärmekapazität linear mit der Temperatur ansteigt. Es gilt also ∆ U = CV ∆ T = CV(T E − T A). Die beiden Metallblöcke besitzen zunächst eine Anfangstemperatur von T kbzw. T w. Um die Endtemperatur T zu erreichen, ändert sich ihre jeweilige Innere Energie um ∆ U k= CV , k( T - T k) bzw. ∆ Uw = CV , w( T - T w). Die beiden Blöcke sind in unserem Beispiel gleich groß, und sie bestehen aus demselben Material, daher gilt CV, k = CV ,w = CV . Beachten Sie, dass sich die Innere Energie eines Festkörpers bei Variation des Volumens oder des Drucks nicht signifikant verändert, daher können wir CV = Cp = C voraussetzen. Da es sich um ein abgeschlossenes (isoliertes) System handelt, muss die Gesamtänderung der Inneren Energie ∆ U = ∆ U k+ ∆ U w= 0 betragen. Dies bedeutet, dass ∆ U = Cp (( T − T k) − ( T − T w)) = Cp × (2 T − ( T k+ T w)) = 0 gelten muss; die Endtemperatur ist daher 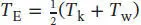 , wie bereits erwähnt.
, wie bereits erwähnt.
Die Temperaturabhängigkeit der Entropie bei konstantem Volumen ist durch Gl. (3.19) gegeben,
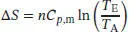
Für die beiden Metallblöcke gilt daher
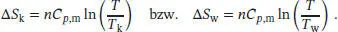
Die Gesamtänderung der Entropie des Systems ist
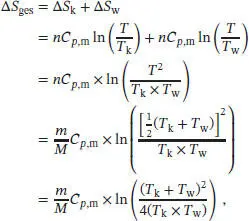
wobei m die Masse und M die Molmasse von Kupfer ist.
Durch Einsetzen der gegebenen Werte erhalten wir für den vorliegenden Fall
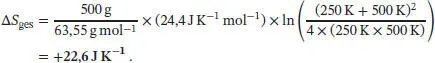
S3.2.7Die Wärmemenge, die durch den elektrischen Heizwiderstand im Zeitintervall ∆ t abgegeben wird, beträgt q = Leistung ×∆ t = IV ∆ t = I2R ∆ t. (Bei der letzten Umformung haben wir auf das Ohm’sche Gesetz zurückgegriffen, V = IR.) Zur Umrechnung der elektrischen in thermodynamische Einheiten verwenden wir (1A) = (1Cs −1) und (1V) = (1JC −1), es ergibt sich (1 Ω) = (1JsC −2). Die Einheiten für den finalen Ausdruck für die Wärmemenge sind wie erwartet
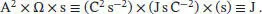
Wir nehmen an, dass die gesamte freigesetzte Wärme bei konstantem Druck vom Metallblock aufgenommen wird. Die Wärmemenge entspricht somit der Enthalpieänderung des Systems, ∆ H = q . Die Temperaturabhängigkeit der Enthalpie bei konstantem Druck ist durch Gl. (2.22b) gegeben, ∆ H = Cp ∆ T . Diese Beziehung stellen wir geeignet um, so dass wir einen Ausdruck für die Temperaturänderung erhalten:
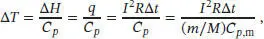
wobei m die Masse, M die Molmasse (von Kupfer) und C p, mdie molare Wärmekapazität bei konstantem Druck ist. Die Endtemperatur des Kupferblocks ist daher
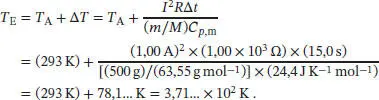
Die Temperaturabhängigkeit der Entropie bei konstantem Volumen ist durch Gl. (3.19) gegeben, S ( T E) = S ( T A) + Cp ln( T E/ T A). Die Entropieänderung des Systems ist daher
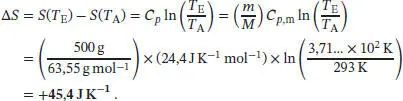
Im zweiten Experiment sind die Anfangs- und Endzustände des Metallblocks identisch, und somit gilt ∆ S = 0. Die gesamte Wärme wird an die Umgebung (d. h. an das Wasserbad) abgegeben, wobei wir davon ausgehen, dass diese hinreichend groß ist, um als unendlich großer Wärmespeicher gelten zu können; die Temperatur des Wasserbads bleibt daher (annähernd) konstant. Für die Entropieänderung erhalten wir
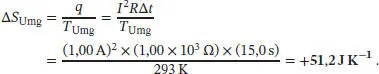
S3.2.9Wie im Hinweis der Aufgabenstellung vorgeschlagen, betrachten wir zunächst die Erwärmung des gefalteten Proteins bei konstantem Druck von der Anfangstemperatur T bis zur Übergangstemperatur T Trans. Die Temperaturabhängigkeit der Entropie bei konstantem Volumen ist durch Gl. (3.19) gegeben, S ( T E) = S ( T A) + Cp ln( T E/ T A). Die Änderung der molaren Entropie, ∆ S m= S m( T E) = S m( T A), bei Schritt 1 ist daher
Читать дальше

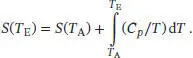
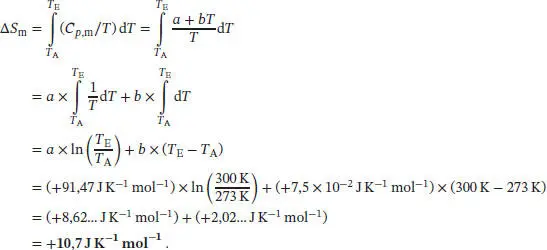
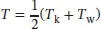
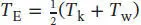 , wie bereits erwähnt.
, wie bereits erwähnt.