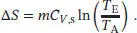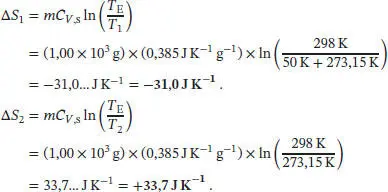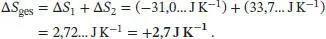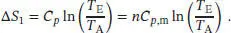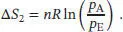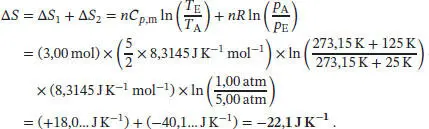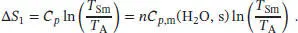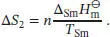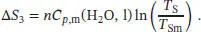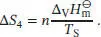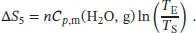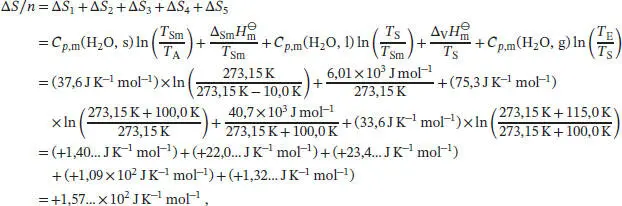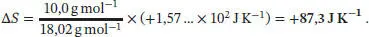James J. Keeler - Arbeitsbuch zu Atkins, de Paula, Keeler Physikalische Chemie

Die Temperaturabhängigkeit der Entropie bei konstantem Volumen ist durch Gl. (3.19) gegeben, ∆ S = CV ln( T E/ T A), wobei hier Cp durch CV ausgetauscht wurde. Unter Einbeziehung der spezifischen Wärme, CV ,S= CV / m , ergibt sich

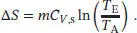
Beachten Sie, dass sich die Innere Energie eines Festkörpers bei Variation des Volumens bzw. des Drucks nicht signifikant verändert, daher können wir CV = Cp = C voraussetzen. Mithilfe dieses Ausdrucks erhalten wir für die Entropieänderungen der beiden Metallblöcke

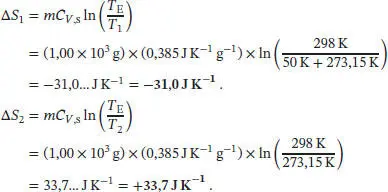
Die Gesamtänderung der Entropie ist

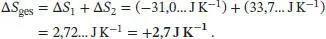
Da ∆ S ges> 0 ist, verläuft dieser Prozess freiwillig, was mit unserer alltäglichen Erfahrung im Einklang steht.

L3.2.6aDa die Entropie eine Zustandsfunktion ist, können wir ∆ S zwischen dem Anfangs- und End-zustand berechnen, indem wir die Zustandsänderung auf einem möglichst bequemen Weg durchführen; in diesem Fall geschieht dies durch Erhitzen bei konstantem Druck mit anschließender Kompression bei konstanter Temperatur. Die Temperaturabhängigkeit der Entropie bei konstantem Volumenist durch Gl. (3.19) gegeben, S ( T E) = S ( T A) + Cp ln( T E/ T A). Die Entropieänderung ∆ S = S ( T E) = S ( T A) beim Erhitzen unter konstantem Druck ist daher

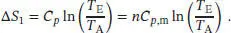
Als Nächstes betrachten wir eine isotherme Änderung des Drucks. Wie in Abschn. 3.1.2a des Lehrbuchs erklärt wird, ist die Entropieänderung bei isothermer Expansion eines idealen Gases durch ∆ S = nR ln( V E/ V A) gegeben. Für eine gleichbleibende Gasmenge bei konstanter Temperatur gilt p ∝ (1/ V ), und somit lautet eine äquivalente Beziehung für diese Entropieänderung

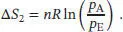
Für die Gesamtänderung der Entropie des Systems erhalten wir daher

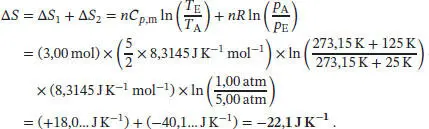
Obwohl ∆ S Sysnegativ ist, kann der Prozess spontan ablaufen, sofern nur ∆ S gespositiv ist.

L3.2.7aDa die Entropie eine Zustandsfunktion ist, können wir ∆ S zwischen dem Anfangs- und Endzustand berechnen, indem wir die Zustandsänderung auf einem möglichst bequemen Weg durchführen. Zunächst betrachten wir die Erwärmung von Eis bei konstantem Druck ausgehend von der Anfangstemperatur T Abis zum Schmelzpunkt T Sm. Die Temperaturabhängigkeit der Entropie bei konstantem Volumen ist durch Gl. (3.19) gegeben, S ( T E) = S ( T A) + Cp ln( T E/ T A). Die Entropieänderung ∆ S = S ( T E) = S ( T A) beim Erhitzen bei konstantem Druck ist daher

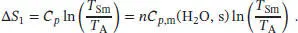
Als Nächstes betrachten wir den Phasenübergang vom Festkörper zur Flüssigkeit bei der Schmelztemperatur T Sm. Die Entropieänderung bei einem Phasenübergang ist durch Gl. (3.16) gegeben, ∆ Trans S = ∆ Trans H / T ' Trans.Damit gilt

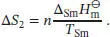
Anschließend wird das flüssige Wasser bis zu seinem Siedepunkt T Serhitzt. Analog zum ersten Schritt schreiben wir

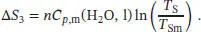
Es folgt der Phasenübergang von der Flüssigkeit zum Gas (in diesem Fall zum Wasserdampf),

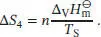
Der entstandene Dampf wird schließlich vom Siedepunt T Sauf die Endtemperatur T Eerhitzt,

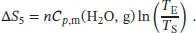
Für die Gesamtänderung der Entropie des Systems (pro Mol H 2O) erhalten wir

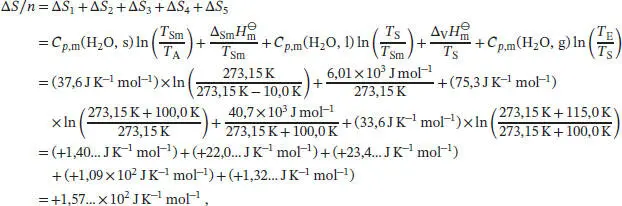
und somit für ursprünglich 10,0 g Eis

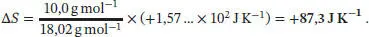
S3.2.1

1 (a) Da die Entropie eine Zustandsfunktion ist, können wir ∆S zwischen dem Anfangs- und Endzustand berechnen, indem wir die Zustandsänderung auf einem möglichst bequemen Weg durchführen.Zunächst betrachten wir die Erwärmung von Wasser bei konstantem Druck ausgehend von der Anfangstemperatur T bis zum Schmelzpunkt TSm. Die Temperaturabhängigkeit der Entropie bei konstantem Volumen ist durch Gl. (3.19) gegeben, S (TE) = S (TA) + Cp ln(TE/TA). Die Entropieänderung bei diesem Schritt ist daherAls Nächstes betrachten wir den Phasenübergang von der Flüssigkeit zum Festkörper bei der Schmelztemperatur TSm. Beachten Sie, dass der Vorgang des Erstarrens bzw. Gefrierens lediglich die Umkehrung eines Schmelzvorgangs ist, daher ist . Die Entropieänderung bei einem Phasenübergang ist durch Gl. (3.16) gegeben, ∆Trans S = ∆Trans H/TTrans. Damit giltAnschließend wird das Eis auf die Endtemperatur T abgekühlt. Analog zum ersten Schritt schreiben wirFür die Gesamtänderung der Entropie des Systems erhalten wirNun betrachten wir die Enthalpieänderung bei diesen drei Schritten. Die Temperaturabhängigkeit der Enthalpie bei konstantem Druck ist durch Gl. (2.22b) gegeben, ∆H = Cp∆T. Für den ersten und den dritten Schritt des zuvor beschriebenen Weges erhalten wirDie Gesamtänderung der Enthalpie des Systems ist daherBei konstantem Druck entspricht die vom System abgegebene Wärme der Enthalpieänderung des Systems, q = ∆H. Wegen qUmg = − q ist die Entropieänderung in der UmgebungDie Gesamtänderung der Entropie ist daherWir sehen, dass dieser Betrag positiv ist (∆Sges > 0), d. h. gemäß dem Zweiten Hauptsatz der Thermodynamik verläuft der Übergang l → s bei −5 °C freiwillig.