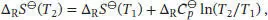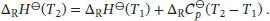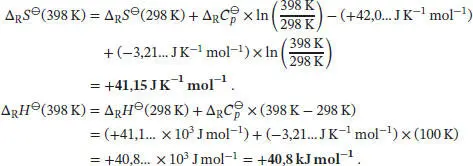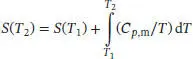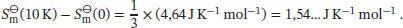
Erhitzen wir die Probe weiter bis zu ihrem Schmelzpunkt, dann beträgt der Anstieg der Entropie
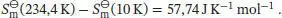
Die Entropieänderung bei einem Phasenübergang ist durch Gl. (3.20b) gegeben, ∆ Trans S ( T Trans) = ∆ Trans H ( T Trans)/ T Trans. Wir erhalten
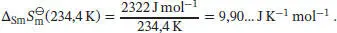
Eine fortgesetzte Erhöhung der Temperatur auf 298,0 K führt zu einem Anstieg der Entropie von
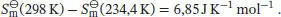
Die molare Entropie nach dem Dritten Hauptsatz bei 298 K ergibt sich aus der Summe der oben genannten Beiträge:
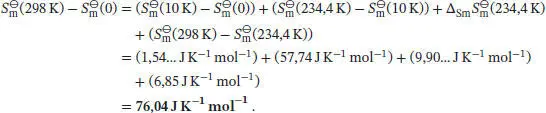
S3.3.3
1 (a) Wenn wir davon ausgehen, dass das Debye’sche T 3-Gesetz angewendet werden kann, dann gilt für die molare Wärmekapazität bei konstantem Druck Cp ,m = aT 3. Die Temperaturabhängigkeit der Entropie ist durch Gl. (3.20a) gegeben,Für eine gegebene Temperatur T ist die Änderung der molaren Entropie, ausgehend vom absoluten Nullpunkt, daherIm vorliegenden Fall erhalten wir für festes Blei bei 10 K
2 (b) Die Entropieänderung wird bestimmt, indem wir die Fläche unter dem Graphen einer Auftragung von (Cp,m/T) gegen T untersuchen, wie sie in Abb. 3.2gezeigt ist.Wir erkennen, dass der Kurvenverlauf einigermaßen ungleichmäßig ist – eine recht gute Anpassung ist jedoch mithilfe von zwei Polynomfunktionen dritten Grades möglich, wobei die erste Funktion den Bereich von 10 K bis 30 K und die zweite den Bereich von 30 K bis 298 K abdeckt. Wenn wir y = (CP,m/T)/(JK−2mol−1) und x = T /K definieren, lässt sich die angepasste Funktion überausdrücken. Die Koeffizienten ci, mit denen die beste Anpassung der Funktion an den Kurvenverlauf in den beiden Temperaturbereichen zustande kommt, sind:Ci10 K bis 30 K30 K bis 298KC3+5,0222 × 10−5−5,2881 × 10−8C2−4,3010 × 10−3+3,5425 × 10−5C1+1,2025 × 10−1−8,1107 × 10−3C0−5,4187 × 10−1+7,5533 × 10−1 Abb. 3.2 T/KCp, m /(JK −1 mol−1)( CP,m/T)/(J K −2 mol−1)102,80,2800157,00,46672010,80,54002514,10,56403016,50,55005021,40,42807023,30,332910024,50,245015025,30,168720025,80,129025026,20,104829826,60,0893Das Integral der angepassten Funktionen im Bereich von xA bis xE lautetDurch Auswahl der jeweils passenden Koeffizienten und Integrationsgrenzen erhalten wir die Lösungen der Integrale für die Entropieänderung in den beiden Bereichen:Die Gesamtänderung der Entropie ergibt sich aus der Summe dieser Werte, somit ist
3 (c) Die Standardentropie von Blei nach dem Dritten Hauptsatz bei 298 K ergibt sich aus der Summe der in Teilaufgabe (b) berechneten Beiträge:Zur Berechnung der Standardentropie von Blei nach dem Dritten Hauptsatz bei 273 K müssen wir den zweiten Teil des Integrals aus Teilaufgabe (b) mit TE = 273 K erneut berechnen:Die übrigen Beiträge bleiben unverändert, und wir erhalten
S3.3.5Die Standardreaktionsentropie ist durch Gl. (3.22b) gegeben, 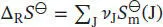 , wobei v Jdie stöchiometrischen Faktoren sind.
, wobei v Jdie stöchiometrischen Faktoren sind.
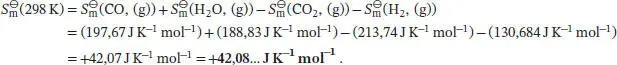
Die Standardreaktionsenthalpie ist durch Gl. (2.30b) gegeben, 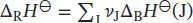 . Unter Beachtung des Vorzeichens von v J(positiv für Produkte, negativ für Reaktanten) schreiben wir
. Unter Beachtung des Vorzeichens von v J(positiv für Produkte, negativ für Reaktanten) schreiben wir
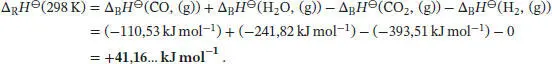
Die Temperaturabhängigkeit der Reaktionsentropie ist durch Gl. (3.24a) gegeben, 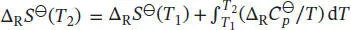 dT, und die Temperaturabhängigkeit der Reaktionsenthalpie ist durch das Kirchhoff’sche Gesetz (Gl. (3.26a)) gegeben,
dT, und die Temperaturabhängigkeit der Reaktionsenthalpie ist durch das Kirchhoff’sche Gesetz (Gl. (3.26a)) gegeben, 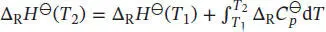 Die Differenz der (molaren) Wärmekapazitäten,
Die Differenz der (molaren) Wärmekapazitäten, 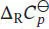 , ist in Gl. (3.24b) definiert als
, ist in Gl. (3.24b) definiert als 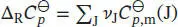
Für die hier betrachtete Reaktion gilt bei 298 K
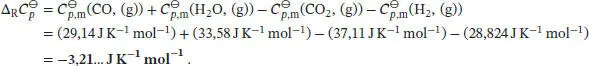
Wenn wir annehmen, dass 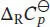 über den gesamten betrachteten Temperaturbereich konstant ist, gilt für die Änderung der Standardreaktionsentropie gemäß Gl. (3.24b)
über den gesamten betrachteten Temperaturbereich konstant ist, gilt für die Änderung der Standardreaktionsentropie gemäß Gl. (3.24b)
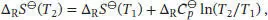
und für die Änderung der Standardreaktionsenthalpie gilt gemäß Gl. (2.32d)
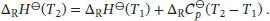
Für die hier betrachtete Reaktion erhalten wir:
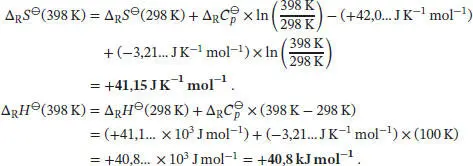
S3.3.7Wenn wir davon ausgehen, dass das Debye’sche T 3-Gesetz angewendet werden kann, dann gilt für die molare Wärmekapazität bei konstantem Druck Cp,m = aT 3. Die Temperaturabhängigkeit der Entropie ist durch Gl. (3.20a) gegeben,
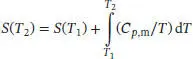
Für eine gegebene Temperatur T ist die Änderung der molaren Entropie, ausgehend vom absoluten Nullpunkt, daher
Читать дальше

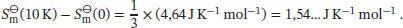
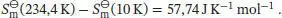
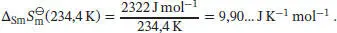
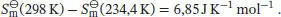
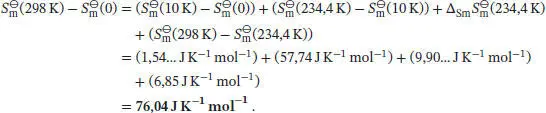
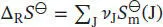 , wobei v Jdie stöchiometrischen Faktoren sind.
, wobei v Jdie stöchiometrischen Faktoren sind.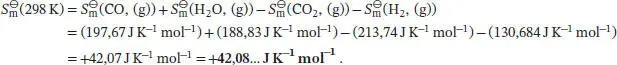
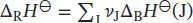 . Unter Beachtung des Vorzeichens von v J(positiv für Produkte, negativ für Reaktanten) schreiben wir
. Unter Beachtung des Vorzeichens von v J(positiv für Produkte, negativ für Reaktanten) schreiben wir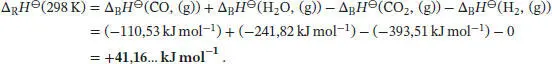
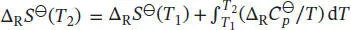 dT, und die Temperaturabhängigkeit der Reaktionsenthalpie ist durch das Kirchhoff’sche Gesetz (Gl. (3.26a)) gegeben,
dT, und die Temperaturabhängigkeit der Reaktionsenthalpie ist durch das Kirchhoff’sche Gesetz (Gl. (3.26a)) gegeben, 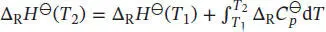 Die Differenz der (molaren) Wärmekapazitäten,
Die Differenz der (molaren) Wärmekapazitäten, 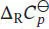 , ist in Gl. (3.24b) definiert als
, ist in Gl. (3.24b) definiert als 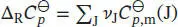
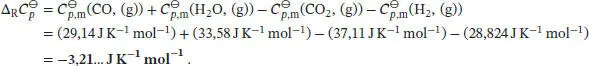
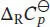 über den gesamten betrachteten Temperaturbereich konstant ist, gilt für die Änderung der Standardreaktionsentropie gemäß Gl. (3.24b)
über den gesamten betrachteten Temperaturbereich konstant ist, gilt für die Änderung der Standardreaktionsentropie gemäß Gl. (3.24b)