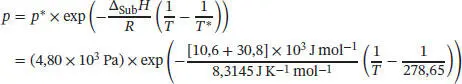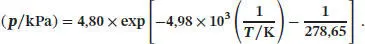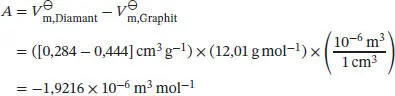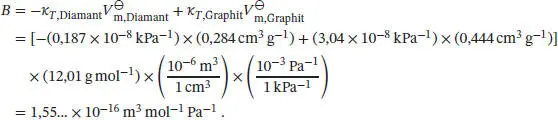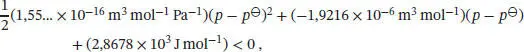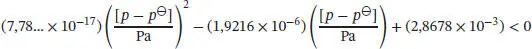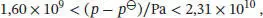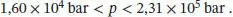James J. Keeler - Arbeitsbuch zu Atkins, de Paula, Keeler Physikalische Chemie

Sublimationsenthalpie ∆ Sub H ersetzt ist. Da ∆ Sub H = ∆ Sm H + ∆ VH gilt, lautet die Beziehung

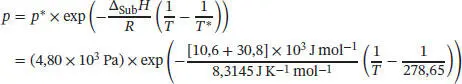
Somit gilt entlang der Fest/Gasförmig-Phasengrenɀe von Benzol der Zusammenhang

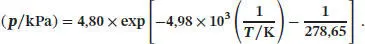
Diese Gleichung beschreibt die Kurve, die in Abb. 4.4für Temperaturen im Bereich unterhalb von T ≤ 278,65 K grafisch aufgetragen ist; die feste Phase und die Gasphase einer Substanz liegen nur bei Temperaturen direkt am und unterhalb des Tripelpunkts im Gleichgewicht vor.

A4.3

1 (a) Wie in der Aufgabenstellung beschrieben, müssen zur Bildung einer α-Helix n − 4 Wasserstoffbrücken entstehen. Wenn jede einzelne dieser Wasserstoffbrückenbindungen eine Bindungsenthalpie von ∆wBHSm beiträgt (d. h., ∆WBHSm ist die Enthalpieänderung, wenn eine dieser Bindungen aufgebrochen wird), dann beträgt die Gesamtänderung der Enthalpie bei der vollständigen Entfaltung einer α-Helix ∆TransH = (n − 4)∆WBHSm.In der Aufgabenstellung wird außerdem erwähnt, dass n − 2 Aminosäuren eine kompakte Helix mit eingeschränkter Beweglichkeit bilden. Wenn sich eine derartige Helix entfaltet, sind diese n − 2 Glieder der Polypeptidkette wieder frei beweglich. Wir wollen die Entropieänderung, die mit dieser „Freisetzung“ jeder einzelnen dieser Aminosäuren verbunden ist, mit ∆WBSSm bezeichnen; die Gesamtänderung der Entropie beträgt dann ∆TransS = (n − 2)∆WBSSm.Die Änderung der Freien Enthalpie bei der Entfaltung der Helix setzt sich aus dem Enthalpieterm und dem Entropieterm zusammen, und wir schreiben

2 (b) Wenn die Schmelztemperatur der Helix erreicht ist, gilt T = TSm und ∆TransG = 0, denn der gefaltete und der entfaltete Zustand liegen im Gleichgewicht vor. Es gilt dannund nach Umstellen ergibt sich

3 (c) In Abb. 4.5ist eine grafische Auftragung von TSm/(∆WBHSm/∆WBSSm) gegen n für 0 ≤ n ≤ 30 gezeigt.Das Verhältnis der unterschiedlichen Werte für TSm, wenn sich die Anzahl der Aminosäuren n um eins erhöht, istDamit dieser Anstieg weniger als 1% beträgt, muss Abb. 4.5 sein, was sich umstellen lässt zuDie möglichen Lösungen für diese quadratische Ungleichung sind n > 16,7 oder n < −11,7. Die Lösung mit dem negativen Vorzeichen können wir verwerfen (denn die Helix kann nicht aus einer negativen Anzahl von Aminosäuren bestehen). Der geringste Wert von n, bei dem sich TSm um weniger als 1% ändert, ist n = 17.

A4.5‡

1 (a) Die Variation der Freien Enthalpie mit dem Druck ist durch Gl. (3.44) gegeben, (∂G/∂p)T = V. Daher muss für die Druckabhängigkeit von ΔRG gelten:

2 (b) Wenn wir die Beziehung aus Teilaufgabe (a) differenzieren und beachten, dass die Definition der isothermen Kompressibilität κT zu (∂V/∂p)T = − κTV umgestellt werden kann, erhalten wir

3 (c) Einsetzen der beiden Beziehungen aus den Teilaufgaben (a) und (b) in die in der Aufgabenstellung gegebene Taylor-Reihe liefertwobei und die molaren Volumina der beiden polymorphen Modifikationen von Kohlenstoff unter Standardbedingungen sind.

4 (d) Die Umwandlung von Graphit in Diamant läuft freiwillig ab, wenn für diesen Prozess ΔRG < 0 gilt. Diese Ungleichung setzen wir, gemeinsam mit den gegebenen Daten, in die Beziehung aus Teilaufgabe (c) ein, wobei wir beachten müssen, dass Vm = VsM gilt (M ist die Molmasse). So erhalten wir

mit

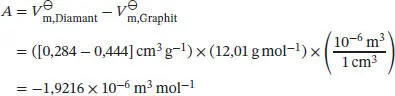
und

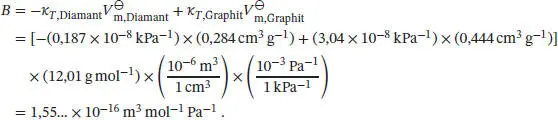
Die resultierende Ungleichung lautet

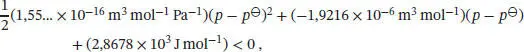
und somit, nach Division durch 1 J mol −1,

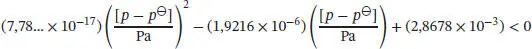
(mit 1 J = 1 Pa m 3). Die Lösung dieser Ungleichung lautet

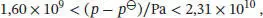
und somit erhalten wir (mit p Ɵ= 1 bar = 10 5Pa)

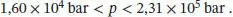
Die Umwandlung von Graphit in Diamant bei 298 K läuft daher bei einem Druck von 1, 60× 104 barfreiwillig ab. Unsere Vorhersage besagt außerdem, dass die Umwandlung bei Drücken oberhalb von 2,31 ×10 5bar nicht mehr freiwillig abläuft. Dies lässt sich dadurch erklären, dass Graphit eine höhere Kompressibilität aufweist als Diamant. Das molare Volumen des Graphits wird daher bei steigendem Druck stärker abnehmen, wodurch Graphit wieder zur thermodynamisch stabileren Phase wird.

Anmerkung: Beachten Sie, dass wir bei dieser Analyse Terme höherer Ordnung in der Taylor-Reihe vernachlässigt haben, die bei sehr hohen Drücken durchaus eine signifikante Rolle spielen können.

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.