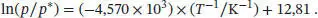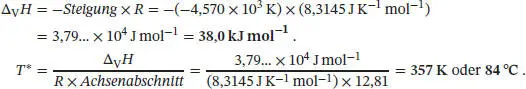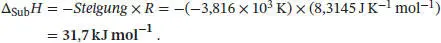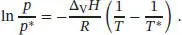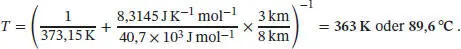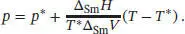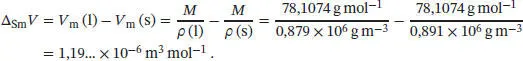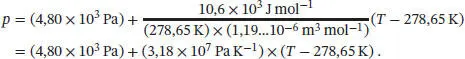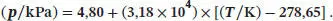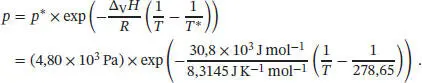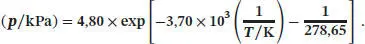Die gegebenen Daten liegen recht präzise entlang einer Geraden; die Gleichung der Ausgleichsgeraden lautet
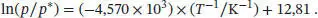
Die Werte von Δ V H und T* lassen sich aus der Steigung bzw. dem Achsenabschnitt bestimmen:
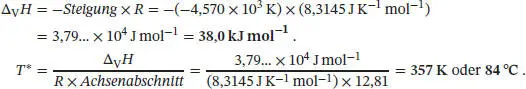
S4.2.11‡
1 (a) Die Clapeyron-Gleichung (Gl. (4.6a)) lautet dp/dT = ∆TransS/∆TransV. Für die Sublimation eines Feststoffs in die Gasphase wird aus dieser Gleichung, mit ∆TransS = ∆TransH/T,Da das molare Volumen eines Gases sehr viel größer ist als das Volumen der gleichen Stoffmenge des entsprechenden Festkörpers, können wir für das Sublimationsvolumen näherungsweise ∆Sub V = Vm (g) − V (s) ≈ Vm (g) schreiben; wenn sich das entstehende Gas ideal verhält, gilt außerdem Vm = RT/p. Einsetzen dieser Beziehung in den obigen Ausdruck liefertMit dx/x = d ln x können wir dafür auch schreiben:
2 (b) Integration der in Teilaufgabe (a) hergeleiteten Gleichung liefert unter der Annahme, dass ∆SubH im betrachteten Bereich temperaturunabhängig ist,Bei einer grafischen Auftragung von ln p gegen 1/T sollte sich eine Gerade mit der Steigung −ΔSubH/R ergeben; eine solche Auftragung ist in Abb. 4.3gezeigt.T/Kp/PaT−1/K-1ln(p/Pa)145,9413,070,006 8522,570147,9618,490,006 7592,917149,9325,990,006 6703,258151,9436,760,006 5823,604153,9750,860,006 4953,929154,9459,560,006 4544,087Die gegebenen Daten liegen recht präzise entlang einer Geraden; die Gleichung der Ausgleichsgeraden lautet
Der Wert für die Sublimationsenthalpie ∆ Sub H lässt sich aus der Steigung −∆ Sub H/R bestimmen:
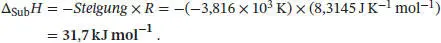
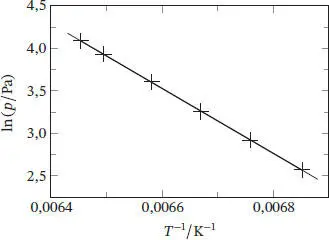
Abb. 4.3
S4.2.13
1 (a) Die Stoffmenge (in mol) des durch die Flüssigkeit perlenden Gases ist nGas = PV/RT, wenn P der Anfangsdruck des Gases und der entweichenden Gasmischung ist. Die Stoffmenge (in mol) des abgeführten Dampfes ist nDampf = m/M. Der Stoffmengenanteil des Dampfes in der Gasmischung ist demzufolge
2 (b) Wenn der Gesamtdruck des Gases P unverändert bleibt, ist der Partialdruck des Dampfes
3 (c) Wenn wir den Zähler und den Nenner des Ausdrucks aus Teilaufgabe (b) durch MPV dividieren, erhalten wir
4 (d) Für Geraniol ist M = 154,2 g mol-1, und mit P = 760 Torr = 1,013 25 x 105 Pa ergibt sichMit den in der Aufgabenstellung gegebenen Daten folgt für den Dampfdruck
S4.2.15Die integrierte Form der Clausius-Clapeyron-Gleichung (Gl. (4.12)) lautet
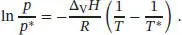
Wir nehmen an, dass sich p* und T* in der Höhe a aus dem Druck p0 bzw. dem Siedepunkt T0 einer Flüssigkeit auf Meereshöhe ergeben. Einsetzen der nach p/p 0= e −a/Humgestellten barometrischen Höhenformel in den obigen Ausdruck ergibt

Für den Siedepunkt von Wasser in einer Höhe von a = 3000 m erhalten wir damit
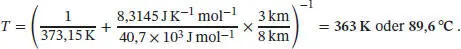
Abschnittsübergreifende Aufgaben
A4.1Die Beziehung zwischen dem Druck p und der Temperatur T entlang einer Fest/Flüssig-Phasengrenze ist durch Gl. (4.9) gegeben,
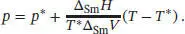
Mit V m =M/ρ erhalten wir für das Schmelzvolumen ∆ Sm V mit den gegebenen Daten
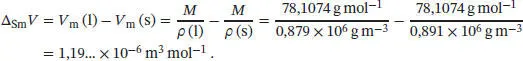
Diesen Wert sowie den gegebenen Wert für ∆ Sm H setzen wir nun in Gl. (4.9) ein. Für den Druck p * und die Temperatur T * setzen wir die gegebenen Werte am Tripelpunkt von Benzol ein, p * = 36 Torr = 4,80 kPa und T * = 5,50 °C = 278,65 K. Wir erhalten
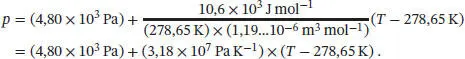
Somit gilt entlang der Fest/Flüssig-Phasengrenze von Benzol der Zusammenhang
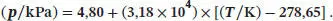
Es ergibt sich eine extrem steil nach rechts ansteigende Linie, die in der Mitte des in Abb. 4.4gezeigten Phasendiagramms vom Tripelpunkt aus nach oben verläuft. Diese Phasengrenzlinie existiert nur für Werte oberhalb von T > T * ( p > p *), da die hier betrachtete Substanz bei Temperaturen unterhalb des Tripelpunkts nicht als Flüssigkeit vorliegen kann. (Hinweis: Dies gilt für die meisten Substanzen - Wasser ist eine wichtige Ausnahme.)
Die Beziehung zwischen dem Druck p und der Temperatur T entlang einer Flüssig/Gasförmig-Phasengrenze ist durch Gl. (4.12) gegeben; für den Druck p* und die Temperatur T * setzen wir erneut die gegebenen Werte am Tripelpunkt von Benzol ein, und wir erhalten
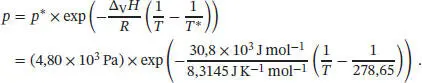
Somit gilt entlang der Flüssig/Gasförmig-Phasengrenze von Benzol der Zusammenhang
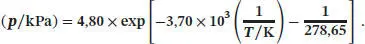
Diese Gleichung beschreibt die Kurve, die in Abb. 4.4in Richtung der rechten oberen Ecke verläuft; diese Phasengrenzlinie ist nur für Werte oberhalb von T ≥ 278,65 K eingetragen, da Benzol bei Temperaturen unterhalb des Tripelpunkts nicht als Flüssigkeit vorliegen kann.
Die Beziehung zwischen dem Druck p und der Temperatur T entlang einer Fest/Gasförmig-Phasengrenɀe ist durch eine Beziehung gegeben, die analog zur Beziehung für die Flüssig/Gasförmig-Phasengrenze aufgebaut ist; der einzige Unterschied ist, dass dort die Verdampfungsenthalpie ∆ V H durch die
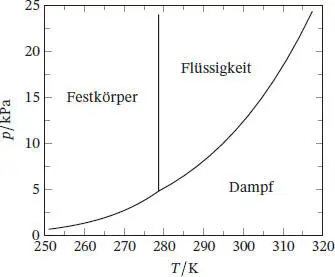
Abb. 4.4
Читать дальше