James J. Keeler - Arbeitsbuch zu Atkins, de Paula, Keeler Physikalische Chemie

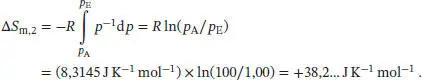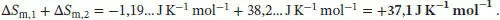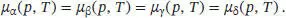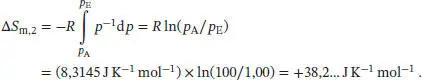
Die Gesamtänderung der Entropie ergibt sich aus der Summe der Entropieänderungen für die beiden Teilschritte,

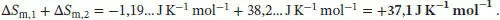
A3.3

1 (a) Die volumenabhängige Variation der Entropie bei konstanter Temperatur ist durch eine der Maxwell-Beziehungen gegeben, die in Tab. 3.5 des Lehrbuchs aufgelistet sind, (∂S/∂V)T = (∂p/∂T)V. Da wir es hier mit molaren Größen zu tun haben, schreiben wir die Van-der-Waals-Zustandsgleichung in der Form damit gilt (∂p/∂T)V = R/(Vm − b). Durch Integration erhalten wirwobei wir den Wert für b dem Anhang des Lehrbuchs entnommen haben. Beachten Sie die Einheiten der molaren Volumina, die hier in dm3 mol − 1 angegeben sind, d. h. in den gleichen Einheiten wie der Van-der-Waals-Koeffizient b.

2 (b) Die temperaturabhängige Variation der Entropie bei konstantem Volumen bzw. konstantem Druck ist durch die Beziehungengegeben. Bei beiden Beziehungen wird vorausgesetzt, dass sich die Wärmekapazitäten im betrachteten Temperaturbereich nicht ändern.Der Gleichverteilungssatz (siehe „Toolkit 7: Der Gleichverteilungssatz“ in Abschn. 2.1des Lehrbuchs) kann verwendet werden, um den Wert von CV ,m abzuschätzen; für ein ideales Gas gilt Cp,m = CV,m + R. Atome besitzen lediglich drei Freiheitsgrade der Translation, und es gilt sowie Lineare Kreisel besitzen zwei zusätzliche Freiheitsgrade der Rotation, und somit gilt sowie . Nichtlineare Kreisel besitzen sogar drei Freiheitsgrade der Rotation, und es gilt CV ,m = 3 R sowie Cp,m = 4 R.In Abb. 3.8und 3.9sind Auftragungen von ∆Sm/R gegen ln(T2/T1) bei konstantem Volumen bzw. konstantem Druck gezeigt.

3 (c) Die temperaturabhängige Änderung der Entropie ist in Gl. (3.18) gegeben; durch Integration erhalten wir eine geeignete Form dieser Beziehung, um die in der Aufgabenstellung erwähnte Form der Wärmekapazität nutzen zu können: Abb. 3.8 Abb. 3.9 Um dieses Ergebnis auf bequeme Weise zu analysieren, betrachten wir einen definierten Temperaturbereich, z. B. von 273 K bis 473 K, und erstellen eine Auftragung der Beiträge der drei Terme als Funktion der jeweils relevanten Parameter a, b und c. Dem Anhang des Lehrbuchs entnehmen wir folgende (physikalisch sinnvolle) Bereiche für diese drei Parameter: für a wählen wir den Bereich von 15 J K−1 mol−1 bis 80 J K−1 mol−1; für b wählen wir den Bereich von 0 bis 50 × 10−3 J K−2 mol−1; für c wählen wir den Bereich von –10 × 105 J K−1 mol−1 und +2,0 × 105JK−1 mol−1.In Abb. 3.10sind die Beiträge der drei Terme über den hier gewählten Temperaturbereich gezeigt; wir erkennen, dass Term 1 den mit Abstand größten Beitrag zur Entropieänderung liefert. Außerdem erkennen wir, dass die Beiträge der Terme 1 und 2 in einem Anstieg der Entropie mit der Temperatur resultieren. Term 3 führt hingegen zu einem negativen Beitrag zur Entropieänderung – zumindest dann, wenn c < 0 ist, was typischerweise der Fall ist.

4 (d) Die Temperaturabhängigkeit der Freien Enthalpie bei konstanter Temperatur ist durch Gl. (3.44b) gegeben, (∂ G /∂ p)T = V. Die physikalische Bedeutung dieses partiellen Differenzials ist – wie wir Abb. 3.10 Abb. 3.11 unmittelbar sehen – dass diese Größe dem Volumen des Systems entspricht. Für ein ideales Gas gilt V = nRT/p; nach Integration erhalten wir daher einfach ∆G = nRT ln(pE/pA), was Gl. (3.50) entspricht. In Abb. 3.11ist eine Auftragung von ∆G/nRT gegen pE /pA gezeigt. Wir erkennen, dass die Freie Enthalpie bei konstant gehaltener Temperatur mit dem Druck ansteigt.

5 (e) Die Abhängigkeit des Fugazitätskoeffizienten vom Kompressionsfaktor Z ist durch die folgende Beziehung gegeben:Nun drücken wir die Größen Druck, Volumen und Temperatur über die reduzierten Variablen pr , Vr und Tr aus; wir schreibenwobei die kritischen Werte von p, V und T gegeben sind durchFür den Kompressionsfaktor Z können wir daher schreiben:Unser Ziel ist, Z ausschließlich in Abhängigkeit von Vr und Tr auszudrücken; daher ersetzen wir pr durchund schreiben damitDie zu integrierende Variable ist der Druck p, laut Aufgabenstellung soll allerdings Vr näher untersucht werden; wir benötigen daher die folgende Ableitung:Als untere Integrationsgrenze wählen wir p = 0, was Vr = ∞ entspricht. Das zu untersuchende Integral lautet somitDieses komplexe Integral lässt sich am einfachsten mithilfe mathematischer Software lösen. In Abb. 3.12sind einige repräsentative Ergebnisse für den Fugazitätskoeffizienten ɸ als Funktion von Vr für unterschiedliche Werte von Tr gezeigt. Abb. 3.12

Behandeln Sie alle Gase als ideal, sofern nicht ausdrücklich etwas anderes verlangt ist. Thermochemische Daten sind für 298,15 K angegeben, sofern nicht ausdrücklich etwas anderes erwähnt ist.

Die mit dem Symbol ‡ gekennzeichneten Aufgaben wurden von Charles Trapp und Carmen Giunta beigesteuert.

D4.1.1Das chemische Potenzialist die zentrale Funktion, die die Stabilität von Phasen bestimmt. Die Phase, deren chemisches Potenzial unter den gegebenen Bedingungen am geringsten ist, ist am stabilsten. Wenn zwei oder mehr Phasen bei bestimmten Bedingungen dieselben chemischen Potenziale besitzen, dann liegen sie unter diesen Bedingungen im Gleichgewicht vor. Wenn man weiß, wie die chemischen Potenziale von den Bedingungen (Temperatur, Druck, in späteren Kapiteln auch Zusammensetzung) abhängen, kann man die chemischen Potenziale für verschiedene Phasen berechnen und Bedingungen für ihre Stabilität sowie für Gleichgewichte zwischen ihnen angeben.

D4.1.3Damit zwei Phasen im Gleichgewicht vorliegen können, müssen die chemischen Potenziale aller Komponenten, aus denen diese beiden Phasen bestehen, identisch sein. In einem Einkomponentensystemmuss das chemische Potenzial dieser einzigen Komponente in allen Phasen, die miteinander im Gleichgewicht stehen, identisch sein. Das chemische Potenzial ist eine Funktion von zwei Variablen, p und T (und nicht der Zusammensetzung). Daher gilt: Wenn vier Phasen α, ß, γ und δ miteinander im Gleichgewicht stehen, müssen deren chemischen Potenziale folgende Bedingungen erfüllen:

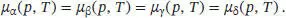
Dies ist ein Satz aus unabhängigen Gleichungen, die nur zwei Variablen aufweisen (p und T), und die nicht miteinander kompatibel sind.

L4.1.1aJede einzelne Fläche in einem Phasendiagramm repräsentiert eine einzelne Phase, während Linien die Phasengrenzen anzeigen, entlang derer zwei Phasen im Gleichgewicht koexistieren. Punkt a liegt in einer Fläche, also existiert hier nur eine Phase. Die Punkte b und d l iegen auf Linien, also liegen hier zwei Phasenvor. An Punkt c stehen drei Phasenmiteinander im Gleichgewicht.

L4.1.2aWenn eine infinitesimal kleine Menge dn einer Substanz von einem Bereich in einen anderen gebracht wird, ist die Änderung der Freien Enthalpie (siehe Abschn. 4.1.1c des Lehrbuchs)