James J. Keeler - Arbeitsbuch zu Atkins, de Paula, Keeler Physikalische Chemie

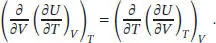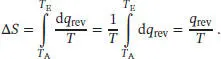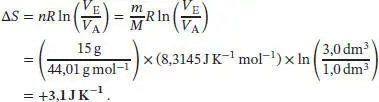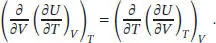
In Abschn. 2.4.2 des Lehrbuchs wird erklärt, dass für ein ideales Gas (∂ U/ ∂ V ) T= 0 gilt. Mit dem obigen Ausdruck folgt somit unmittelbar, dass (∂ CV/ ∂ V ) T= 0gelten muss.

A2.7

1 (a) Die bei einer isothermen reversiblen Expansion verrichtete Arbeit ist gemäß Gl. (2.8b) durch das Integral p dV gegeben, wobei p der Druck des Gases ist. Die Zustandsgleichung für ein Van-der-Waals-Gas (Gl. 1.27a) lautet p = nRT/(V − nb) − an2/V2. Die Aufgabe besteht darin, mithilfe dieser Beziehung für den Druck das Integral zwischen den Integrationsgrenzen VA und VE zu lösenMithilfe der in der Aufgabenstellung gegebenen Daten sowie den Van-der-Waals-Konstanten für CO2 aus dem Anhang des Lehrbuchs erhalten wir für die bei der Expansion verrichtete ArbeitDiese Arbeit lässt sich in der gewohnten Einheit Joule (J) ausdrücken, indem wir den Druck und das Volumen in SI-Einheiten angeben:Dabei haben wir 1 Pa m3 = 1N m−2 m3 = 1N m = 1 J verwendet. Wenn wir davon ausgehen, dass sich das Gas ideal verhält, erhalten wir für die verrichtete Arbeit nRT1n VE/VA= −2,7kJ. Die Nichtidealität des Gases sorgt also für eine signifikante Änderung der verrichteten Arbeit (auch wenn sie in diesem Fall nicht besonders drastisch ausfällt).

2 (b) In einem reversiblen adiabatischen Prozess hängen Anfangs- und Enddruck gemäß Gl. (2.50) zusammen, , wobei γ das Verhältnis der Wärmekapazitäten ist, γ = Cp,m/CV,m. Für eineinatomiges Gas ist , und für ein mehratomiges Gas, bei dem ausschließlich die Translationsund die Rotationsfreiheitsgrade zur Wärmekapazität beitragen, ist .Zur allgemeinen Untersuchung der Abhängigkeit des Drucks vom Volumen reicht es aus, pA = 1 und VA = 1 zu setzen (in beliebigen Einheiten) und für beide genannten Fälle eine Auftragung von pE/(1) = (1/VE)γ zu erstellen; eine solche Auftragung ist in Abb. 2.4gezeigt. Abb. 2.4 Wie erwartet schneiden sich die beiden Adiabaten bei VE/VA = 1. Die Volumenabhängigkeit des Drucks lässt sich aus der Steigung der Adiabate ablesen; in der Abbildung erkennen wir, dass diese Abhängigkeit bei einer Vergrößerung des Volumens immer schwächer ausgeprägt ist. Für typische Werte von γ ist der Einfluss auf den Verlauf der Adiabate eher gering. Beachten Sie, welche der beiden in Abb. 2.4gezeigten Adiabaten bei VE/VA = 1 die größere Steigung besitzt.

Behandeln Sie alle Gase als ideal, sofern nicht ausdrücklich etwas anderes verlangt ist. Thermochemische Daten sind für 298,15 K angegeben, sofern nicht ausdrücklich etwas anderes erwähnt ist.

Die mit dem Symbol ‡ gekennzeichneten Aufgaben wurden von Charles Trapp und Carmen Giunta beigesteuert.

D3.1.1Der Zweite Hauptsatz besagt nur, dass die Gesamtentropie von System (d. h. der Moleküle in den Zellen) und Umgebung (also dem Medium um das System herum) in einem freiwillig ablaufenden Prozess zunehmen muss. Er sagt nicht, dass die Entropie in einem Teil des Universums zunehmen muss, der mit seiner Umgebung in Wechselwirkung steht. Im vorliegenden Fall wachsen die Zellen, indem sie ihrer Umgebung (dem Medium) chemische Energie entnehmen; bei diesem Prozess überwiegt die Zunahme der Entropie im Medium die Abnahme der Entropie im System. Damit ist der Zweite Hauptsatz nicht verletzt.

D3.1.3In Abschn. 3.1.1 des Lehrbuchs finden Sie eine ausführliche Diskussion der Beziehungen zwischen den unterschiedlichen Formulierungen des Zweiten Hauptsatzes der Thermodynamik. Wir wollen hier eine kurze Zusammenfassung geben. Die beiden wichtigsten Formulierungen des Zweiten Hauptsatz treffen äquivalente Aussagen, die auf direkten Beobachtungen beruhen:

1 (a) Formulierung von Kelvin: Ein Prozess, bei dem lediglich Wärme aus einem Reservoir entnommen und vollständig in Arbeit umgewandelt wird, ist unmöglich.

2 (b) Formulierung von Clausius: Wärme fließt niemals von einem kälteren zu einem wärmeren Objekt, die miteinander in Kontakt stehen.

Man kann zeigen, dass diese Formulierungen äquivalent sind, und dass beide zu der Schlussfolgerung führen, dass eine Zustandsfunktion des Systems existieren muss, die man die Entropie S nennt. Die Entropie ist durch die Beziehung d S = d q rev /T definiert. Man kann zeigen, dass d S ein totales Differenzial ist, d.h. ʃ d S = 0. Die Entropie S ist daher eine Zustandsgröße, die jedes System aufweisen muss.

Die soeben formulierte Definition führt uns zur Clausius’schen Ungleichung, d S ≥ d q/T (Gl. (3.11)), wobei d q die Wärmemenge repräsentiert, die bei einem realen – notwendigerweise irreversiblen - Prozess übertragen wird. In einem abgeschlossenen System (d. h. einem System, dass von seiner Umgebung vollständig isoliert ist) gilt d q = 0, und nach der Clausius’schen Ungleichung ist dann d S ≥ 0 (Gl. (3.12)). Daraus folgt, dass die Entropie in einem abgeschlossenen (isolierten) System bei einem freiwillig ablaufenden Prozess niemals abnehmen kann. Da wir das Universum in seiner Gesamtheit als isoliertes System auffassen können, würde dies bedeuten, dass ∆ S ges= ∆ S Sys+ ∆ S Umg≥ 0 ist – diese Ungleichung ist eine alternative Schreibweise für den Zweiten Hauptsatz der Thermodynamik.

L3.1.1aDamit der beschriebene Prozess freiwillig ablaufen kann, muss er irreversibel sein und der Clausius’schen Ungleichung gehorchen, d. h. es muss ∆ S ges= ∆ S Sys+ ∆ S Umg≥ 0 gelten (anstelle von AS Sysschreiben wir in aller Regel kurz AS). Im hier beschriebenen Fall ist ∆ S ges= 125 J K −1+ (−125 J K −1) = 0. Daraus folgt, dass der Prozess nicht freiwilligablaufen kann, und zwar in keiner der möglichen Richtungen; das System befindet sich im Gleichgewicht.

L3.1.2aDie thermodynamische Definition der Entropie ist durch Gl. (3.1a) gegeben, d S = d q rev/ T , und für eine endliche, messbare Änderung (bei konstanter Temperatur) gilt

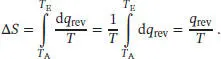
Wir nehmen an, dass der Metallblock so groß ist, dass sich seine Temperatur durch die Wärmezufuhr nicht wesentlich ändert, daher ist q rev= 100 kJ.

1 (i) Bei 0 °C ist die Änderung der Entropie

2 (ii) Bei 50 °C ist die Änderung der Entropie

L3.1.3aWie in Abschn. 3.1.2a des Lehrbuchs erklärt wird, berechnet man die Entropieänderung für die isotherme Expansion eines Gases gemäß ∆ S = nR ln( V E/ V A). Damit erhalten wir

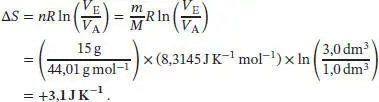
L3.1.4aWie in Abschn. 3.1.2a des Lehrbuchs erklärt wird, berechnet man die Entropieänderung für die isotherme Expansion eines Gases gemäß ∆ S = nR ln( V E/ V A). Bei einer Verdopplung des Volumens ist V E/ V A= 2.

1 (i) Isotherme reversible Expansion:Da es sich um einen reversiblen Prozess handelt, ist ∆Sges = 0. Wegen ∆Sges = ∆S + ∆SUmg ist in diesem Fall