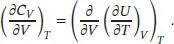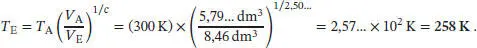
Die bei adiabatischer Expansion eines idealen Gases verrichtete Arbeit ist nach Gl. (2.48):
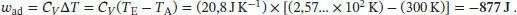
L2.5.4aBei einer reversiblen adiabatischen Zustandsänderung wird nach Gl. (2.48) die Arbeit w ad= CV ΔT geleistet. Die Aufgabe besteht zunächst darin, Δ T zu finden. In einem reversiblen adiabatischen Prozess hängen die Anfangs- und Endzustände gemäß Gl. (2.49b) zusammen, 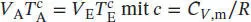 . Für ein ideales Gas gilt gemäß Gl. (2.25) Cp ,m− CV ,m= R , und somit
. Für ein ideales Gas gilt gemäß Gl. (2.25) Cp ,m− CV ,m= R , und somit
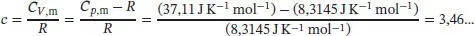
Für die Temperaturänderung Δ T gilt
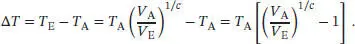
Die verrichtete Arbeit ist daher
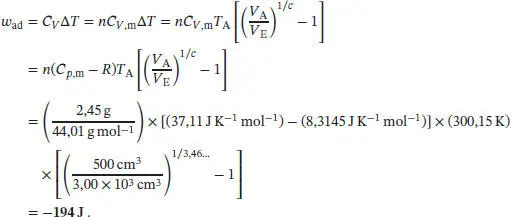
L2.5.5aFür eine reversible adiabatische Expansion gilt nach Gl. (2.50) 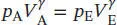 Damit ist der gesuchte Enddruck
Damit ist der gesuchte Enddruck
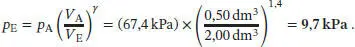
S2.5.1Bei einer reversiblen adiabatischen Zustandsänderung wird nach Gl. (2.48) die Arbeit w ad= C VΔ T geleistet. Die Anfangs- und Endzustände hängen gemäß Gl. (2.49b) zusammen, 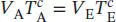 mit c = CV , m/ R . Für ein ideales Gas gilt gemäß Gl. (2.25) Cp , m– CV , m= R , und somit
mit c = CV , m/ R . Für ein ideales Gas gilt gemäß Gl. (2.25) Cp , m– CV , m= R , und somit
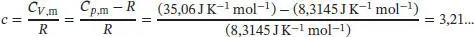
Die Endtemperatur ist
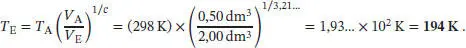
Die verrichtete Arbeit ist
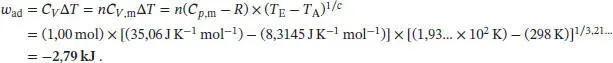
Die Arbeit ist in diesem Fall identisch mit der Änderung der Inneren Energie,
Abschnittsübergreifende Aufgaben
A2.1Eine Zustandsfunktion beschreibt eine thermodynamische Größe, deren Wert unabhängig ist von dem Weg, den das System beschritten hat, um diesen Zustand zu erreichen. Beispiele für Zustandsfunktionen sind der Druck, die Temperatur, die Innere Energie und die Enthalpie, außerdem die thermodynamischen Eigenschaften, die in Fokus 3 des Lehrbuchs beschrieben sind: die Entropie, die Freie Enthalpie (auch Gibbs-Energie) und die Freie Energie (auch Helmholtz-Energie). Die Differenziale von Zustandsfunktionen sind exakt; daher können wir die mathematischen Eigenschaften von totalen Differenzialen nutzen, um weitreichende Schlussfolgerungen über die Beziehungen zwischen physikalischen Größen zu ziehen. Hierbei ergeben sich mitunter Zusammenhänge, die zunächst unerwartet erscheinen mögen, jedoch von weitreichender Bedeutung sind.
Von besonderer Bedeutung für praktische Anwendungen ist die Erkenntnis, dass der Wert einer uns interessierenden physikalischen Größe durch direkte Kombination von Messergebnissen anderer Größen direkt bestimmt werden kann. Dadurch ist es unerheblich, ob für die Bestimmung der eigentlich gesuchten Größe überhaupt eine experimentelle Methode existiert; in anderen Fällen kann eine solche Methode zwar durchaus verfügbar, aber technisch höchst schwierig umzusetzen oder mit großen Ungenauigkeiten behaftet sein. Durch den beschriebenen „Umweg“, stattdessen andere Größen zu messen und die Ergebnisse mathematisch zu kombinieren, können derartige Probleme umgangen werden.
A2.3Die Änderung der (Standard-)Reaktionsenthalpie in Abhängigkeit von der Temperatur wird durch das Kirchhoff’sche Gesetz, Gl. (2.32a), beschrieben. Wenn wir davon ausgehen, dass die Wärmekapazitäten im betrachteten Temperaturbereich konstant sind, können wir die integrierte Form des Kirchhoff’schen Gesetzes, Gl. (2.32d), verwenden:
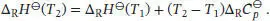
Wir erkennen, dass das Vorzeichen der Enthalpieänderung davon abhängt, welches Vorzeichen die Differenz der molaren Wärmekapazitäten der Produkte und der Reaktanten bei konstantem Druck, 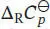 , aufweist: ein negativer Wert von
, aufweist: ein negativer Wert von 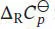 zeigt eine Abnahme, ein positiver Wert eine Zunahme der Standardreaktionsenthalpien an, wenn die Temperatur sich erhöht.
zeigt eine Abnahme, ein positiver Wert eine Zunahme der Standardreaktionsenthalpien an, wenn die Temperatur sich erhöht.
1 (a) Wenn wir für die Reaktiongemäß den Informationen aus der Aufgabenstellung davon ausgehen, dass wir näherungsweise für die molaren Wärmekapazitäten bei konstantem Druck von 4R für Wasserdampf und von für Wasserstoff- und Sauerstoffgas annehmen können, dann erhalten wir, mit Gl. (2.32b),Die Differenz ist negativ, , d.h. wir können davon ausgehen, dass die Standardreaktionsenthalpie mit der Temperatur abnimmt.
2 (b) Für die Reaktionerhalten wir in analoger Weise zu Teilaufgabe (a)Die Differenz ist positiv, , d. h. wir können davon ausgehen, dass die Standardreaktionsenthalpie mit der Temperatur zunimmt.
3 (c) Für die Reaktionerhalten wir in analoger Weise zu den Teilaufgaben (a) und (b)Die Differenz ist negativ, −6R < 0, d. h. wir können davon ausgehen, dass die Standardreaktionsenthalpie mit der Temperatur abnimmt.
A2.5Die Wärmekapazität bei konstantem Volumen ist in Gl. (2.14) definiert als CV = (∂ U / ∂ T ) V. Daraus folgt
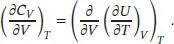
Durch Anwendung der in der Aufgabenstellung genannten Regel für partielle Ableitungen ergibt sich daraus
Читать дальше

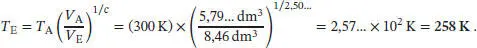
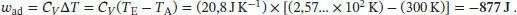
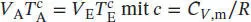 . Für ein ideales Gas gilt gemäß Gl. (2.25) Cp ,m− CV ,m= R , und somit
. Für ein ideales Gas gilt gemäß Gl. (2.25) Cp ,m− CV ,m= R , und somit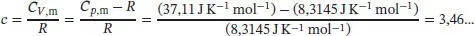
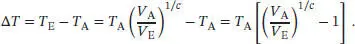
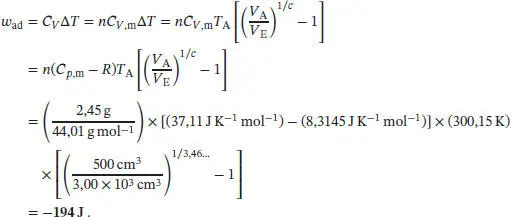
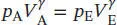 Damit ist der gesuchte Enddruck
Damit ist der gesuchte Enddruck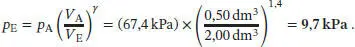
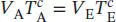 mit c = CV , m/ R . Für ein ideales Gas gilt gemäß Gl. (2.25) Cp , m– CV , m= R , und somit
mit c = CV , m/ R . Für ein ideales Gas gilt gemäß Gl. (2.25) Cp , m– CV , m= R , und somit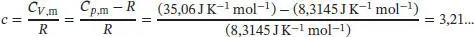
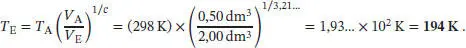
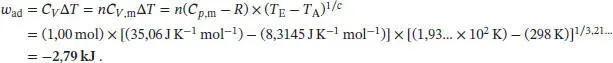
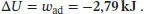
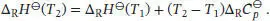
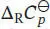 , aufweist: ein negativer Wert von
, aufweist: ein negativer Wert von 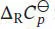 zeigt eine Abnahme, ein positiver Wert eine Zunahme der Standardreaktionsenthalpien an, wenn die Temperatur sich erhöht.
zeigt eine Abnahme, ein positiver Wert eine Zunahme der Standardreaktionsenthalpien an, wenn die Temperatur sich erhöht.