James J. Keeler - Arbeitsbuch zu Atkins, de Paula, Keeler Physikalische Chemie

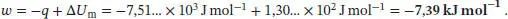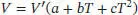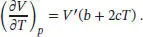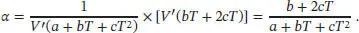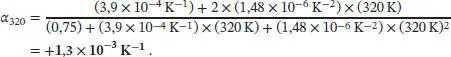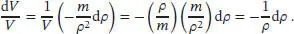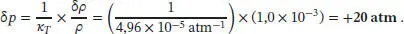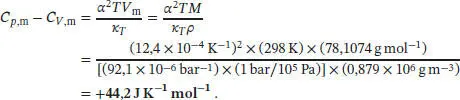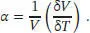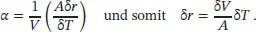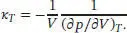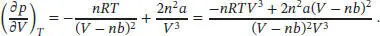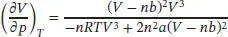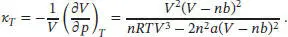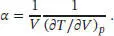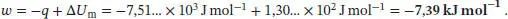
L2.4.3aDas Volumen einer Flüssigkeit kann durch die Beziehung

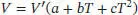
beschrieben werden, wobei im vorliegenden Fall a = 0,75, b = 3,9 × 10 −4K −1und c = 1,48 X10 −6K −2ist. Der Koeffizient der thermischen Ausdehnung α ist in Gl. (2.40) definiert als α. = (1/ V ) (∂ V / ∂ T ) p. Die Ableitung nach T lautet dann

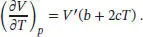
Damit folgt

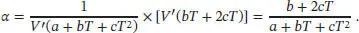
Die Lösung dieses Ausdrucks für T = 320 K ist

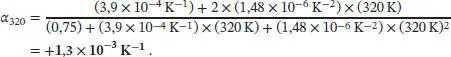
L2.4.4aDie isotherme Kompressibilität ist in Gl. (2.41) definiert, κ T= −(1/ V )( ∂ V / ∂ p ) T. Bei konstanter Temperatur gilt d V / V = −κ Td p . In dieser Aufgabe wird nach der Änderung der Dichte gefragt, daher müssen wir zunächst das Volumen V über die Dichte ρ (rho) ausdrücken. Es gilt V = m/ρ, wobei m die Masse ist, und somit gilt dV = (− m /ρ 2)d ρ . Wir schreiben

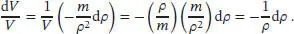
Daraus folgt

Diese Beziehung gibt den Zusammenhang zwischen einer Änderung des Drucks und der Änderung der Dichte an. Für kleine Änderungen ist es zulässig, die Differenziale d ρ und d ρ näherungsweise durch die Differenzen δ ρ und δ p zu ersetzen. Der gesuchte Druck ist demnach

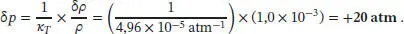
L2.4.5aDie Differenz zwischen den molaren Wärmekapazitäten ist durch Gl. (2.45) gegeben, C p, m− C v , m= α 2 TV m/κ T. Das molare Volumen V mlässt sich über die Dichte ρ (rho) und die molare Masse M ausdrücken, V m= M/ ρ . Die Werte für α, κ und ρ von Benzol finden Sie im Anhang des Lehrbuchs, und wir erhalten

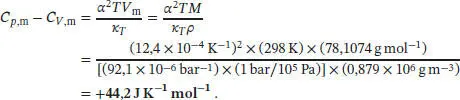
Die Einheiten sind K −1Pam 3mol −1= K −1(Nm −2)m 3mol −1= K −1N m mol −1= JK −1mol −1.

S2.4.1‡Der Koeffizient der thermischen Ausdehnung ist in Gl. (2.40) definiert als α = (1/V)( ∂ V /∂ T ) p. Für hinreichend kleine Änderungen des Volumens und der Temperatur können wir die beiden partiellen Differenziale näherungsweise durch die Differenzen δV und δT ersetzen,

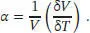
Mit der Näherung δV≈ Aδr aus dem Hinweis in der Aufgabenstellung ergibt sich

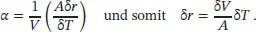
Aus Tab. 2.8 in Abschn. 2.4des Lehrbuchs entnehmen wir für Wasser den Wert α = 2,1 × 10 −4K −1. Für eine Temperaturerhöhung von 1,0 °C erhalten wir

Da Δr α Δ T ist, ergibt sich für eine Temperaturerhöhung um 2,0 °C ein Anstieg des Meeresspiegels um Δr = 1, 6 m, und für eine Temperaturerhöhung um 3,5 °C erhalten wir Δ r = 2, 8 m.

Beachten Sie, dass wir bei dieser Berechnung angenommen haben, dass die Gesamtfläche der Weltmeere bei einem Anstieg des Meeresspiegels konstant bleibt, und dass die Ozeane aus reinem Wasser bestehen, d. h. α(H 2O) = α(Ozean).

S2.4.3

1 (a) Wenn V = V(p, T) ist, giltWenn p = p(V, T) ist, gilt

2 (b) Wenn wir den Ausdruck für dV aus Teilaufgabe (a) durch V dividieren, erhalten wirDie isotherme Kompressibilität ist in Gl. (2.41) definiert, κT = −(1/V)( ∂V/∂p)T. Der Koeffizient der thermischen Ausdehnung ist in Gl. (2.40) definiert als α = (1/V)(∂V/∂T)p. Mit diesen beiden Beziehungen ergibt sich, wenn wir außerdem (1 /V) dV in d ln V umformulieren,Wenn wir den Ausdruck für dp aus Teilaufgabe (a) durch p dividieren, erhalten wirSomit giltHinweis: Um von Zeile 1 nach Zeile 2 zu gelangen, wurden die Identität (1/x) dx = d ln x sowie die Euler’sche Kettenregel verwendet. Um von Zeile 3 nach Zeile 4 zu gelangen, wurden Kehrwerte gebildet. Um von Zeile 4 nach Zeile 5 zu gelangen, wurde die Definition von κT verwendet. Um von Zeile 5 nach Zeile 6 zu gelangen, wurde die Definition von α verwendet.

S2.4.5Die isotherme Kompressibilität ist in Gl. (2.41) definiert, κ T= −(1 /V )(∂ V/ ∂ p ) T. Unter Verwendung der Kehrwert-Identität können wir auch schreiben:

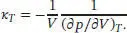
Für den Druck eines Van-der-Waals-Gases gilt p = nRT/ ( V − nb ) − n2a/V2, und somit ist

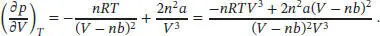
Es folgt

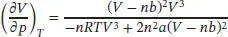
und somit

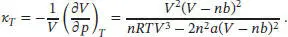
Der thermische Expansionskoeffizient ist in Gl. (2.40) definiert, α T= (1 /V )(∂ V/ ∂ T ) p. Unter Verwendung der Kehrwert-Identität können wir auch schreiben:

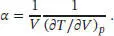
Durch Umstellen der Van-der-Waals-Gleichung (Gl. 1.27a) ergibt sich