James J. Keeler - Arbeitsbuch zu Atkins, de Paula, Keeler Physikalische Chemie

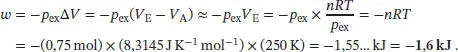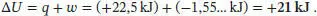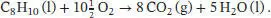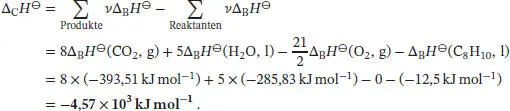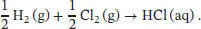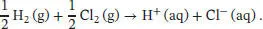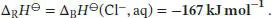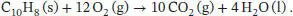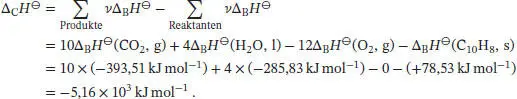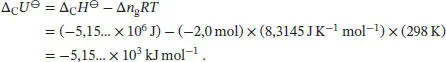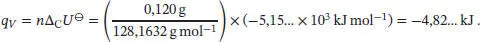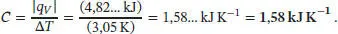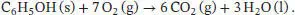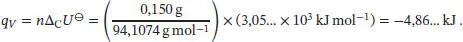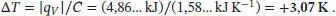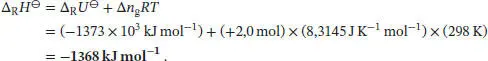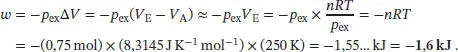
Mithilfe des Ersten Hauptsatzes der Thermodynamik (Gl. (2.2)) erhalten wir

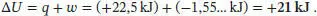
L2.3.2aDie Reaktionsgleichung für die Bildung von Ethylbenzol lautet

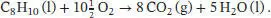
Zur Berechnung der Standardverbrennungsenthalpie dieser Verbindung setzen wir die angegebene Standardbildungsenthalpie Δ B H ⊖sowie weitere Werte aus Tab. 2.11 aus dem Anhang des Lehrbuchs in Gl. (2.30a) ein. Für die Standardverbrennungsenthalpie erhalten wir

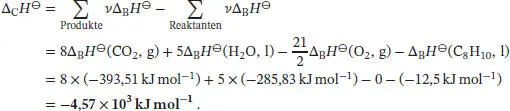
L2.3.3aDie Standardbildungsenthalpie Δ B H ⊖von HCl (aq) entspricht der Standardreaktionsenthalpie Δ R H ⊖der Reaktion

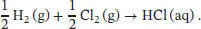
Da es sich bei HCl um eine starke Säure handelt, lautet die effektive Reaktion

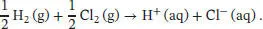
Per Definition ist Δ B H ⊖(H +, aq) = 0, daher entspricht Δ R H ⊖dieser Reaktion der Standardbildungsenthalpie der Chloridionen, Δ B H ⊖(Cl −, aq):

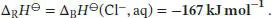
L2.3.4aDie Reaktionsgleichung für die Verbrennung von Naphthalin lautet

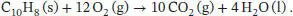
Die Standardverbrennungsenthalpie Δ CH ⊖berechnen wir mithilfe von Gl. (2.30a) unter Verwendung der thermochemischen Daten, die in Tab. 2.10 und 2.11 im Anhang des Lehrbuchs angegeben sind:

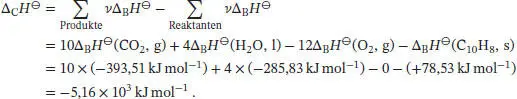
In einem Bombenkalorimeter findet die Wärmeübertragung bei konstantem Volumen statt; die Wärmemenge ist daher durch q V= n Δ C U ⊖gegeben. Δ C U ⊖und Δ C H ⊖hängen über die in Gl. (2.20) angegebene Beziehung zusammen, Δ R H ⊖= Δ R U ⊖+ Δ n g RT , wobei Δ n gdie Änderung der Stoffmenge der an der Reaktion beteiligten Gase bezeichnet. Im vorliegenden Fall ist Δ n g= 10 mol − 12 mol = − 2mol, und wir erhalten

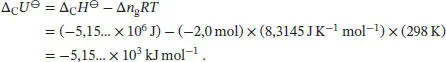
Die Wärmemenge, die im Inneren des Bombenkalorimeters durch die Verbrennung von 120 mg Naphthalin ( M = 128,1632g mol −1) freigesetzt wird, ist

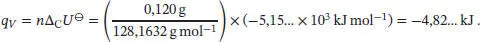
Die Kalorimeterkonstante ist daher

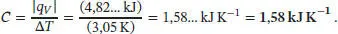
Die Reaktionsgleichung für die Verbrennung von Phenol lautet

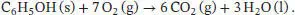
Die Werte entnehmen wir wieder den Tab. 2.10 und 2.11 im Anhang des Lehrbuchs. Mit der gleichen Vorgehensweise wie zuvor erhalten wir Δ C H ⊖= −3054 kJ mol −1, Δ n g = −1 mol und Δ C U ⊖= −3,05… × 10 3kJ mol −1. Die Wärmemenge, die im Inneren des Bombenkalorimeters durch die Verbrennung von 150 mg Phenol ( M = 94,10 g mol −1) freigesetzt wird, ist

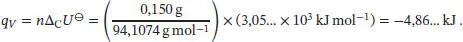
Somit ist der Temperaturanstieg

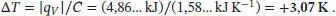
L2.3.5a

1 (i) Reaktion (3) = (−2) × Reaktion (1) + Reaktion (2). Nach dem Satz von Hess werden die Reaktionsenthalpien der Reaktionen ebenso wie die Reaktionsgleichungen kombiniert:ΔRH⊖ hängt mit ΔRU⊖ über die in Gl. (2.20) angegebene Beziehung zusammen, ΔRH⊖=ΔRU⊖ + ΔngRT wobei Δng die Änderung der Stoffmenge der an der Reaktion beteiligten Gase bezeichnet. Im vorliegenden Fall ist Δng = 2 mol + 2 mol − 4 mol − 1 mol = −1 mol, und wir erhalten

2 (ii) Reaktion (1) repräsentiert die Bildung von 2 mol HCl(g) aus den Elementen in ihren jeweiligen Referenzzuständen; die Standardbildungsenthalpie von 1 mol HCl (g) ist daherReaktion (2) repräsentiert die Bildung von 2 mol H2O (g) aus den Elementen in ihren jeweiligen Referenzzuständen; die Standardbildungsenthalpie von 1 mol H2O (g) ist daher

L2.3.6aΔ R H ⊖hängt mit Δ R U ⊖über die in Gl. (2.20) angegebene Beziehung zusammen, Δ R H ⊖=Δ R U ⊖+ Δ n g RT , wobei Δ n gdie Änderung der Stoffmenge der an der Reaktion beteiligten Gase bezeichnet. Im vorliegenden Fall ist Δ n g= 2 mol + 3 mol − 3 mol = +2 mol, und wir erhalten

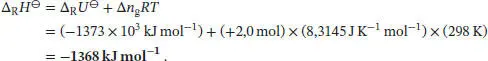
L2.3.7a

1 (i) Die Standardreaktionsenthalpie bei 298 K lässt sich aus den Standardbildungsenthalpien bei 298 K mithilfe von Gl. (2.30a) berechnen:ΔRH⊖ hängt mit ΔRU⊖ über die in Gl. (2.20) angegebene Beziehung zusammen, ΔRH⊖ = ΔRU⊖ + ΔngRT, wobei Δng die Änderung der Stoffmenge der an der Reaktion beteiligten Gase bezeichnet. Im vorliegenden Fall ist Δng = 1 mol + 1 mol − 1 mol = +1 mol, und wir erhalten

2 (ii) Die Differenz der molaren Wärmekapazitäten der Produkte und der Reaktanten lassen sich mithilfe von Gl. (2.32b) und den thermochemischen Daten aus Tab. 2.6 des Lehrbuchs berechnen:Unter der Voraussetzung, dass die Wärmekapazitäten im betrachteten Temperaturbereich konstant sind, können wir die integrierte Form des Kirchhoff’schen Gesetzes (Gl. (2.32d)) anwenden, und wir erhalten:

L2.3.8aDie Reaktionsgleichung C(s, Graphit) + O 2(g) CO (g) repräsentiert die Bildung von CO 2(g) aus den Elementen in ihren jeweiligen Referenzzuständen, daher ist Δ RH ⊖(298 K) = Δ B H ⊖(CO 2. g) = −393,51 kJmol −1. Die Temperaturabhängigkeit der Standardreaktionsenthalpie ist durch das Kirchhoff’sche Gesetz (Gl. (2.32a)) gegeben: