James J. Keeler - Arbeitsbuch zu Atkins, de Paula, Keeler Physikalische Chemie

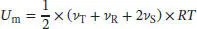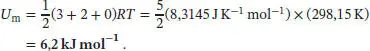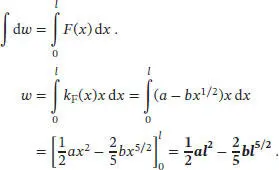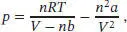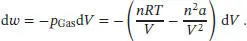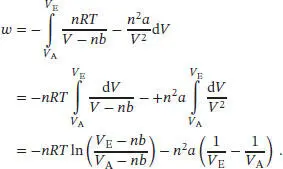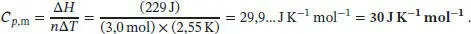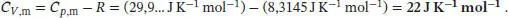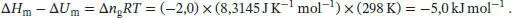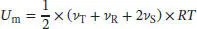
gegeben, wobei v T, v Rund v Sdie Anzahl der Translations-, Rotations- bzw. der Schwingungsfreiheitsgrade des betrachteten Moleküls ist. Jedes der Gasmoleküle kann sich unabhängig in x -, y - und z -Richtung durch den Raum bewegen, daher besitzt es drei Translationsfreiheitsgrade. Kohlendioxid ist ein lineares Molekül, und es besitzt daher zwei Rotationsfreiheitsgrade. Bei Raumtemperatur ist es unwahrscheinlich, dass eine der Schwingungsmoden dieses Moleküls angeregt ist, daher fließen sie nicht in die Berechnung ein ( v S= 0). Für die molare Innere Energie ergibt sich

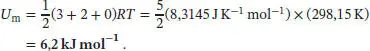
S2.1.3Die benötigte Definition der Arbeit ist durch Gl. (2.4) gegeben, d w = −| F |d z . Integration auf beiden Seiten der Gleichung liefert

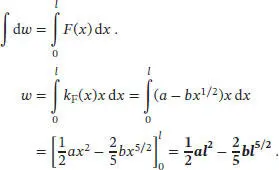
Beachten Sie, dass sich der zweite Term aus dem Verhalten des Elastomers gemäß dem Hooke’schen Gesetz ergibt, wodurch sich der Betrag der insgesamt verrichteten Arbeit reduziert.

S2.1.5

1 (a) Der natürliche Logarithmus lässt sich mithilfe einer Taylor-Reihe entwickeln,Für v ≪ 1 ergibt sich damit näherungsweise ln(1 + v) ≈ v bzw. ln(1 − v) ≈ − v. Daher giltWegen u = n/N folgt

2 (b) Das Hooke’sche Gesetz sagt den Zusammenhang F = Konstante × x voraus; dies bedeutet, dass die Rückstellkraft direkt proportional zur Auslenkung ist. Mithilfe der Beziehung n = x/l können wir für den Ausdruck für die Kraft aus Teilaufgabe (a) auch schreiben:Wir sehen, dass das Hooke’sche Gesetz erfüllt ist, und dass kT/Nl2 eine Kraftkonstante ist.

S2.1.7Die Van-der-Waals-Gleichung ist durch Gl. (1.27b) gegeben,

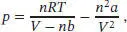
und für die Volumenarbeit gilt laut Gl. (2.6) d w = − p exd V. Bei einer reversiblen Expansion entspricht der äußere Druck pex stets dem Druck des Gases, also gilt

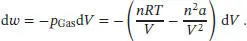
Integration auf beiden Seiten dieser Gleichung liefert

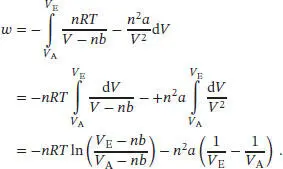
Im Folgenden berechnen wir die verrichtete Arbeit während einer isothermen reversiblen Expansion für die drei in der Aufgabenstellung genannten Fälle; die resultierenden Indikatordiagramme sind in Abb 2.1gemeinsam in einer Darstellung gezeigt.

1 (a) Für ein ideales Gas ergibt sich

2 (b) Schließlich betrachten wir ein Van-der-Waals-Gas, in dem die abstoßenden Kräfte überwiegen. Einsetzen der gegebenen Werte a = 0 und b = 5,11 × 10−2 dm3 mol−1 in den zuvor hergeleiteten, allgemeinen Ausdruck liefert Abb. 2.1

3 (c) Schließlich betrachten wir ein Van-der-Waals-Gas, in dem die anziehenden Kräfte überwiegen. Wir setzen die gegebenen Werte in den zuvor hergeleiteten, allgemeinen Ausdruck ein; hierzu drücken wir die Van-der-Waals-Konstante a in SI-Einheiten aus:

S2.1.9

1 (a) Die Virialgleichung ist durch Gl. (1.25b) gegeben. Die ersten drei Terme lautenEinsetzen von Vm = V / n liefertFolglich ist die verrichtete ArbeitFür n = 1 mol istNach Tab. 1.4 des Lehrbuchs ist B = − 21,7 cm3 mol−1, und aus der Aufgabenstellung ergibt sich C = 1,2 X 103 cm6 mol−2. Damit folgtWir erhalten daher mit Gl. (2.9)

2 (b) Ein ideales Gas entspricht dem ersten Term in der Reihenentwicklung von p. Mit Gl. (2.9) folgt

D2.2.1Der Unterschied resultiert aus der Definition H = U + pV; aus ihr folgt ΔH = ΔU + Δ( pV ). Da Δ(pV) im Allgemeinen nicht null ist (außer für isotherme Prozesse in einem idealen Gas), verschwindet die Differenz zwischen ΔH und ΔU nicht.

Wie in Abschn. 2.2des Lehrbuchs gezeigt wird, kann man ΔH als die Wärme interpretieren, die mit einem Prozess bei konstantem Druck verbunden ist; ΔU ist dann entsprechend die Wärme bei konstantem Volumen. Bei einem Prozess, der bei konstantem Druck abläuft, kann Volumenarbeit verrichtet werden – bei einem Prozess, der bei konstantem Volumen abläuft, hingegen nicht; daher unterscheiden sich die beiden Größen ΔH und ΔU voneinander.

L2.2.1aDie bei konstantem Druck übertragene Wärmemenge entspricht gemäß Gl. (2.18b) der Enthalpieänderung des Systems, q p = ΔH . Der Zusammenhang zwischen der Enthalpieänderung, der Temperaturänderung und der Wärmekapazität ist durch Gl. (2.22b) gegeben; demnach gilt für die molare Wärmekapazität bei konstantem Druck

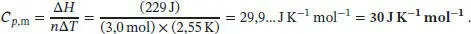
Für ein ideales Gas gilt nach Gl. (2.25) Cp, m– CV , m = R. Somit erhalten wir für die Wärmekapazität bei konstantem Volumen

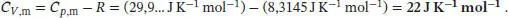
L2.2.2aBei der Ammoniaksynthese werden aus 2 mol der gasförmigen Ausgangsstoffe 4 mol gasförmiges NH 3gebildet. Mithilfe von Gl. (2.19) erhalten wir für die gesuchte Differenz zwischen den molaren Änderungen der Enthalpie und der Inneren Energie

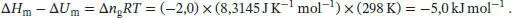
L2.2.3a

1 (i) Die Wärmekapazität bei konstantem Druck kann über die Beziehung Cp = a + bT ausgedrückt werden, wobei a = 20,17 JK−1 und b = 0,3665 JK−2 sein soll. Integration der Beziehung dH = Cp dT liefertWeil der Druck konstant ist, gilt qp = ΔH = +10,7 kJ.Die gegen einen konstanten äußeren Druck pex verrichtete Volumenarbeit ist durch Gl. (2.6) gegeben, w = −pexΔV = − pex(VE − VA). Wenn wir annehmen, dass sich das Gas im mechanischen Gleichgewicht mit der Umgebung befindet, müssen der äußere Druck pex und der Druck des Gases p identisch sein. Das Anfangs- und das Endvolumen des Gases berechnen wir mithilfe der Angaben zu TE und TA gemäß VE = nRTE/p bzw. VA = nRTA/p; es gilt VE − VA = (TE − TA)nR/p. Für die verrichtete Arbeit w und die Änderung der Inneren Energie ΔU erhalten wir

2 (ii) Die Energie und die Enthalpie eines idealen Gases hängen nur von der Temperatur ab (vgl. Abschn. 2.1.2 des Lehrbuchs und Aufgabe L2.1.4a). Daher spielt es keine Rolle, ob sich die Temperatur bei konstantem Volumen oder konstantem Druck ändert. Die Größen ΔH und ΔU sind jeweils gleich, und wie zuvor in Teilaufgabe (a) gilt ΔH = +10,7 kJ und ΔU = +10,1 kJ. Bei konstantem Volumen wird allerdings keine Volumenarbeit verrichtet, und es gilt w = 0. Die übertragene Wärmemenge entspricht daher der Änderung der Inneren Energie, qV = ΔU = +10,1kJ.