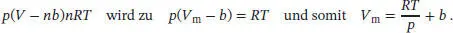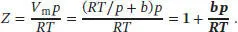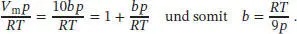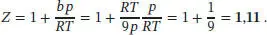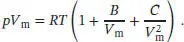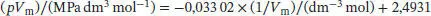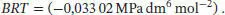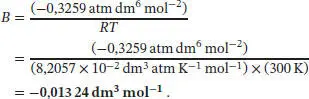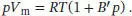
Die Dichte ρ (rho) ist durch m/V gegeben, und für die Masse können wir m = nM schreiben, wobei n die Stoffmenge (in mol) und M die Molmasse ist. Daraus folgt ρ = nM/V = M/V m , wobei V mdas Molvolumen ist. Durch Umstellen erhalten wir V m =M/ρ; daran lässt sich erkennen, dass man aus Messungen der Dichte das molare Volumen bestimmen kann.
Durch Einsetzen des Ausdrucks für das molare Volumen in die Virialgleichung erhalten wir

Die Grenzsteigung einer Auftragung von p/ρ gegen p ist B'RT/M, und damit proportional zu B'; eine solche Auftragung ist in Abb. 1.5gezeigt.
| p /kPa |
ρ /(kg m −3) |
( p / ρ )/(kPa kg −1m 3) |
| 12,22 |
0,225 |
54,32 |
| 25,20 |
0,456 |
55,26 |
| 36,97 |
0,664 |
55,68 |
| 60,37 |
1,062 |
56,85 |
| 85,23 |
1,468 |
58,06 |
| 101,30 |
1,734 |
58,42 |
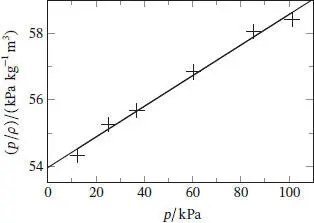
Abb. 1.5
Die Gerade beschreibt die Daten sehr gut; die Geradengleichung lautet
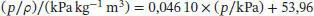
und die Steigung ist
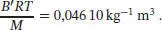
Die Molmasse von Dimethylether (Methoxymethan, CH 3OCH 3), ist M = 2 × 12,01 + 6 × 1,0079 + 16,00 = 46,0674 g mol −1. Mit diesem Wert erhalten wir
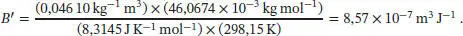
Die Einheiten dieses Ergebnis können wir vereinfachen, indem wir 1 J = 1 kg m 2s −2berücksichtigen, also ist 1 m 3J −1= 1 m kg −1s 2. Beachten Sie, dass 1 Pa = 1 kg m −1s −2ist, daher sind die Einheiten von B' äquivalent zu Pa −1, einem „inversen“ Druck (d. h. dessen Kehrwert):
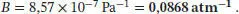
Der Virialkoeffizient B lässt sich mithilfe des Ergebnisses von Aufgabe S1.3.14 des Lehrbuchs bestimmen; die benötigte Beziehung ist B = B'RT :
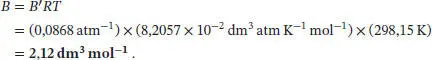
S1.3.17Ein Gas lässt sich nur dann allein durch Erhöhung des Drucks verflüssigen, wenn seine Temperatur unterhalb der kritischen Temperatur liegt; für Stickstoffgas ist dies T krit= 126,3 K.
S1.3.19Der Kompressionsfaktor Z ist in Gl. (1.23) definiert als 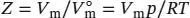 . Wir setzen n = 1 und stellen die gegebene Zustandsgleichung so um, dass wir einen Ausdruck für V merhalten:
. Wir setzen n = 1 und stellen die gegebene Zustandsgleichung so um, dass wir einen Ausdruck für V merhalten:
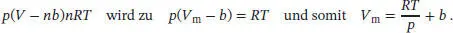
Für den Kompressionsfaktor ergibt sich der Ausdruck
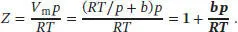
Für V m= 10 b folgt aus der vorangegangenen Gleichung
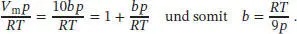
Mithilfe des Ausdrucks für b und Z = 1 + bp/RT können wir nun der Kompressionsfaktor berechnen:
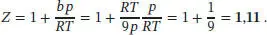
S1.3.21‡Die Virialgleichung in Abhängigkeit vom molaren Volumen (bis zum dritten Term) ist durch Gl. (1.25b) gegeben,
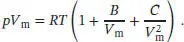
Für Teilaufgabe (a) berücksichtigen wir nur die ersten beiden Terme. Es folgt, dass sich bei einer grafischen Auftragung von pV mgegen 1/ V meine Gerade mit der Steigung BRT ergeben sollte; eine solche Auftragung ist in Abb. 1.6gezeigt.
| p /MPa |
V m/(dm 3mol −1) |
( pV m)/(MPa dm 3mol −1) |
(1/ V m)/(dm −3mol) |
| 0,400 0 |
6,220 8 |
2,488 3 |
0,160 75 |
| 0,500 0 |
4,973 6 |
2,486 8 |
0,201 06 |
| 0,600 0 |
4,142 3 |
2,485 4 |
0,241 41 |
| 0,800 0 |
3,1031 |
2,482 5 |
0,322 26 |
| 1,000 |
2,479 5 |
2,479 5 |
0,403 31 |
| 1,500 |
1,648 3 |
2,472 5 |
0,606 69 |
| 2,000 |
1,232 8 |
2,465 6 |
0,811 16 |
| 2,500 |
0,983 57 |
2,458 9 |
1,016 7 |
| 3,000 |
0,817 46 |
2,452 4 |
1,223 3 |
| 4,000 |
0,609 98 |
2,439 9 |
1,6394 |
Die Werte liegen mit geringer Streuung entlang einer Geraden; die Geradengleichung lautet
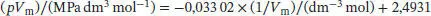
und die Steigung ist
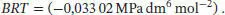
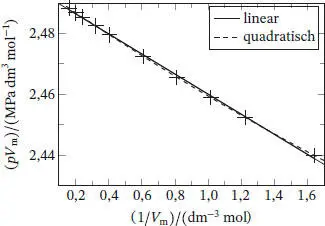
Abb. 1.6
Der Bequemlichkeit halber konvertieren wir den Druck in die Einheit atm, wodurch wir BRT = (−0,3259 atm dm 6mol −2) erhalten; somit ist der zweite Virialkoeffizient
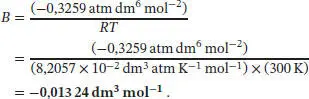
Zur Bearbeitung von Teilaufgabe (b) passen wir die Datenpunkte mithilfe mathematischer Software an ein (quadratisches) Polynom zweiter Ordnung in Bezug auf 1/ Vm an. In Abb. 1.6können wir erkennen, dass die Daten durch eine derartige Funktion (dargestellt als gestichelte Linie) mit noch größerer Präzision beschrieben werden. Das verwendete Polynom lautet
Читать дальше

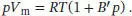


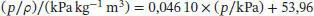
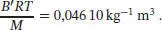
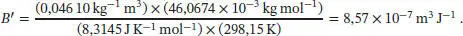
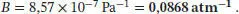
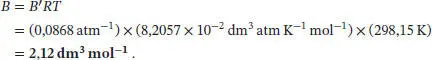
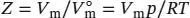 . Wir setzen n = 1 und stellen die gegebene Zustandsgleichung so um, dass wir einen Ausdruck für V merhalten:
. Wir setzen n = 1 und stellen die gegebene Zustandsgleichung so um, dass wir einen Ausdruck für V merhalten: