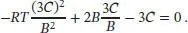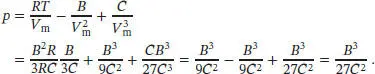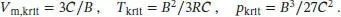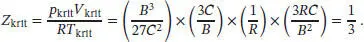Gemäß Tab. 1.7 in Abschn. 1.3.2b des Lehrbuchs ergibt sich der Druck, der durch ein Dieterici-Gas
ausgeübt wird, gemäß
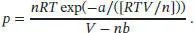
Für den Exponentialterm erhalten wir durch Einsetzen aller bekannten Werte
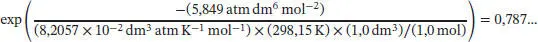
und damit für den Druck
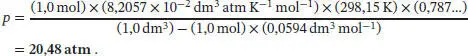
S1.3.11Die Van-der-Waals-Gleichung in Abhängigkeit vom molaren Volumen ist durch Gl. (1.27b) gegeben, 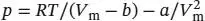 . Multiplikation mit V mauf beiden Seiten der Gleichung liefert
. Multiplikation mit V mauf beiden Seiten der Gleichung liefert
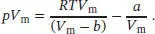
Diesen Ausdruck stellen wir nun um, indem wir den Zähler und den Nenner des ersten Terms durch V mdividieren. Wir erhalten
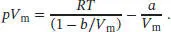
Für die Näherung des Faktors 1/(1 − b/V m) verwenden wir die Reihenentwicklung (1 − x ) −1≈ 1 + x + x 2(wobei wir nach dem zweiten Term abbrechen). So erhalten wir
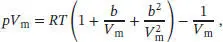
und durch Zusammenfassen der Terme 1/ V mund 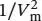
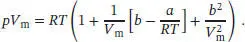
Dieses Ergebnis vergleichen wir nun mit der Virialgleichung in Abhängigkeit vom molaren Volumen, Gl. (1.25b),
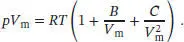
Durch diesen Vergleich erkennen wir, dass für die Virialkoeffizienten
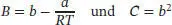
gilt. Aus dem in der Aufgabenstellung gegebenen Wert für C = 1200 cm 6mol −2folgt, dass 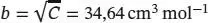 sein muss. In den üblichen Einheiten ausgedrückt ist b = 0,034 64 dm3 mol−1. Der Wert für a lässt sich nun durch Umstellen der Beziehung B = b − a/RT berechnen:
sein muss. In den üblichen Einheiten ausgedrückt ist b = 0,034 64 dm3 mol−1. Der Wert für a lässt sich nun durch Umstellen der Beziehung B = b − a/RT berechnen:
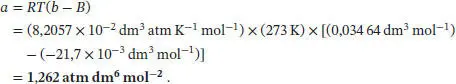
S1.3.13In Abschn. 1.3.2b des Lehrbuchs ist beschrieben, dass kritisches Verhalten mit Schwankungen der Isothermen assoziiert ist, die durch eine bestimmte Zustandsgleichung vorhergesagt werden. Am kritischen Punkt hat die Auftragung des Drucks gegen das Molvolumen einen Wendepunkt mit waagerechter Tangente, und an diesem Punkt gilt
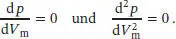
Unser Ansatz besteht darin, zunächst Ausdrücke für die erste und die zweite Ableitung zu finden. Diese setzen wir gleich null, sodass wir zwei Simultangleichungen erhalten, die wir anschließend nach dem kritischen Druck und dem kritischen Volumen auflösen können.

Wenn wir die erste dieser Gleichungen mit 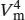 und die zweite mit
und die zweite mit 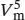 multiplizieren, erhalten wir
multiplizieren, erhalten wir
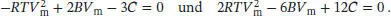
Nun multiplizieren wir die erste Gleichung mit 2 und addieren sie zur zweiten; dadurch eliminieren wir alle Terme, die 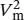 enthalten,
enthalten,
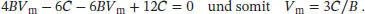
Diesen Ausdruck für V msetzen wir in 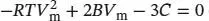 ein, und wir erhalten
ein, und wir erhalten
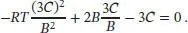
Einer der 3 C -Terme kürzt sich heraus, und wir multiplizieren die gesamte Gleichung mit B 2; so ergibt sich

Den Druck p finden wir, indem wir V m= 3 C/B und T = B 2/3 RC in die vorgeschlagene Zustandsgleichung einsetzen:
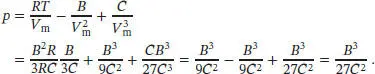
Zusammenfassend schreiben wir für die kritischen Größen
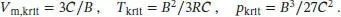
Für den kritischen Kompressionsfaktor Z kritergibt sich mit Gl. (1.29)
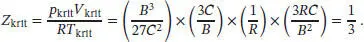
S1.3.15Die Virialgleichung in Abhängigkeit vom Druck (bis zum zweiten Term) ist durch Gl. (1.25a) gegeben,
Читать дальше

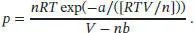
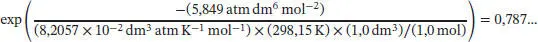
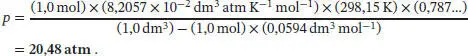
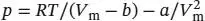 . Multiplikation mit V mauf beiden Seiten der Gleichung liefert
. Multiplikation mit V mauf beiden Seiten der Gleichung liefert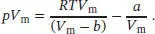
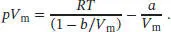
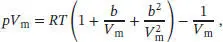
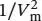
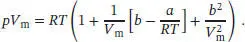
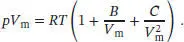
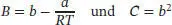
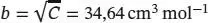 sein muss. In den üblichen Einheiten ausgedrückt ist b = 0,034 64 dm3 mol−1. Der Wert für a lässt sich nun durch Umstellen der Beziehung B = b − a/RT berechnen:
sein muss. In den üblichen Einheiten ausgedrückt ist b = 0,034 64 dm3 mol−1. Der Wert für a lässt sich nun durch Umstellen der Beziehung B = b − a/RT berechnen: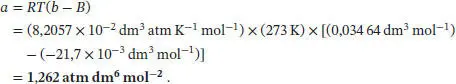
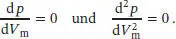

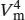 und die zweite mit
und die zweite mit 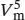 multiplizieren, erhalten wir
multiplizieren, erhalten wir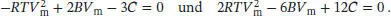
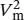 enthalten,
enthalten,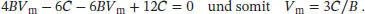
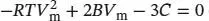 ein, und wir erhalten
ein, und wir erhalten