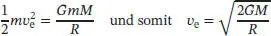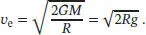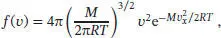1 ...8 9 10 12 13 14 ...43 S1.2.5Die Maxwell’sche Geschwindigkeitsverteilung für dreidimensionale Systeme ist durch Gl. (1.12) gegeben,
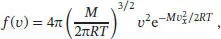
wobei M die Molmasse ist. Die wahrscheinlichste Geschwindigkeit ist durch Gl. (1.18) gegeben, c * = (2 RT/M ) 1/2. Wenn das Intervall der Geschwindigkeiten Δ v eng ist, entspricht der Anteil der Moleküle, deren Geschwindigkeiten in einem Bereich mit dem Zentrum bei c * liegen, in guter Näherung f ( c *)Δ v . Der gesuchte Anteil an Molekülen, deren Geschwindigkeiten in einem Bereich Δ v mit dem Zentrum bei n × c* liegen, ist somit durch
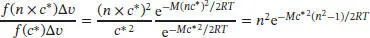
gegeben. Bei der Bildung des Verhältnisses kürzen sich sämtliche Terme in f ( v ) heraus, die Multiplikatoren der Exponentialfunktion sind, mit Ausnahme von v 2. Wenn wir in diesem Ausdruck die Größe c* durch ( 2RT/M ) 1/2ersetzen (d.h., wenn wir Gl. (1.18) einsetzen), erhalten wir schließlich ein übersichtlicheres Ergebnis:
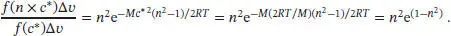
Für n = 3 liefert dieser Ausdruck 3,02× 10−3, und für n = 4 erhalten wir 4,89× 10−6. Anhand dieser Zahlenwerte können wir erkennen, dass nur sehr wenige Moleküle ein Vielfaches der wahrscheinlichsten Geschwindigkeit c* besitzen.
S1.2.7Damit ein Objekt (egal, ob es sich um ein Raumschiff oder um ein Molekül handelt) die Gravitation der Erde überwinden kann, muss es eine hinreichend große kinetische Energie besitzen; der Betrag der Energie muss mindestens der gravitationsbedingten potenziellen Energie des Objektes an der Erdoberfläche entsprechen. Das Gravitationspotenzial zwischen zwei Objekten mit den Massen m 1und m 2, die sich im Abstand r zueinander befinden, ist
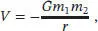
wobei G die (universelle) Gravitationskonstante ist. Für ein Objekt mit der Masse m an der Erdoberfläche ist das Gravitationspotenzial durch
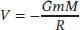
gegeben, wobei wir hier mit M die Masse der Erde und mit R den Radius unseres Planeten bezeichnen. Anhand dieses Ausdrucks können wir erkennen, dass das Potenzial an der Erdoberfläche gleich groß ist wie im imaginären Fall, wenn die Masse der Erde an einem Punkt im Abstand ihres Radius konzentriert wäre.
Während sich eine Masse von der Erdoberfläche entfernt, nimmt ihre potenzielle Energie stetig zu, d. h. sie wird weniger negativ; bei sehr großen Distanzen geht sie schließlich gegen null. Diese Änderung der potenziellen Energie muss vollständig in kinetische Energie umgewandelt werden, damit eine Masse die Gravitation überwinden kann. Eine Masse m , die sich mit der Geschwindigkeit v bewegt, besitzt die kinetische Energie 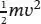 ; diese Geschwindigkeit entspricht der Fluchtgeschwindigkeit v ewenn
; diese Geschwindigkeit entspricht der Fluchtgeschwindigkeit v ewenn
(G1.4) 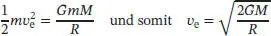
gilt. Der Term unter der Quadratwurzel hängt folgendermaßen mit der Beschleunigung des freien Falls, g , zusammen: Eine Masse m an der Erdoberfläche erfährt aufgrund der Gravitation eine Kraft , die GMm/R 2entspricht. (Beachten Sie, dass diese Kraft proportional zu R −2ist.) Diese Kraft beschleunigt die Masse in Richtung Erdoberfläche, und wir schreiben dafür (wie gewohnt) F = mg. Wenn wir die beiden Ausdrücke für die Kraft gleichsetzen, erhalten wir

Wenn wir nun den Ausdruck für GM/R in die Beziehung für v eeinsetzen, erhalten wir
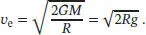
Wir sehen, dass die Fluchtgeschwindigkeit v esowohl eine Funktion des Erdradius fi als auch der Beschleunigung des freien Falls g ist.
1 (a) Der Radius der Erde ist 6,37 × 106 m und g = 9,81 m s−2, daher ist die Fluchtgeschwindigkeit
2 (b) Für den Mars wird in der Aufgabenstellung keine Angabe zur Beschleunigung des freien Falls gemacht; allerdings folgt aus Gl. (G1.4), dass g = GM/R2 gilt, und somitDie Beschleunigung des freien Falls auf dem Mars können wir daher aus den übrigen Angaben berechnen:Für Fluchtgeschwindigkeit auf dem Mars erhalten wir daherDie mittlere Geschwindigkeit von Molekülen ist durch Gl. (1.17), , gegeben. Diesen Ausdruck können wir geeignet umstellen, um die Temperatur zu erhalten, bei der die mittlere Geschwindigkeit der Moleküle gerade der Fluchtgeschwindigkeit ve entspricht:Für H2-Moleküle auf der Erde liefert diese GleichungIn der folgenden Tabelle sind die Ergebnisse für alle drei in der Aufgabenstellung genannten Gase auf beiden Planeten aufgelistet.Planetve/ms−1T/104K(H2)T/104 K (He)T /104K(O2)Erde1,12 × 1041,192,3618,9Mars5,04 × 1030,2420,4813,84Der Anteil der Moleküle, die sich mit größeren Geschwindigkeiten als der Fluchtgeschwindigkeit bewegen, lässt sich aus der Maxwell-Boltzmann-Verteilung durch Integration zwischen ve und ∞ ermitteln:Dieses Integral lässt sich am einfachsten unter Zuhilfenahme mathematischer Software lösen. In der folgenden Tabelle sind die Ergebnisse für die Anteile F für die drei genannten Gasmoleküle aufgelistet; ein Eintrag von null bedeutet, dass der Anteil innerhalb der Genauigkeit dieser automatisierten Berechnung gleich null ist.PlanetT/KF (H2)F (He)F (O2)Erde240000—15001,49 × 10−49,52 × 10−90Mars2401,12 × 10−55,09 × 10−110—15000,0254,31 × 10−24,61 × 10−14Diese Ergebnisse zeigen, dass leichtere Moleküle grundsätzlich eine größere Wahrscheinlichkeit besitzen, die Atmosphäre zu verlassen (denn sie bewegen sich im Mittel schneller); außerdem erkennen wir, dass eine Temperaturerhöhung diese Wahrscheinlichkeit erhöht (denn dadurch erhöht sich auch die mittlere Geschwindigkeit der Moleküle). Aufgrund der geringeren Fluchtgeschwindigkeit ist es für leichte Moleküle einfacher, die Atmosphäre des Planeten Mars zu verlassen als die Erdatmosphäre, und für schwerere Moleküle ist es nahezu unmöglich, den Gravitationsbereich der Erde zu verlassen.
S1.2.9Die Maxwell’sche Geschwindigkeitsverteilung für dreidimensionale Systeme ist durch Gl. (1.12) gegeben,
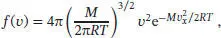
wobei M die Molmasse ist. Der Anteil der Moleküle, die sich mit Geschwindigkeiten zwischen v 1und v 2bewegen, lässt sich aus der Maxwell-Boltzmann-Verteilung durch Integration zwischen diesen beiden Geschwindigkeiten ermitteln (der Einsatz mathematischer Software ist dabei hilfreich):
Читать дальше

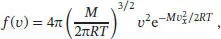
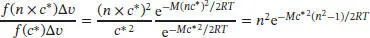
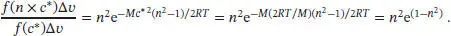
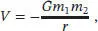
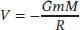
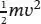 ; diese Geschwindigkeit entspricht der Fluchtgeschwindigkeit v ewenn
; diese Geschwindigkeit entspricht der Fluchtgeschwindigkeit v ewenn