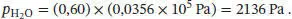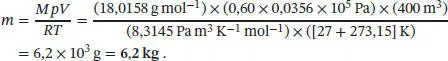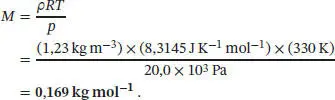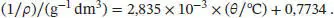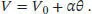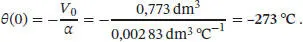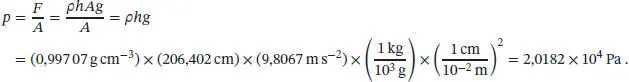Der Partialdruck des Wasserdampfs in dem Raum beträgt 60 % des Gleichgewichtsdampfdrucks, den wir aus einem Nachschlagewerk wie dem CRC Handbook of Chemistry and Physics oder ähnlichen Quellen entnehmen können,
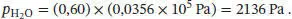
Durch Einsetzen der Gleichung für die Stoffmenge n = m / M in die Zustandsgleichung des idealen Gases erhalten wir pV = mRT / M und nach Umstellen m = MpV / RT . Damit ist
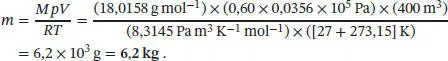
L1.1.8a
1 (i) Der Einfachheit halber nehmen wir an, das Volumen des Behälters betrage 1 m3. Dann ist die gesamte Masse (G1.1)Wenn wir Luft als ideales Gas ansehen, ist pGV = nGRT, wenn nG die gesamte Stoffmenge des Gases ist, (G1.2)Die Gln. (G1.1)und (G1.2)für die Stoffmengen der Gase müssen gleichzeitig erfüllt sein. Wenn wir nO2 aus Gl. (G1.1)in Gl. (G1.2)einsetzen, erhalten wirDie Stoffmengenanteile (Molenbrüche) sindDie Partialdrücke sind pN2 = (0,762) × (0,987 bar) = 0,752 bar und pO2 = (0,238) × (0,987 bar) = 0,235 bar. Zur Kontrolle berechnen wir deren Summe: (0,752 + 0,235) bar = 0,987 bar.
2 (ii) Diese Teilaufgabe ist am einfachsten zu lösen, wenn man sich klar macht, dass nG, pG und mG als experimentell bestimmte Größen dieselben Werte haben wie in Teilaufgabe (i). Allerdings sind die zu lösenden Gleichungen für die Stoffmengen, die Molenbrüche und die Partialdrücke etwas verändert:(G1.1’)(G1.2’)Wegen xAr = 0,0100 ist nAr = 0,396 mol und daherundDurch Lösen dieser Gleichung erhalten wirDie Partialdrücke sind
L1.1.9aWir nehmen an, dass die Zustandsgleichung des idealen Gases ( Gl. (1.4)) gilt, pV = nRT. Die Aufgabe besteht nun darin, die gegebene Dichte mit der Molmasse der Verbindung in Beziehung zu setzen.
Zunächst drücken wir die Stoffmenge n über die Masse m geteilt durch die Molmasse M aus, pV = ( m / M ) RT; nach Division durch V auf beiden Seiten der Gleichung erhalten wir p = ( m / V )( RT / M ). Die Größe ( m / V ) entspricht der Dichte ρ, also gilt p = ρRT / M , was sich umstellen lässt zu M = ρRT / p ; dies ist die gesuchte Beziehung zwischen der Molmasse M und der Dichte ρ .
Einsetzen der Werte ergibt
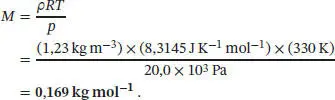
Dabei haben wir 1 J = 1 kg m 2s −2und 1 Pa = 1 kg m −1s −2verwendet.
L1.1.10aDas Gesetz von Charles, Gl. (1.3b), besagt: Bei konstanter Stoffmenge n und konstantem Druck p gilt V ∝ T , und bei konstanter Stoffmenge n und konstantem Volumen V gilt p ∝ T . Für eine bestimmte vorgegebene Stoffmenge ist die Dichte ρ proportional zu 1/ V , und es folgt 1/ ρ ∝ T . Am absoluten Nullpunkt der Temperatur geht V → 0, daher geht ρ → ∞ und somit 1/ ρ → 0.
Die Aufgabe ist am einfachsten zu lösen, wenn man eine Probe mit einer geeigneten Masse wählt, z. B. 1,000 g, und dann das Volumen bei jeder Temperatur berechnet. Anschließend trägt man das Volumen gegen die Temperatur (in °C) auf und extrapoliert auf V = 0. Es ergibt sich folgende Tabelle:
| θ /°C |
ρ /(g dm −3) |
(1/ ρ )/(g −1dm 3) |
| −85 |
1,877 |
0,5328 |
| 0 |
1,294 |
0,7728 |
| 100 |
0,946 |
1,0571 |
In Abb. 1.1ist die grafische Auftragung von 1/ ρ als Funktion von θ gezeigt. Die Extrapolation ergibt für den absoluten Nullpunkt einen Wert nahe −273 °C. Die Gleichung der Ausgleichsgeraden ist
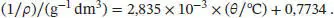
Den Achsenabschnitt bei 1/ ρ = 0 finden wir durch Lösen der Gleichung

Daraus folgt für den absoluten Nullpunkt θ = −273 °C.
Alternativ könnte man eine Gleichung für V als lineare Funktion von θ verwenden (die in Abb. 1.1eingezeichnete Ausgleichsgerade, die nichts anderes ist als das Gesetz von Charles),
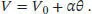
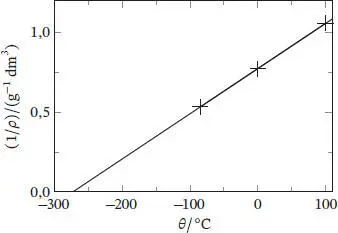
Abb. 1.1
Am absoluten Nullpunkt ist V = 0 und
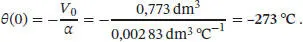
L1.1.11aDie gesamte Stoffmenge ist n = n (H 2) + n (N 2) = 2,0 mol + 1,0 mol = 3,0 mol; nach Gl. (1.7) gilt für den Molenbruch x J= n J/ n .
1 (i) Die Molenbrüche sind
2 (ii) Wir nehmen an, dass die Zustandsgleichung idealer Gase ( Gl. 1.4) für jede der Einzelkomponenten sowie für die Mischung als Ganzes gilt. Dann ist pJ = nJRT/V und somit
3 (iii) Der Gesamtdruck istoder 3,00 atm.
Beachten Sie, dass 1 mol bei Standardbedingungen (STP) ein Volumen von 22,4 dm 3einnimmt, wie in der obigen Gleichung angegeben. Da insgesamt 3,0 mol vorliegen, muss der Gesamtdruck daher 3,0 atm sein.
Zusatzfrage: Gilt das Dalton’sche Gesetz auch für eine Mischung von Gasen, die der Van-der-Waals-Gleichung gehorchen?
S1.1.1
1 (a) Der Ausdruck ρgh liefert den Druck in der Apparatur in der Einheit Pascal (Pa), wenn die verwendeten Größen in SI-Einheiten angegeben werden. Daher ist es hilfreich, die Drücke in die EinheitPa umzurechnen. Die angegebene Dichte von Quecksilber entsprichtDaraus folgt, mit 760 Torr = 1 atm = 1,013 25 × 105 Pa,
2 (b) Wir bringen die Zustandsgleichung des idealen Gases ( Gl. (1.4)) in die Form R = pV/nT. Alle Größen auf der rechten Seite dieser Gleichung sind messbar:
Der Gasdruck ergibt sich aus der Kraft pro Flächeneinheit, die eine Wassersäule der Höhe 206,402 cm aufgrund ihres Gewichts auf das Gas ausübt. Das Manometer soll überall dieselbe Querschnittsfläche A haben. Die Kraft ist F = mg ; dabei ist m die Masse der Wassersäule und g die Beschleunigung des freien Falls. Für die Masse der Wassersäule gilt m = ρV = ρhA mit h = 206,402 cm und der Querschnittsfläche A . Es folgt
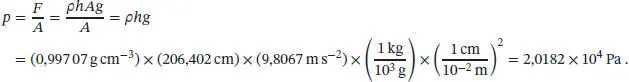
Damit erhalten wir
Читать дальше