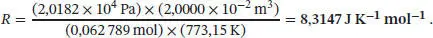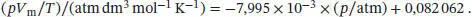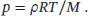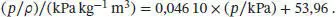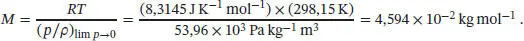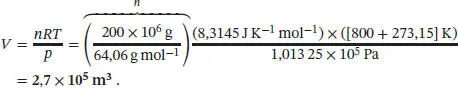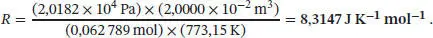
Der Literaturwert ist R = 8,3145 J K −1mol −1. Eigentlich müsste man die Gasvolumina auf den Druck p = 0 extrapolieren, um den bestmöglichen Wert von R zu erhalten. Bei den gegebenen Bedingungen verhält sich Helium jedoch bereits nahezu wie ein ideales Gas, sodass der für R ermittelte Wert recht nahe beim Literaturwert liegt.
S1.1.3Aus der Zustandsgleichung des idealen Gases, pV = nRT , ergibt sich pV m= RT , wobei V mdas molare Volumen ist (also das Volumen für n = 1 mol). Durch Umstellen erhalten wir p = RT / V m, so dass eine Auftragung von p gegen T / V meine Gerade mit der Steigung R ergeben sollte.
Reale Gase verhalten sich jedoch nur bei einem Druck von null ideal, daher müssen wir die Daten auf einen Druckwert von null extrapolieren. Eine Herangehensweise ist, die Zustandsgleichung des idealen Gases in die Form pV m/ T = R zu bringen und zu erkennen, dass der Term pV m/ T für ein reales Gas bei einem Druck von null gegen R geht. Daher kann aus dem Achsenabschnitt einer Auftragung von pV m/ T gegen p bei p = 0 näherungsweise ein Wert für R erhalten werden. Damit die Extrapolation der Ausgleichsgeraden auf den Punkt bei p = 0 verlässlich ist, müssen die Datenpunkte hinreichend präzise auf einer geraden Linie liegen. Die Auftragung der angegebenen Werte ist in Abb. 1.2gezeigt.
| p /atm |
V m/(dm 3mol −1) |
( pV m/ T )/(atm dm 3mol −1K −1) |
| 0,750 000 |
29,8649 |
0,082 0014 |
| 0,500 000 |
44,809 0 |
0,082 022 7 |
| 0,250 000 |
89,638 4 |
0,082 0414 |
Die Datenpunkte liegen nahe einer Ausgleichsgeraden mit der Gleichung
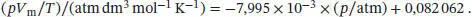
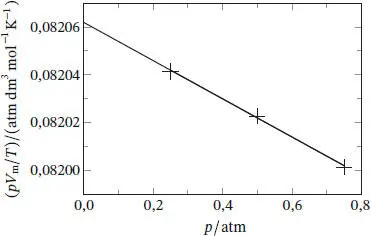
Abb. 1.2
Aus dem Achsenabschnitt erhalten wir für R den Wert 0,082 062 atm dm 3mol −1K −1. Die Daten sind mit sechs signifikanten Stellen angegeben; die Punkte liegen jedoch nicht besonders präzise auf der Ausgleichsgeraden, so dass der Wert für R hier mit einer signifikanten Stelle weniger angegeben wurde.
S1.1.5Für ein ideales Gas gilt pV = nRT , was sich umstellen lässt zu p = nRT/V . Die Stoffmenge in Mol ergibt sich aus n = m/M, wobei M die Molmasse und m die Masse des Gases ist. Daher gilt p = (m/M)(RT/V). Die Größe m / V entspricht der Dichte ρ , und somit gilt
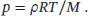
Daraus folgt, dass p/ρ für ein ideales Gas für jede beliebige Temperatur konstant sein sollte. Reale Gase nähern sich für p → 0 diesem Wert an. Eine geeignete Auftragung ist p/ρ gegen p; aus dem Achsenabschnitt bei p = 0 erhalten wir in guter Näherung den Wert von RT/M. In Abb. 1.3ist diese grafische Auftragung für die gegebenen Werte gezeigt.
| p /kPa |
ρ/(kg m −3) |
( p /ρ)/(kPa kg −1m 3) |
| 12,22 |
0,225 |
54,32 |
| 25,20 |
0,456 |
55,26 |
| 36,97 |
0,664 |
55,68 |
| 60,37 |
1,062 |
56,85 |
| 85,23 |
1,468 |
58,06 |
| 101,30 |
1,734 |
58,42 |
Die Datenpunkte liegen nahe einer Ausgleichsgeraden mit der Gleichung
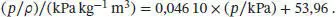
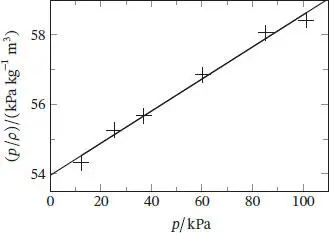
Abb. 1.3
Der Achsenabschnitt ist ( p / ρ ) lim p→0und entspricht RT/M . Nun können wir die molare Masse berechnen:
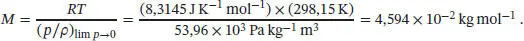
Die Molmasse von Dimethylether ist also näherungsweise 45,94 g mol−1.
S1.1.7
1 (a) Für ein ideales Gas gilt pV = nRT ( Gl. (1.4)), und daher für eine Probe bei konstantem Volumen und konstanter Temperatur p1/T1 = p2/T2. Wenn der Druck um Δp und die Temperatur um ΔT erhöht werden, folgt mit p2 = p1 + Δp und T2 = T1 + ΔTFür eine Temperaturänderung um 1,00 K ist ΔT = 1,00 K, und somit gilt am Tripelpunkt von WasserAlternativ können wir für die Druckänderung mit der Temperatur auch schreiben:
2 (b) Eine Temperatur von 100,00 °C entspricht einer Temperaturerhöhung ausgehend vom Tripelpunkt um 100,00 + 273,15 − 273,16 = 99,99 K, und somit einer Druckänderung vonDer Enddruck ist daher 6,69 + 2,44… = 9,14 kPa.
3 (c) Für ein ideales Gas ist das Verhältnis Δp/ΔT von der Temperatur unabhängig; daher führt eine Temperaturerhöhung um 1,00 K ausgehend von 100,00 °C zu einer Druckerhöhung von 24,5 Pa, wie wir in Teilaufgabe (a) bereits gezeigt haben.
S1.1.9Die Molmasse von Schwefeldioxid ist M (SO 2) = 32,06 g mol −1+ 2 × 16,00 g mol −1= 64,06 g mol −1. Wenn wir annehmen, dass sich das Gas ideal verhält, können wir das Volumen mithilfe der Zustandsgleichung des idealen Gases ( Gl. (1.4), pV = nRT ) bei einem angenommenen Ausstoß von 200 t (also 200 × 10 3kg) berechnen:
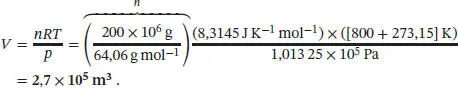
(Beachten Sie, dass wir für die Berechnung die in der Einheit Tonnen (t) angegebene Masse in die Einheit Gramm (g) umgerechnet haben.) Eine Wiederholung der Berechnung für einen angenommenen Ausstoß von 300 t liefert ein Volumen von 4, 1× 105 m3.
Das Volumen des freigesetzten Gases liegt also zwischen 0,27 km3und 0,41 km3.
S1.1.11‡Wir betrachten eine Atmosphärensäule mit der Querschnittsfläche A Der Druck p in einer beliebigen Höhe entspricht der abwärts gerichteten Kraft, die auf diese Fläche wirkt; Ursache für diese Kraft ist die gravitationsbedingte Anziehung der Gasmoleküle, die sich oberhalb der vorgegebenen Höhe befinden – vereinfachend gesagt das „Gewicht“ der Luft.
Nun nehmen wir an, dass die Höhe h um d h ansteigt. Die Kraft, die auf die Fläche A wirkt, wird dadurch verringert – denn direkt oberhalb davon liegt nun ein kleinerer Teil der Atmosphäre. Genauer gesagt verringert sich die Kraft um den Betrag, den ein gasgefüllter Zylinder mit der Querschnittsfläche A und der Höhe d h aufgrund der Gravitation ausübt. Wenn ρ die Dichte des Gases ist, ergibt sich die Masse des Gases innerhalb des Zylinders gemäß ρ × A d h ; die Kraft, die durch diese Masse ausgeübt wird, entspricht ρgA d h , wobei g die Beschleunigung des freien Falls ist. Die Druckänderung d p , die sich aus einem Anstieg der Höhe um d h ergibt, entspricht dieser Kraft geteilt durch die Fläche, sodass folgt:
Читать дальше